
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модель размещения розничной торговой сети
|
|
Спрос на различные товары зависит от населения, товары в магазины поставляют со складов. Необходимо разместить торговые магазины так, чтобы общие затраты на строительство, эксплуатацию, транспортировку продукции и потери от некачественного обслуживания покупателей были наименьшими.
Введем обозначения:
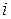 - номер склада (базы);
- номер склада (базы);
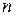 - число всех складов (баз);
- число всех складов (баз);
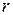 - вид товара;
- вид товара;
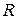 - число всех видов товара;
- число всех видов товара;
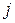 - номер торговой точки (магазина);
- номер торговой точки (магазина);
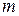 - число торговых точек;
- число торговых точек;
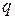 - номер варианта развития торговой точки;
- номер варианта развития торговой точки;
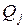 - число возможных вариантов развития
- число возможных вариантов развития 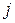 -й торговой точки;
-й торговой точки;
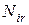 - количество
- количество 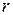 -го вида товара на
-го вида товара на 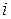 -м складе;
-м складе;
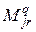 - количество реализуемой продукции
- количество реализуемой продукции 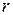 -го вида в
-го вида в 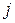 -й торговой точке согласно
-й торговой точке согласно 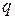 -му варианту;
-му варианту;
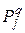 - приведенные затраты
- приведенные затраты 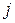 -й торговой точки согласно
-й торговой точки согласно 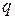 -му варианту;
-му варианту;
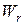 - объем продукции
- объем продукции 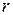 -го вида, потребляемой во всей торговой сети;
-го вида, потребляемой во всей торговой сети;
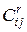 - стоимость перевозки единицы продукции
- стоимость перевозки единицы продукции 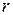 - го вида от
- го вида от 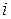 - го склада к
- го склада к 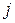 -й торговой точке;
-й торговой точке;
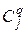 - потери за счет затрат времени покупателей (некачественного обслуживания) в
- потери за счет затрат времени покупателей (некачественного обслуживания) в 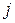 -й торговой точке, развивающейся согласно
-й торговой точке, развивающейся согласно 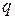 -му варианту;
-му варианту;
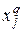 - искомая величина, равная 1, если в
- искомая величина, равная 1, если в 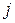 -й торговой точке выбирается
-й торговой точке выбирается 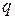 -й вариант, и равная 0 в противном случае;
-й вариант, и равная 0 в противном случае;
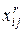 - объем перевозки
- объем перевозки 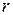 -й продукции из
-й продукции из 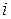 -го склада в
-го склада в 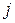 -ю торговую точку.
-ю торговую точку.
В этой модели размещения розничной торговой сети требуется найти такие 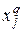 и
и 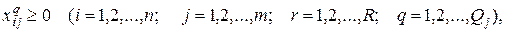 при которых достигается минимум совокупных затрат и потерь
при которых достигается минимум совокупных затрат и потерь
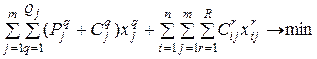
и выполняются условия:
· вывоз товаров из складов должен быть в пределах возможного
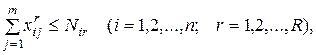

· поставляемые товары должны соответствовать мощностям торговых точек
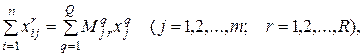
· объем поставляемой продукции должен соответствовать потреблению
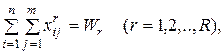
· должен быть выбран только один вариант развития торговой точки
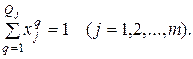
Решая полученную задачу, получаем оптимальные варианты развития торговых точек 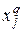 и транспортные потоки
и транспортные потоки 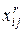 , т.е. получаем оптимальное размещение розничной торговой сети.
, т.е. получаем оптимальное размещение розничной торговой сети.
Заметим, что потери покупателей 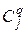 могут рассчитываться в стоимостном выражении. Например,
могут рассчитываться в стоимостном выражении. Например, 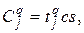 где
где 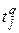 - средние потери времени в часах одним покупателем за счет простаивания в очереди и покупки товара в
- средние потери времени в часах одним покупателем за счет простаивания в очереди и покупки товара в 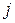 -м магазине, развивающемся согласно
-м магазине, развивающемся согласно 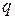 -му варианту;
-му варианту; 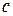 - средняя заработная плата одного человека за один час;
- средняя заработная плата одного человека за один час; 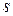 - среднее число покупателей в
- среднее число покупателей в 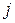 -м магазине.
-м магазине.
Модель планирования деятельности торгового предприятия
На основании изучения спроса покупателей торговое предприятие разрабатывает месячные, квартальные и годовые планы своей хозяйственной деятельности. При этом следует учитывать возможность увеличения прибыли предприятия, выполнение плана товарооборота, полного удовлетворения спроса покупателей на различные виды товаров и качество обслуживания. Другими словами, в плане торгового предприятия должны быть отражены способы наилучшего использования имеющихся ресурсов: торговые залы, складские помещения, численность персонала, торговое оборудование и т.д.
Введем обозначения
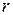 - вид товарной группы;
- вид товарной группы;
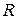 - число всех видов товарных групп;
- число всех видов товарных групп;
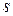 - вид товара, реализуемого в магазине;
- вид товара, реализуемого в магазине;
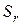 - число видов товара в
- число видов товара в 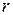 -й товарной группе;
-й товарной группе;
 - нижняя и верхняя границы товарооборота для магазина;
- нижняя и верхняя границы товарооборота для магазина;
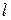 - вид трудовых ресурсов, используемых в магазине;
- вид трудовых ресурсов, используемых в магазине;
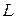 - число всех видов трудовых ресурсов;
- число всех видов трудовых ресурсов;
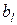 - время, которое могут работать продавцы
- время, которое могут работать продавцы 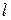 -й квалификации в данном магазине;
-й квалификации в данном магазине;
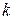 - вид имеющихся в магазине площадей (торговые залы, подсобные помещения и др.);
- вид имеющихся в магазине площадей (торговые залы, подсобные помещения и др.);
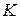 - число всех видов площадей;
- число всех видов площадей;
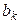 - наличные в магазине площади
- наличные в магазине площади 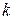 -го вида;
-го вида;
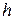 - вид издержек обращения в денежном выражении;
- вид издержек обращения в денежном выражении;
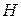 - число всех видов обращения;
- число всех видов обращения;
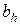 - объем издержек обращения в денежном выражении;
- объем издержек обращения в денежном выражении;
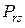 - прибыль магазина от реализации единицы товара
- прибыль магазина от реализации единицы товара 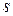 -го вида из
-го вида из 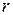 -й группы товаров;
-й группы товаров;
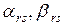 - нижний и верхний пределы по реализации
- нижний и верхний пределы по реализации 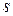 -го вида товара из
-го вида товара из 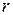 -й группы товаров;
-й группы товаров;
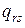 - средняя розничная цена
- средняя розничная цена 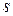 -го вида товара из
-го вида товара из 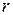 -й группы товаров;
-й группы товаров;
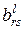 - норма расхода времени на продажу товара
- норма расхода времени на продажу товара 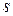 -го вида из
-го вида из 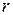 -й группы;
-й группы;
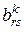 - норма площади
- норма площади 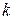 -го вида, необходимой для осуществления продажи единицы товара
-го вида, необходимой для осуществления продажи единицы товара 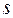 -го вида из
-го вида из 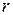 -й группы;
-й группы;
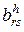 - норма расхода
- норма расхода 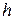 -го вида издержек обращения в денежном выражении при реализации единицы
-го вида издержек обращения в денежном выражении при реализации единицы 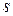 -го вида товара из
-го вида товара из 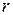 -й группы;
-й группы;
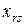 - искомый объем продажи
- искомый объем продажи 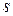 -го вида товаров из
-го вида товаров из 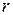 -й группы.
-й группы.
Тогда модель планирования хозяйственной деятельности предприятия состоит в определении таких 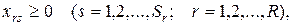 при которых достигается максимальная прибыль
при которых достигается максимальная прибыль
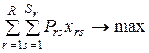
и выполняются ограничения:
· по имеющимся трудовым ресурсам 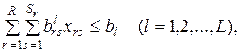
· по имеющимся видам площадей 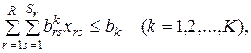
· по имеющимся видам издержек обращения 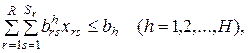
· по объему товарооборота 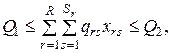
· по выполнению плана ассортимента товаров 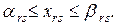
Решая полученную модель как задачу линейного программирования, получаем оптимальный план реализации товаров 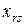 и товарооборота
и товарооборота 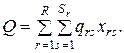 Прибыль торгового предприятия равна разности между валовым доходом и издержками обращения. Валовый доход может измеряться суммой торговых скидок, составляющих определенный процент от различной цены товара, т.е. прибыль
Прибыль торгового предприятия равна разности между валовым доходом и издержками обращения. Валовый доход может измеряться суммой торговых скидок, составляющих определенный процент от различной цены товара, т.е. прибыль 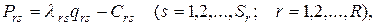
где 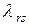 - торговая скидка;
- торговая скидка; 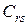 - суммарные издержки обращения на единицу
- суммарные издержки обращения на единицу 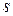 -го вида товара из
-го вида товара из 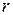 -й группы.
-й группы.
В модели планирования хозяйственной деятельности предприятия можно использовать критерий товарооборота с учетом ограничений на ресурсы и ассортимент реализуемых товаров.
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления A 1, A 2,..., Аm в n пунктов назначения В 1, В 2,..., Вn. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки [1, 14].
Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через cij тарифы перевозки единицы груза из i -го пункта отправления в j -й пункт назначения, через аi - запасы груза в i -м пункте отправления, через bj - потребности в грузе в j -м пункте назначения, а через хij - количество единиц груза, перевозимого из i -го пункта отправления в j -й пункт назначения.
Тогда математическая постановка задачи состоит в определении минимального значения функции
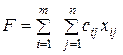 (6.5)
(6.5)
при условиях
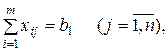 (6.6)
(6.6)
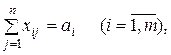 (6.7)
(6.7)
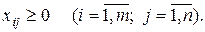 (6.8)
(6.8)
Поскольку переменные  удовлетворяют системам линейных уравнений (6.6) и (6.7) и условию неотрицательности (6.8), то обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.
удовлетворяют системам линейных уравнений (6.6) и (6.7) и условию неотрицательности (6.8), то обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.
Всякое неотрицательное решение систем линейных уравнений (6.6) и (6.7), определяемое матрицей 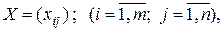 называется планом транспортной задачи.
называется планом транспортной задачи.
План 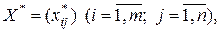 при котором функция (6.5) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
при котором функция (6.5) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
Обычно исходные данные задачи записывают в виде табл.6.1.
Таблица 6.1
Исходные данные транспортной задачи
| Пункты отправления | Пункты назначения | Запасы | ||||
| B 1 | … | Bj | … | Bn | ||
| A 1 | c 11 x 11 | … | c 1 j x 1 j | … | c 1 n x 1 n | a 1 |
| … | … | … | … | … | … | … |
| Ai | ci1 xi 1 | … | cij xij | … | cin xin | ai |
| … | … | … | … | … | … | … |
| Am | cm 1 xm 1 | … | cmj xmj | … | cmn xmn | am |
| Потребности | b 1 | … | bj | … | bn |
Общее наличие груза у поставщиков равно 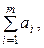 а общая потребность в грузе в пунктах назначения равна
а общая потребность в грузе в пунктах назначения равна 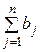 единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.
единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.
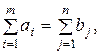 (6.9)
(6.9)
то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.
Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т.е. чтобы выполнялось равенство (6.9).
В случае превышения запаса над потребностью (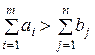 ) вводится фиктивный (n +1)-й пункт назначения с потребностью
) вводится фиктивный (n +1)-й пункт назначения с потребностью 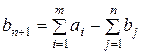 и соответствующие тарифы считаются равными нулю:
и соответствующие тарифы считаются равными нулю: 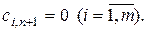 Полученная задача является транспортной задачей, для которой выполняется равенство (6.9).
Полученная задача является транспортной задачей, для которой выполняется равенство (6.9).
Аналогично, при 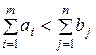 , вводится фиктивный (m +1)-й пункт отправления с запасом груза
, вводится фиктивный (m +1)-й пункт отправления с запасом груза 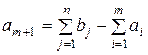 и тарифы полагаются равными нулю:
и тарифы полагаются равными нулю: 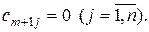
Этим задача сводится к обычной транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи.
В дальнейшем будем рассматривать закрытую модель транспортной задачи. Если же модель конкретной задачи является открытой, то, исходя из сказанного выше, перепишем таблицу условий задачи так, чтобы выполнялось равенство (6.9).
Число переменных xij в транспортной задаче с m пунктами отправления и n пунктами назначения равно nm, а число уравнений в системах (6.6) и (6.7) равно n + m. Так как мы предполагаем, что выполняется условие (6.9), то число линейно независимых уравнений равно n + m - 1. Следовательно, опорный план транспортной задачи может иметь не более n + m - 1 отличных от нуля неизвестных.
Если в опорном плане число отличных от нуля компонент равно в точности n + m - 1, то план является невырожденным, а если меньше - то вырожденным.
Для определения опорного плана существует несколько методов: метод северо-западного угла, метод минимального элемента, метод аппроксимации Фогеля и др. Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом.
Для определения оптимального плана транспортной задачи можно использовать стандартные методы линейного программирования, например, симплекс-метод. Однако ввиду исключительной практической важности этой задачи и специфики ее ограничений [каждая неизвестная входит лишь в два уравнения систем (6.6) и (6.9) и коэффициенты при неизвестных равны единице] для определения оптимального плана транспортной задачи разработаны специальные методы: метод потенциалов, метод дифференциальных рент и др.