Ряд распределения системы двух дискретных величин

			...		...
			...		...
			...		...
...	...	...	...	...	...	...
			...		...
...	...	...	...	...	...	...
			...		...

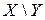
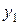
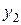
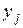
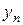
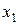
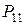
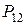
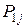
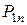
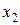
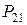
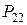
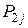
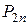
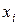
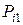
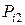
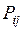
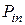
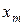
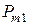
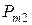
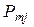
Здесь .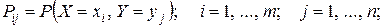

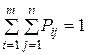2. Функция распределения системы двух случайных величин 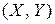- это вероятность совместного выполнения двух неравенств 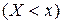и :

.

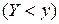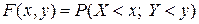Геометрически функция 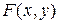есть вероятность попадания случайной точки 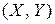в бесконечный квадрант с вершиной в точке 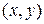, лежащий левее и ниже значения .

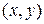Аналогично, как частный случай, функция распределения одной случайной величины 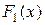есть вероятность попадания случайной точки в полуплоскость, ограниченную справа абсциссой x.

Функция 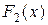есть вероятность попадания точкив полуплоскость, ограниченную сверху ординатой .

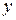Свойства функции :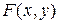

а) 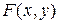есть неубывающая функция обоих своих аргументов, т.е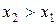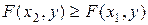. при ; при .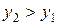

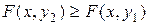б) .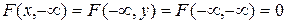

в) 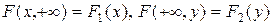, т.е. при одном из аргументов, равном +Ґ, функция распределения системы превращается в функцию распределения одной СВ, соответствующей другому аргументу.

г) .

д) Вероятность попадания случайной точки 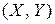в прямоугольник 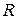, ограниченный абсциссами a и b и ординатами c и d, определяется через 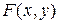по соотношению

.

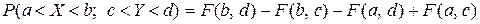3. Плотность распределения системы двух СВ представляет собой предел отношения вероятности попадания в малый прямоугольник к площади этого прямоугольника, когда оба его размера стремятся к нулю. Она может быть выражена как вторая смешанная частная производная функции распределения системы по обоим аргументам:

.

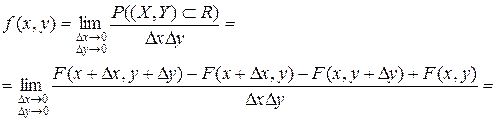
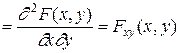Элементом вероятности называется выражение 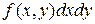. Это вероятность попадания случайной точки 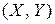в элементарный прямоугольник со сторонами 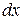, , 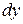примыкающий к точке 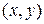. Эта вероятность равна объему элементарного параллелепипеда, ограниченного сверху поверхностью 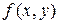и опирающегося на элементарный прямоугольник .

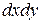Вероятность попадания случайной точки в произвольную область 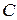может быть получена суммированием (интегрированием) элементов вероятности по всей области :

.

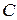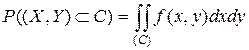Геометрически вероятность попадания в область 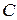изображается объемом цилиндрического тела, ограниченного сверху поверхностью распределения и опирающегося на область 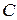. В частности, вероятность попадания случайной точки 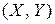в прямоугольник 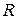, ограниченный абсциссами a и b и ординатами c и d, выражается зависимостью:

.

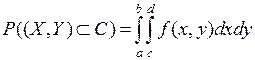Функция распределения 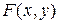выражается через функцию плотности соотношением:

.

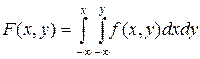Основные свойства плотности распределения системы :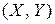

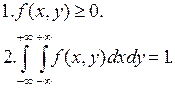
Зная закон распределения системы двух случайных величин, можно всегда определить законы распределения отдельных величин, входящих в систему (маргинальные законы распределения).

Ранее получили: .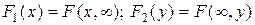

Так как 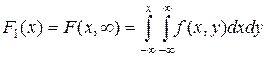, то, дифференцируя последнее выражение по x, будем иметь:

.

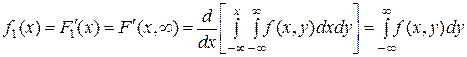Аналогично, .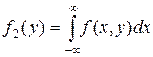

Зная 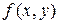, легко определяются 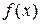и 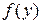. Наоборот - труднее, так как надо знать условные законы распределения.

Условным законом распределения величины X, входящей в систему 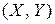, называется ее закон распределения, вычисленный при условии, что другая случайная величина Y приняла определенное значение y. Зная закон распределения одной из величин и условный закон распределения другой, можно составить закон распределения системы.

Теорема умножения законов распределения: .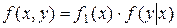

Аналогично: .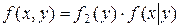

Условные законы распределения можно определить через безусловные:

; .

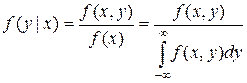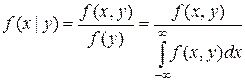Случайная величина 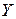называется независимой от случайной величины 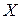, если закон распределения величины 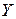не зависит от того, какое значение приняла величина .

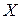Для непрерывных случайных величин условие независимости 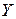от 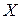может быть записано в виде: 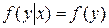при любом у.

Если 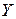зависит от 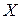, то 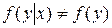. Зависимость или независимость случайных величин всегда взаимны: если величина 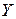не зависит от 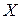, то и величина 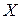не зависит от .

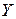Случайные величины 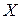и 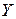называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины 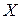и 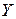называются зависимыми.

Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид: 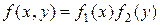, т.е. плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему.

Это условие может рассматриваться как необходимое и достаточное условие независимости случайных величин.