
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числовые характеристики системы двух случайных величин
|
|
Начальным моментом порядка 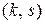 системы
системы 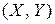 называется математическое ожидание произведения
называется математическое ожидание произведения 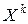 на
на 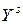 :
: 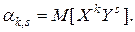
Центральным моментом порядка 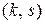 системы
системы 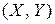 называется математическое ожидание произведения
называется математическое ожидание произведения 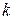 -й и s -й степеней соответствующих центрированных величин:
-й и s -й степеней соответствующих центрированных величин: 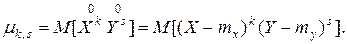
Для дискретных случайных величин начальные и центральные моменты вычисляются, соответственно, по формулам:
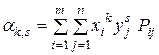 ;
; 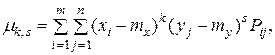
где  - вероятность того, что система
- вероятность того, что система 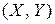 примет значения
примет значения  , а суммирование распространяется по всем возможным значениям случайных величин
, а суммирование распространяется по всем возможным значениям случайных величин 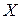 ,
, 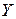 .
.
Для непрерывных случайных величин:
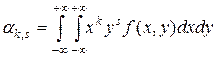 ;
; 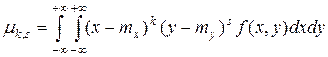 ,
,
где 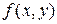 - плотность распределения системы
- плотность распределения системы 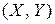 .
.
Очевидно, что 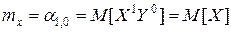 ;
; 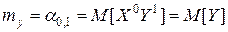 .
.
Совокупность математических ожиданий 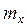 и
и 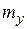 представляет собой характеристику положения центра системы
представляет собой характеристику положения центра системы 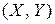 . Геометрически это координаты средней точки на плоскости (центр тяжести), вокруг которой происходит рассеяние всех точек
. Геометрически это координаты средней точки на плоскости (центр тяжести), вокруг которой происходит рассеяние всех точек 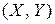 .
.
Дисперсии величин Х и Y характеризуют рассеяние случайной точки в направлении осей 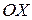 и
и 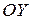 :
:
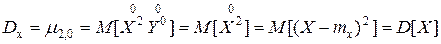 .
.
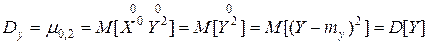 .
.
Особую роль как характеристики системы играет второй смешанный центральный момент 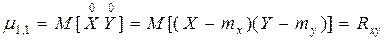 , т.е. математическое ожидание произведения центрированных величин.
, т.е. математическое ожидание произведения центрированных величин.
Это ковариационный момент (т.е. момент связи, корреляционный момент) случайных величин 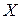 ,
, 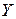 . Для дискретных случайных величин корреляционный момент выражается формулой:
. Для дискретных случайных величин корреляционный момент выражается формулой:
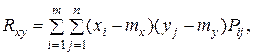
а для непрерывных 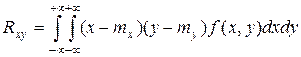 .
.
Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо рассеяния величин 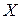 и
и 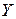 , еще и связь между ними. Для независимых случайных величин корреляционный момент равен нулю.
, еще и связь между ними. Для независимых случайных величин корреляционный момент равен нулю.
Корреляционный момент характеризует не только зависимость величин, но и их рассеяние. Поэтому для характеристики степени тесноты связи между величинами 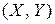 в чистом виде переходят от момента
в чистом виде переходят от момента 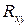 к безразмерной характеристике
к безразмерной характеристике 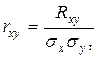 , где
, где 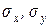 - средние квадратические отклонения величин
- средние квадратические отклонения величин 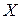 и
и 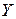 . Эта характеристика называется коэффициентом корреляции величин
. Эта характеристика называется коэффициентом корреляции величин 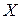 и
и 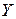 .
.
Две независимые случайные величины всегда являются некоррелированными. Обратное верно не всегда. Равенство нулю коэффициента корреляции (корреляционного момента) есть необходимое, но недостаточное условие независимости случайных величин.
Условие независимости случайных величин - более жесткое, чем условие некоррелированности. Коэффициент корреляции характеризует степень тесноты только линейной зависимости между случайными величинами.
Свойства коэффициента корреляции:
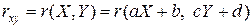 , где
, где 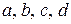 - константы;
- константы; 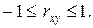
Минимальное число характеристик, с помощью которых может быть охарактеризована система n случайных величин 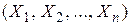 , сводится к следующему: n математических ожиданий
, сводится к следующему: n математических ожиданий 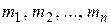 , характеризующих средние значения величин; n дисперсий
, характеризующих средние значения величин; n дисперсий 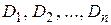 , характеризующих их рассеяние;
, характеризующих их рассеяние; 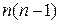 корреляционных моментов
корреляционных моментов 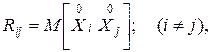
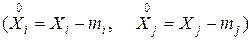 , характеризующих попарную корреляцию всех величин, входящих в систему.
, характеризующих попарную корреляцию всех величин, входящих в систему.
Дисперсия каждой из случайных величин 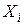 есть частный случай корреляционного момента, а именно, корреляционный момент величины
есть частный случай корреляционного момента, а именно, корреляционный момент величины 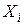 и той же величины
и той же величины 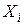 :
: 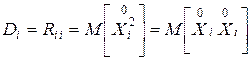 .
.
Все корреляционные моменты и дисперсии удобно располагать в виде симметричной по отношению к главной диагонали квадратной корреляционной матрицы случайных величин 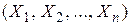 :
:
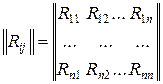 , где
, где 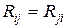 ;
; 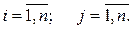
В целях наглядности суждения именно о коррелированности случайных величин безотносительно к их рассеиванию часто пользуются нормированной корреляционной матрицей 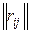 , составленной из коэффициентов корреляции
, составленной из коэффициентов корреляции
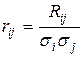 ;
; 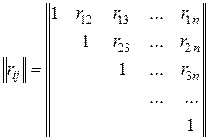 .
.
Плотность нормального распределения двух случайных величин выражается формулой:
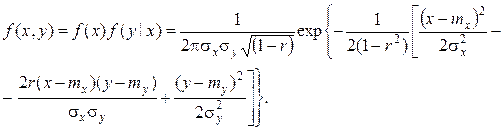
Этот закон зависит от пяти параметров: 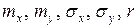 .
.
Параметры 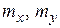 представляют собой математические ожидания (центры рассеивания) величин
представляют собой математические ожидания (центры рассеивания) величин 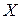 и
и 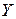 ;
; 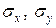 - их средние квадратические отклонения;
- их средние квадратические отклонения; 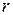 - коэффициент корреляции величин
- коэффициент корреляции величин 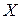 и
и 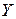 .
.
Если 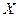 и
и 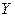 не коррелированы, то
не коррелированы, то
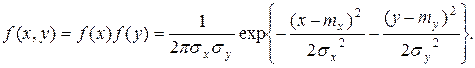
Для системы СВ, подчиненных нормальному закону, из некоррелированности величин вытекает также их независимость.
Термины " некоррелированные" и " независимые" величины для случая нормального распределения эквивалентны.
Условный закон двухмерного нормального распределения:
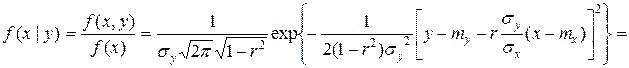
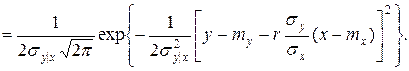
Очевидно, что последнее выражение есть плотность нормального закона с центром рассеяния 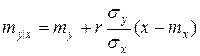 и средним квадратическим отклонением
и средним квадратическим отклонением 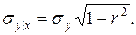
Из последних формул следует, что в условном законе распределения величины 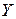 при фиксированном
при фиксированном 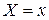 от этого значения зависит только условное математическое ожидание
от этого значения зависит только условное математическое ожидание 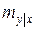 , но не дисперсия.
, но не дисперсия.
Прямая 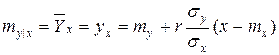 называется линией регрессии
называется линией регрессии 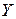 на
на 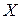 . Аналогично прямая
. Аналогично прямая 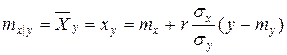 есть линия регрессии
есть линия регрессии 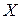 на
на 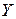 .
.