
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Классификация систем массового обслуживания
|
|
| Классификационные признаки | Разновидности систем массового обслуживания | |||||||||||
| Входящий поток требований | Ограниченность требований | Замкнутые | Открытые | |||||||||
| Закон распределения | Системы с конкретным законом распределения входящего потока: показательным, Эрланга k -го порядка, Пальма, нормальным и т.п. | |||||||||||
| Очередь | Дисциплина очереди | С упорядоченной очередью | С неупорядоченной очередью | С приоритетом обслуживания | ||||||||
| Ограничения ожидания обслуживания | С отказами | С неограниченным ожиданием | С ограничениями (смешанные) | |||||||||
| По длине очереди | По времени ожидания в очереди | По времени пребывания в СМО | Комбинированные | |||||||||
| Дисциплина обслуживания | Этапность обслуживания | Однофазные | Многофазные | |||||||||
| Количество каналов обслуживания | Одноканальные | Многоканальные | ||||||||||
| С равноценными каналами | С неравноценными каналами | |||||||||||
| Надежность каналов обслуживания | С абсолютно надежными каналами | С ненадежными каналами | ||||||||||
| Без восстановления | С восстановлением | |||||||||||
| Взаимопомощь каналов | Без взаимопомощи | С взаимопомощью | ||||||||||
| Достоверность обслуживания | С ошибками | Без ошибок | ||||||||||
| Распределение времени обслуживания | Системы с конкретным законом распределения времени обслуживания: детерминированным, экспоненциальным, нормальным и т.п. | |||||||||||
Если обслуживание производится поэтапно некоторой последовательностью каналов, то такую СМО называют многофазной.
В СМО со «взаимопомощью» между каналами одна и та же заявка может одновременно обслуживаться двумя и более каналами. Например, один и тот же вышедший из строя станок могут обслуживать два рабочих сразу. Такая «взаимопомощь» между каналами может иметь место как в открытых, так и в замкнутых СМО.
В СМО с ошибками заявка, принятая к обслуживанию в системе, обслуживается не с полной вероятностью, а с некоторой вероятностью 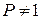 ; другими словами, могут иметь место ошибки в обслуживании, результатом которых является то, что некоторые заявки, пошедшие СМО и якобы «обслуженные», в действительности остаются не обслуженными из-за «брака» в работе СМО.
; другими словами, могут иметь место ошибки в обслуживании, результатом которых является то, что некоторые заявки, пошедшие СМО и якобы «обслуженные», в действительности остаются не обслуженными из-за «брака» в работе СМО.
Примерами таких систем могут быть: справочные бюро, иногда выдающие неправильные справки и указания; корректор, могущий пропустить ошибку или неверно ее исправить; телефонная станция, иногда соединяющая абонента не с тем номером; торгово-посреднические фирмы, не всегда качественно и в срок выполняющие свои обязательства, и т.д.
Для анализа процесса, протекающего в СМО, существенно знать основные параметры системы: число каналов 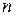 , интенсивность потока заявок
, интенсивность потока заявок 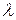 , производительность каждого канала
, производительность каждого канала 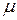 (среднее число заявок, обслуживаемое в единицу времени каналом), условия образования очереди, интенсивность ухода заявок из очереди или системы.
(среднее число заявок, обслуживаемое в единицу времени каналом), условия образования очереди, интенсивность ухода заявок из очереди или системы.
Отношение 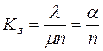 называют коэффициентом загрузки системы. Часто рассматриваются только такие системы, в которых
называют коэффициентом загрузки системы. Часто рассматриваются только такие системы, в которых 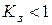 .
.
Время обслуживания в СМО может быть как случайной, так и не случайной величиной. На практике это время чаще всего принимается распределенным по показательному закону 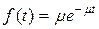
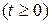 ,
, 
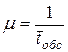 .
.
Основные характеристики СМО сравнительно мало зависят от вида закона распределения времени обслуживания, а зависят главным образом от среднего значения 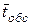 . Поэтому часто пользуются допущением, что время обслуживания распределено по показательному закону.
. Поэтому часто пользуются допущением, что время обслуживания распределено по показательному закону.
Допущения о пуассоновском характере потока заявок и показательном распределении времени обслуживания (которые мы будем предполагать впредь) ценны тем, что позволяют применить в теории массового обслуживания аппарат так называемых марковских случайных процессов.
Эффективность систем обслуживания в зависимости от условий задач и целей исследования можно характеризовать большим числом разных количественных показателей.
Наиболее часто применяются следующие показатели:
1. Вероятность того, что обслуживанием заняты 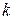 каналов –
каналов – 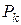 .
.
Частным случаем является 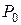 – вероятность того, что все каналы свободны.
– вероятность того, что все каналы свободны.
2. Вероятность отказа заявки в обслуживании 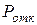 .
.
3. Среднее число занятых каналов 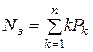 характеризует степень загрузки системы.
характеризует степень загрузки системы.
4. Среднее число каналов, свободных от обслуживания:
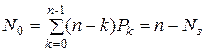 .
.
5. Коэффициент (вероятность) простоя каналов 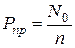 .
.
6. Коэффициент загрузки оборудования (вероятность занятости каналов)
 .
.
7. Относительная пропускная способность 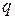 – средняя доля поступивших заявок, обслуживаемая системой, т.е. отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок.
– средняя доля поступивших заявок, обслуживаемая системой, т.е. отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок.
8. Абсолютная пропускная способность 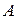 , т.е. число заявок (требований), которое может обслужить система за единицу времени:
, т.е. число заявок (требований), которое может обслужить система за единицу времени:
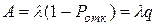 .
.
9. Среднее время простоя канала
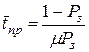 .
.
Для систем с ожиданием используют дополнительно характеристики:
10. Среднее время ожидания требований в очереди 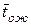 .
.
11. Среднее время пребывания заявки в СМО 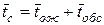 .
.
12. Средняя длина очереди 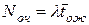 .
.
13. Среднее число заявок в сфере обслуживания (в СМО)
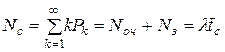 .
.
14. Вероятность того, что время пребывания заявки в очереди не продлится больше определенного времени.
15. Вероятность того, что число требований в очереди, ожидающих начала обслуживания, больше некоторого числа.
Кроме перечисленных критериев при оценке эффективности систем могут быть использованы стоимостные показатели:
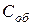 – стоимость обслуживания каждого требования в системе;
– стоимость обслуживания каждого требования в системе;
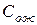 – стоимость потерь, связанных с ожиданием в единицу времени;
– стоимость потерь, связанных с ожиданием в единицу времени;
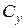 – стоимость убытков, связанных с уходом требований из системы;
– стоимость убытков, связанных с уходом требований из системы;
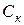 – стоимость эксплуатации канала системы в единицу времени;
– стоимость эксплуатации канала системы в единицу времени;
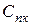 – стоимость единицы простоя канала.
– стоимость единицы простоя канала.
При выборе оптимальных параметров системы по экономическим показателям можно использовать следующую функцию стоимости потерь:
а) для систем с неограниченным ожиданием
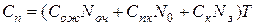 , где
, где 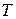 – интервал времени;
– интервал времени;
б) для систем с отказами 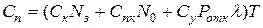 ;
;
в) для смешанных систем 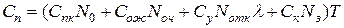 .
.
Варианты, в которых предусматривается строительство (ввод) новых элементов системы (например, каналов обслуживания), обычно сравниваются по приведенным затратам 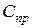 .
.
Приведенные затраты по каждому варианту есть сумма текущих затрат (себестоимости) и капитальных вложений, приведенных к одинаковой размерности в соответствии с нормативом эффективности, например:
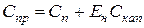 (приведенные затраты за год);
(приведенные затраты за год);
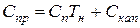 (приведенные затраты за срок окупаемости),
(приведенные затраты за срок окупаемости),
где 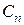 – текущие затраты (себестоимость) по каждому варианту, р.;
– текущие затраты (себестоимость) по каждому варианту, р.;
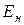 – отраслевой нормативный коэффициент экономической эффективности капитальных вложений (обычно
– отраслевой нормативный коэффициент экономической эффективности капитальных вложений (обычно 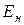 = 0, 15 - 0, 25);
= 0, 15 - 0, 25);
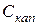 – капитальные вложения по каждому варианту, р.;
– капитальные вложения по каждому варианту, р.;
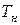 – нормативный срок окупаемости капитальных вложений, лет.
– нормативный срок окупаемости капитальных вложений, лет.
Выражение 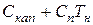 есть сумма текущих и капитальных затрат за определенный период. Их называют приведенными, так как они относятся к фиксированному отрезку времени (в данном случае к нормативному сроку окупаемости).
есть сумма текущих и капитальных затрат за определенный период. Их называют приведенными, так как они относятся к фиксированному отрезку времени (в данном случае к нормативному сроку окупаемости).
Показатели 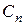 и
и 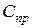 могут применяться как в виде суммы капитальных вложений и себестоимости готовой продукции, так и в виде удельных капитальных вложений на единицу продукции и себестоимости единицы продукции.
могут применяться как в виде суммы капитальных вложений и себестоимости готовой продукции, так и в виде удельных капитальных вложений на единицу продукции и себестоимости единицы продукции.
Для описания случайного процесса, протекающего в системе с дискретными состояниями 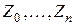 , часто пользуются вероятностями состояний
, часто пользуются вероятностями состояний 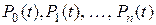 , где
, где 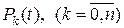 – вероятность того, что в момент
– вероятность того, что в момент  система будет находиться в состоянии
система будет находиться в состоянии 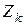 .
.
Очевидно, что 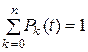 .
.
Если процесс, протекаемый в системе с дискретными состояниями и непрерывным временем, является марковским, то для вероятностей состояний 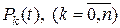 можно составить систему линейных дифференциальных уравнений Колмогорова.
можно составить систему линейных дифференциальных уравнений Колмогорова.
Eсли имеется размеченный граф состояний (рис.4.3) (здесь над каждой стрелкой, ведущей из состояния в состояние, проставлена интенсивность потока событий, переводящего систему из состояния в состояние по данной стрелке), то систему дифференциальных уравнений для вероятностей 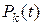 можно сразу написать, пользуясь следующим простым правилом.
можно сразу написать, пользуясь следующим простым правилом.
В левой части каждого уравнения стоит производная 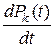 , а в правой части – столько членов, сколько стрелок связано непосредственно с данным состоянием; если стрелка ведет в данное состояние, член имеет знак плюс, если ведет из данного состояния, член имеет знак минус.
, а в правой части – столько членов, сколько стрелок связано непосредственно с данным состоянием; если стрелка ведет в данное состояние, член имеет знак плюс, если ведет из данного состояния, член имеет знак минус.
Каждый член равен плотности потока событий, переводящего систему по данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.
Начальные условия для интегрирования отражают состояние системы в начальный момент. Если, например, система при 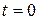 была в состоянии
была в состоянии 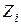 , то полагают
, то полагают
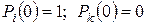
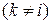 .
.
Предельным режимом для системы 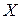 называется случайный процесс, устанавливающийся в системе при
называется случайный процесс, устанавливающийся в системе при 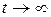 . Если в числе состояний системы имеются состояния без выхода, то при
. Если в числе состояний системы имеются состояния без выхода, то при 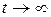 система с практической достоверностью окажется в одном из них.
система с практической достоверностью окажется в одном из них.
Если все потоки событий, переводящие систему из состояния в состояние, стационарны 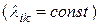 , общее число состояний конечно и состояний без выхода нет, то предельный режим существует и характеризуется предельными вероятностями
, общее число состояний конечно и состояний без выхода нет, то предельный режим существует и характеризуется предельными вероятностями 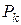
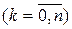 .
.