Прогнозирование спроса на основе марковских процессов

Этот метод аналогичен методу определения спроса на основе анкетных опросов. Рассмотрим это на примере.

Пример 5.2. Пусть имеются три конкурирующих изделия .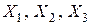

С целью определения спроса на эти изделия произведен опрос 100 человек. Оказалось, что изделие 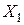покупает 50 человек, изделие - 20 человек, а 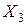- 30 человек.

Предположим, что поведение покупателей в каждый следующий месяц обусловлено только их поведением в предыдущий месяц (таким образом, исследуется простая цепь Маркова).

По истечении месяца оказалось, что из 50 человек, покупавших изделие 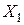, 45 человек продолжают его покупать, 4 человека стали покупать изделие и 1 - изделие 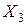. Из 20 человек, покупавших изделие , 6 человек продолжают его покупать, 8 стали покупать изделие 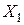, 6 - изделие 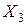. Из 30 человек, покупавших изделие 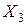, 6 человек продолжают его покупать, 21 человек стал покупать изделие 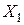, 3 - изделие . Требуется определить, какое изделие пользуется по истечении месяца наибольшим спросом?

Решение. Если 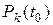- вероятность потребности в изделии 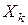в момент 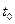, то 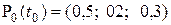. Переходные вероятности определяются из условия задачи: ;

;

.

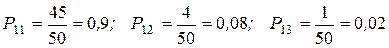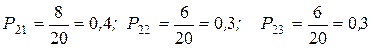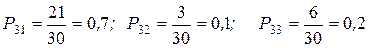Искомые вероятности получаются умножением вектора вероятностей состояния цепи Маркова на переходную матрицу вероятностей. Получаем:

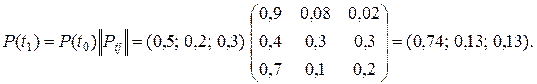
Таким образом, через месяц наибольшим спросом будет пользоваться изделие 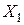. Если предположить, что поведение покупателей со временем не меняется, т.е. что цепь однородна по времени, то аналогично можно определить, какое изделие будет пользоваться наибольшим спросом по истечении двух, трех т.д. месяцев.

Определим, какое изделие будет пользоваться наибольшим спросом по истечении достаточно продолжительного периода.

Все элементы матрицы перехода положительны, следовательно, предельные вероятности 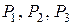потребления изделий 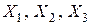существуют.

Система уравнений в данном случае имеет вид

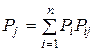, т.е.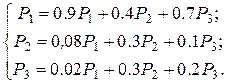

Система линейно зависима. Заменяя третье уравнение системы уравнением 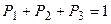, получим систему

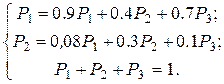
Решение системы: 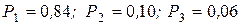.