Решение задачи потребительского выбора и его свойства

Набор 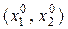, который является решением задачи потребительского выбора, принято называть оптимальным для потребителя, или локальным рыночным равновесием потребителя.

Отметим свойства задачи потребительского выбора.

1. Решение задачи 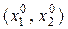сохраняется при любом монотонном преобразовании функции полезности U (x ₁, x ₂). Таким монотонным преобразованием может быть умножение функции полезности на некоторое положительное число, возведение ее в положительную степень, логарифмирование по основанию, большему единицы.

Поскольку значение было максимальным на всем допустимом множестве, оно остается таковым и после монотонного преобразования функции полезности (допустимое множество, определяемое бюджетным ограничением, остается неизменным). Отметим, что свойство 1 должно присутствовать у любой функции полезности; свойства 2 и 3 могут при ее монотонных преобразованиях теряться или приобретаться.

2. Решение задачи потребительского выбора не изменится, если все цены и доход увеличиваются (уменьшаются) в одно и то же число раз l.

Это равнозначно умножению на положительное число l обеих частей бюджетного ограничения 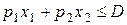, что дает неравенство, эквивалентное исходному. Поскольку ни цены, ни доход D не входят в функцию полезности, задача остается той же, что и первоначально.

В приведенной постановке задача потребительского выбора является задачей нелинейного программирования. Однако, если на каком-то потребительском наборе (x ₁, x ₂) бюджетное ограничение будет выполняться в виде строгого неравенства, то мы можем увеличить потребление какого-либо из продуктов и тем самым увеличить функцию полезности. Следовательно, набор 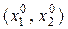, максимизирующий функцию полезности, должен обращать бюджетное ограничение в равенство, т.е. .

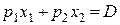Графически это означает, что решение 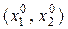задачи потребительского выбора должно лежать на бюджетной прямой, которую удобнее всего провести через точки пересечения с осями координат, где весь доход тратится на один продукт: и .

Будем также считать, что в оптимальной точке 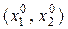условия положительности величин x ₁ и x ₂ выполняются автоматически, вытекая из свойств функции 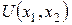. Как правило, это действительно так.

В то же время, если условия неотрицательности переменных не включать в явном виде в условие задачи, то она становится существенно проще с математической точки зрения.

Итак, задачу потребительского выбора можно заменить задачей на условный экстремум, так как решение 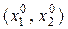этих двух задач одно и то же:

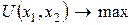при условиях ; .

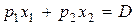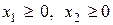Для решения задачи на условный экстремум применим метод Лагранжа.

1) Выписываем функцию Лагранжа

.

2) Находим ее первые частные производные по переменным x ₁, x ₂, l и приравниваем эти частные производные к нулю:

.

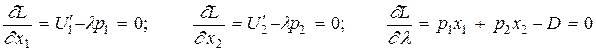Исключив из полученной системы трех уравнений с тремя неизвестными величину l, получим систему двух уравнений с двумя неизвестными :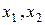

; .

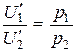Решение 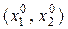этой системы есть решение задачи потребительского выбора (за исключением так называемых угловых решений, которые здесь не рассматриваются).

Подставив решение 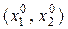в левую часть равенства 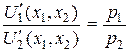получим, что в точке 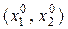локального рыночного равновесия индивидуума отношение предельных полезностей продуктов равно отношению рыночных цен 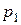, и на эти продукты: .

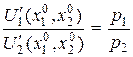В связи с тем, что отношение 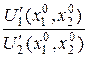равно предельной норме замены первого продукта вторым в точке локального рыночного равновесия 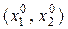, то следует, что эта предельная норма равна отношению рыночных цен 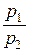на продукты. Приведенный результат играет важную роль в экономической теории.

Геометрически решение 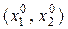можно интерпретировать как точку касания линии безразличия функции полезности 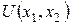с бюджетной прямой 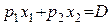. Это определяется тем, что отношение 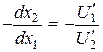показывает тангенс угла наклона линии уровня функции полезности, а отношение – 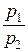представляет тангенс угла наклона бюджетной прямой. Поскольку в точке потребительского выбора (или локального рыночного равновесия) они равны, в этой точке происходит касание данных двух линий. Следовательно 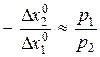, т.е. отношение (со знаком минус) конечных (относительно небольших) изменени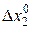й и 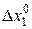объемов продуктов в локальном рыночном равновесии 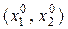приближенно равно отношению рыночных цен p ₁, p ₂ на продукты.

Последнее равенство позволяет давать приближенные оценки отношению рыночных цен, если известны конечные изменения объемов продуктов относительно потребительского набора, приобретенного потребителем, т.е. набора, который естественно следует толковать в качестве оптимального для потребителя.

Координаты решения 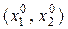задачи потребительского выбора есть функции параметров p ₁, p ₂ и D: , .

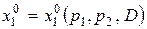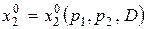Полученные функции называются функциями спроса на первый и второй продукты. Важным свойством функций спроса является их однородность нулевой степени относительно цен и дохода, т.е. значения функций спроса инвариантны по отношению к пропорциональным изменениям цен и дохода (для любого числа ):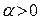

; .

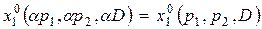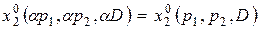Это означает, что если все цены и доход изменятся в одно и то же число раз, величина спроса на продукт (первый или второй - безразлично) останется неизменной.