Общая модель потребительского выбора

Пусть задана целевая функция предпочтения потребителя 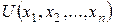(где 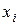- количество 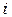-го блага), вектор цен 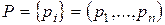и доход 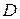. Записав бюджетное ограничение и ограничения на неотрицательность, получаем задачу [9]:

;

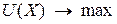при условиях

.

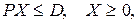
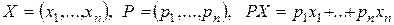Будем, как и ранее, считать, что неотрицательность переменных обеспечивается свойствами целевой функции и бюджетного ограничения. В этом случае можно записать функцию Лагранжа и исследовать ее на безусловный экстремум. Функция Лагранжа будет иметь матричный вид

.

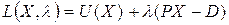Необходимые условия экстремума - равенство нулю частных производных: 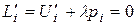для всех i от единицы до n; .

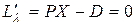Отсюда следует, что для всех i и в точке локального равновесия выполняется равенство 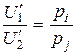. Или в другой форме: .

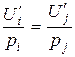Это означает, что дополнительная полезность, приходящаяся на дополнительную единицу денежных затрат, в точке оптимума одинакова по всем видам благ.