
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейные неоднородные уравнения второго порядка
|
|
Рассматриваем линейные неоднородные уравнения (ЛНУ) второго порядка с постоянными коэффициентами
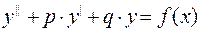 , (6.1)
, (6.1)
где 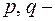 известные числа,
известные числа, 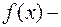 известная функция аргумента
известная функция аргумента  .
.
Общее решение ЛНУ есть сумма общего решение 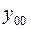 соответствующего ему ЛОУ (5.1) и частного решения
соответствующего ему ЛОУ (5.1) и частного решения 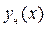 ЛНУ (6.1):
ЛНУ (6.1):
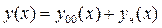 (6.2)
(6.2)
Если правая часть уравнения (6.1) сумма нескольких функций, например, 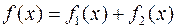 , то его частное решение сумма частных решений ЛНУ с правыми частями
, то его частное решение сумма частных решений ЛНУ с правыми частями 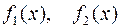 соответственно:
соответственно:
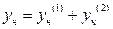 , (6.3)
, (6.3)
где 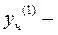 частное решение ЛНУ
частное решение ЛНУ 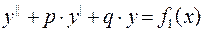 ,
,
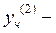 частное решение ЛНУ
частное решение ЛНУ 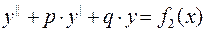 .
.
В инженерной практике распространен метод подбора для правых частей ЛНУ (6.1) специального вида (метод неопределенных коэффициентов)
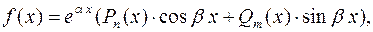 (6.4)
(6.4)
где 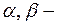 известные числа,
известные числа, 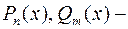 известные многочлены порядков
известные многочлены порядков 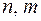 соответственно. Алгоритм подбора вида частного решения приведен в таблице 2. Обозначено:
соответственно. Алгоритм подбора вида частного решения приведен в таблице 2. Обозначено: 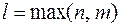 ,
, 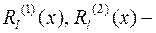 многочлены порядка
многочлены порядка 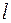 с неопределенными коэффициентами,
с неопределенными коэффициентами, 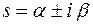 ,
,
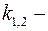 корни характеристического уравнения
корни характеристического уравнения 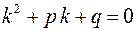 .
.
Таблица 2
Вид функции 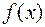
| Вид частного решения |
1. Общий случай
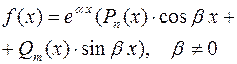
| 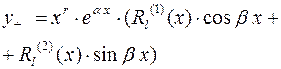 , где , где
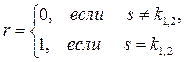
|
2. Частный случай: 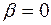 . .
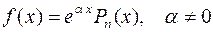 Тогда
Тогда
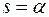
| Тогда 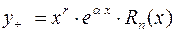
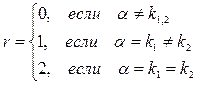
|
3. Частный случай: 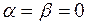
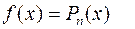 Тогда
Тогда 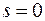 . . 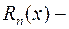 многочлен порядка многочлен порядка 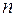 с неизвестными коэффициентами с неизвестными коэффициентами
| 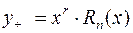 , где , где
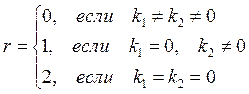
|
Метод неопределенных коэффициентов нельзя применить, если правая часть уравнения (6.1) неспециального вида. Метод Лагранжа (метод вариации произвольных постоянных) можно применить всегда, если найдена ФСР 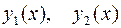 соответствующего однородного уравнения.
соответствующего однородного уравнения.
Согласно методу Лагранжа решение уравнения (6.1) ищется в виде
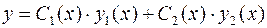 (6.5)
(6.5)
Неизвестные функции 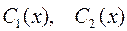 находятся из системы уравнений
находятся из системы уравнений
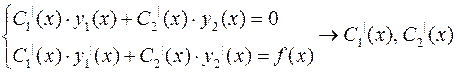 (6.6)
(6.6)
Отсюда
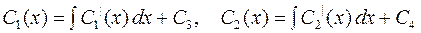 , (6, 7)
, (6, 7)
где 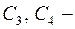 произвольные постоянные.
произвольные постоянные.
Подставив формулы (6.7) в выражение (6.5), получим общее решение линейного неоднородного дифференциального уравнения (ЛНУ) (6.1).
7. Линейные однородные системы с постоянными коэффициентами. Метод Эйлера.
Рассмотрим систему из двух уравнений относительно функций 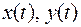
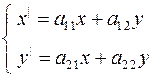 , (7.1)
, (7.1)
где 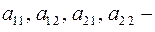 известные числа.
известные числа.
Согласно методу Эйлера решение системы (7.1) ищем в виде
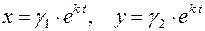
или в матричном виде 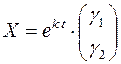 (7.2)
(7.2)
Параметр 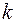 находится из характеристического уравнения [1]
находится из характеристического уравнения [1] 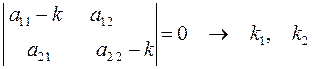 (7.3)
(7.3)
Числа  , соответствующие характеристическому числу
, соответствующие характеристическому числу 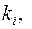
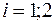 , находятся из системы уравнений
, находятся из системы уравнений
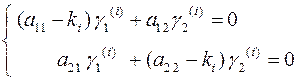 (7.4)
(7.4)
Если корни уравнения (7.3) вещественны и различны (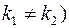 , то общее решение системы (7.1) имеет вид:
, то общее решение системы (7.1) имеет вид:
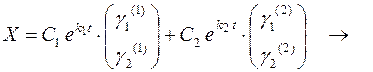
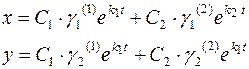 (7.5)
(7.5)
8. Линейные однородные системы с постоянными коэффициентами. Операционный метод.
Полное изложение метода дано в учебнике [1]. В основе метода преобразование Лапласа функции 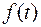
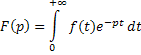 ,
,
где  . Функция
. Функция 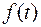 называется оригиналом,
называется оригиналом, 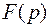 ее изображением. Принято обозначение
ее изображением. Принято обозначение 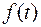 ¸
¸ 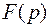 . В таблице 3 приведены изображения основных элементарных функций. Основные теоремы операционного исчисления см. в учебнике [1].
. В таблице 3 приведены изображения основных элементарных функций. Основные теоремы операционного исчисления см. в учебнике [1].
Таблица 3
| № | Оригинал 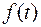
| Изображение 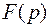
| № | Оригинал 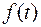
| Изображение 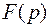
|
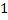
| 
| 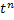
| 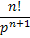
| ||
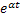
| 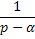
| 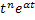
| 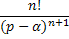
| ||
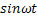
| 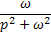
| 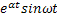
| 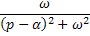
| ||

| 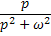
| 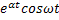
| 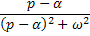
|