Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение с помощью преобразования уравнений.
|
|
Вариант №10.
Условие задачи:
На предприятии имеется сырье видов I, II и III. Из него можно изготовить изделия типов A и B. Запасы сырья на предприятии составляют S1, S2 и S3 единиц соответственно. Изделие типа A дает прибыль c1 у.е., изделие типа B - c2 у.е. Расход сырья на изготовление одного изделия задан в условных единицах таблицей.
| Изделие | Расход сырья на одно изделие | Запасы сырья | Прибыль | |||||
| I | II | III | S1 | S2 | S3 | c1 | c2 | |
| A | ||||||||
| B |
Составить план выпуска изделий, при котором предприятие имеет наибольшую прибыль. Решить задачу симплексным методом:
1. С помощью преобразования уравнений.
2. С помощью симплексных таблиц.
Решение задачи:
Решение с помощью преобразования уравнений.
Целевая функция:
.
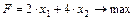Ограничения:
, 
, 
.
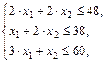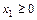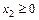С помощью дополнительных неотрицательных переменных перейдем от системы неравенств к системе уравнений:
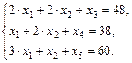
1. Найдем первое базисное решение:
Пусть 
, 
, 
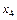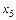- базисные переменные, тогда 
, 
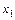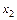- свободные. Выразим базисные переменные через свободные:
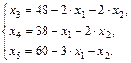
Таким образом, первым базисным решением станет 
при 
, 
.
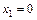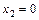Найдем значение целевой функции, выраженной через свободные переменные:
.
.
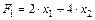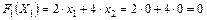Значение функции (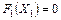
) может возрасти за счет увеличения любой из свободных переменных, входящих в формулу с положительными коэффициентами, следовательно, полученное значение целевой функции не является максимальным, а базисное решение - оптимальным.
2. Перейдем ко второму базисному решению:
Пусть переменная 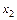станет новой базисной, в связи с тем, что она имеет наибольший положительный коэффициент в целевой функции 
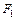. Так как все переменные должны быть неотрицательными, то решим систему неравенств и определим новую свободную переменную:
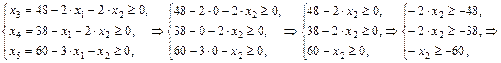
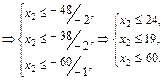
Таким образом, наибольшее возможное значение переменной 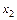, которая станет новой базисной, равно 
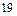и достигается во втором уравнении системы, следовательно, переменная 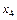станет новой свободной. Уравнение, в котором достигается наибольшее возможное значение переменной, переводимой в базисные, называется разрешающим.
3. Найдем второе базисное решение:
Пусть 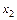, , 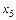- базисные переменные, тогда 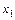, 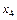- свободные. Выразим новые базисные переменные через новые свободные, начиная с разрешающего уравнения:
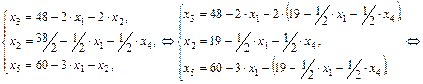
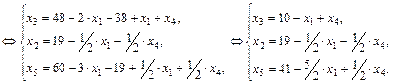
Таким образом, вторым базисным решением станет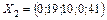 
при ,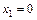 
.
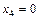Выразим целевую функцию через свободные переменные и найдем ее значение:
.
.
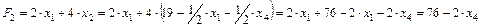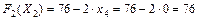Значение функции (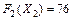
) не может возрасти за счет увеличения свободных переменных, входящих в формулу с отрицательными коэффициентами, следовательно, полученное значение целевой функции является максимальным, а базисное решение - оптимальным.