Решение с помощью симплексных таблиц.

Введем дополнительные неотрицательные переменные в систему уравнений и целевую функцию:

1. Составим первую симплексную таблицу:

Таблица 1.

Базисные переменные		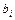Переменные
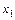
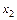
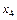
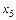
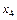
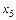
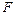
		-2	-4

Критерий оптимальности не выполнен, так как в последней строке присутствуют отрицательные коэффициенты. Наибольший по модулю отрицательный коэффициент в последней строке (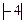) определяет разрешающий столбец ().

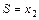Определим оценочные отношения каждой строки первой симплексной таблицы, разделив элементы столбца 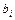на соответствующие элементы разрешающего столбца ():

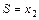Таблица 2.

Базисные переменные		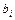Переменные
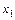
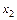
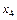
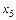
					Оценочное отношение
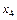
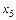
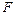
		-2	-4

Минимальное значение оценочного отношения (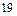) определяет оценочную строку (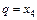). На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент .

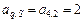2. Перейдем ко второй симплексной таблице по правилам:

- в столбце 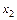запишем новый базис 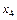(то есть перенесем значения столбца 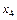в столбец );

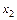- в столбцах, соответствующих базисным переменным, проставим нули и единицы (1 – против «своей» переменной, 0 – против «чужой», 0 – в последней строке базисных переменных);

- новую строку 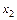получим из старой 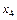путем деления ее значений на разрешающий элемент ;

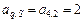- остальные элементы вычислим по правилу прямоугольника.

Таблица 3.

Базисные переменные		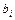Переменные
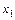
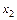
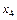
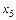
					-1
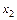
		1/2			1/2
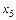
		5/2			-1/2

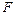
Теперь критерий оптимальности выполнен, так как в последней строке отсутствуют отрицательные коэффициенты, значит 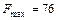при оптимальном базисном решении .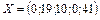