Задача 2. Найти какой-нибудь базис и определить размерность линейного пространства решений системы:

Задача 1.

Найти какой-нибудь базис и определить размерность линейного пространства решений системы:

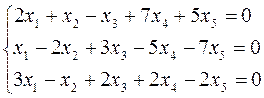
Решение:

Размерность линейного пространства решений этой системы равна рангу матрицы этой системы. Найдём его по методу Гаусса.

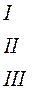
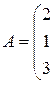
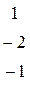
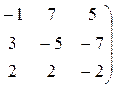
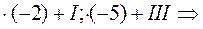
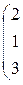
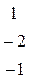
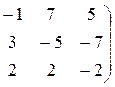
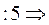
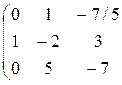
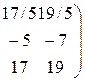
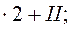
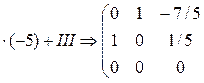
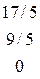
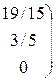
Выделилась единичная матрица 2-го порядка. Ранг матрицы равен порядку выделенной единичной матрицы, т.е. он равен 2. Следовательно, и размерность линейного пространства решений системы равна 2.

Задача 2.

Найти координаты вектора 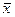в базисе 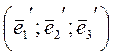, если он задан в базисе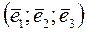

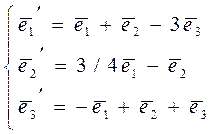
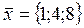
Решение: Запишем вектор 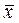в базисе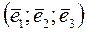

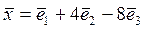
Запишем теперь этот же вектор 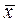в базисе :

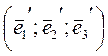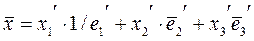, где 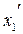; ; 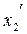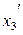- координаты вектора

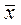в базисе 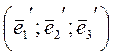, которые и нужно найти.

Приравняем записи вектора 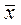в обоих базисах:

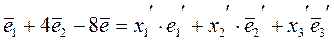
Запишем базисные векторы 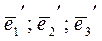через базисные векторы

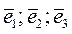(их зависимости даны в системе):

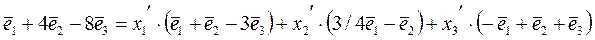
Раскроем скобки:

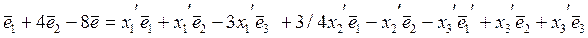
Сгруппируем по базисным векторам:

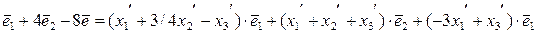
Приравняем коэффициенты перед векторами 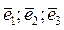соответственно:

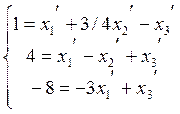
Решим полученную систему по формулам Крамера:

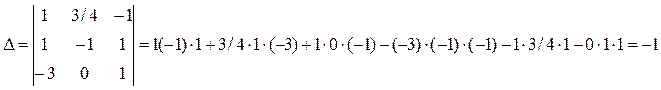
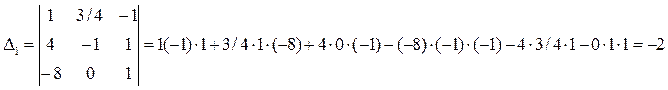
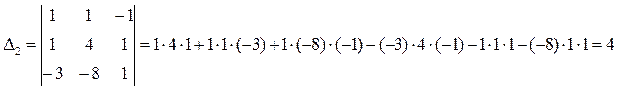
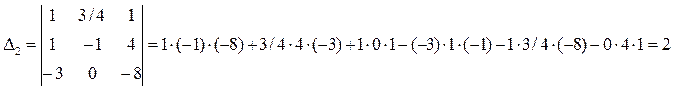
Отсюда:

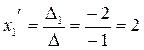
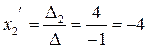
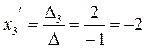
Это координаты вектора 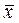в базисе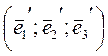

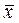={2; -4; -2}

Ответ: 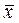={2; -4; -2}

Задача 3: Найти матрицу в базис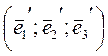е , где ;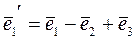

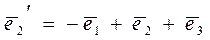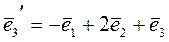; , если она задана в базисе :

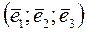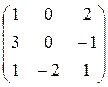
Решение:

Запишем эту матрицу в базисе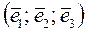

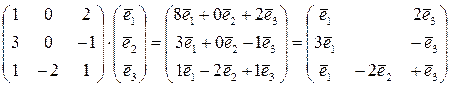
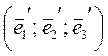
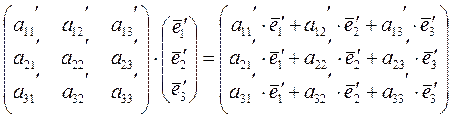Теперь запишем эту же матрицу в базисе

, где

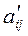- элементы матрицы в базисе

Приравняем полученные записи этой матрицы в разных базисах:

=

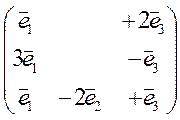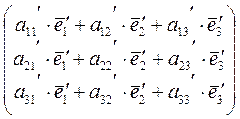
В матрице правой части запишем векторы 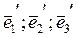через векторы :

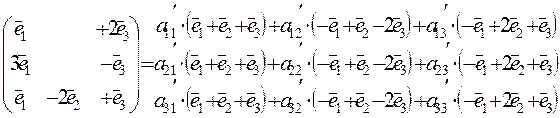
Раскроем скобки:

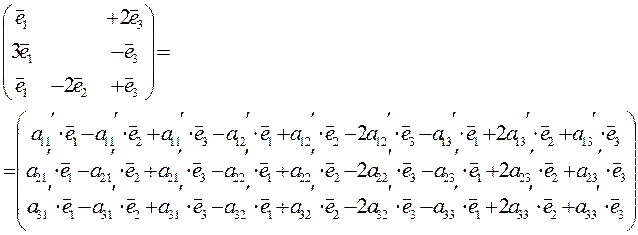
Сгруппируем в матрице правой части по векторам

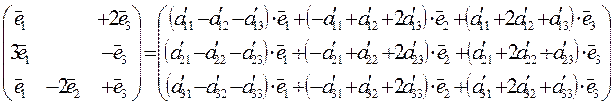
Приравняем коэффициенты перед 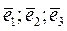соответственно в левой и правой частях, для каждой строки отдельно

Для первой строки:

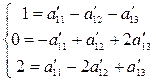
Полученную систему решим по формуле Крамера:

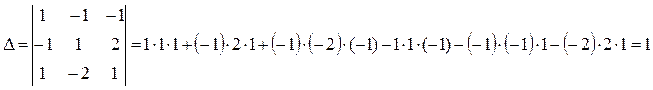
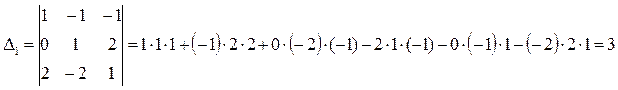
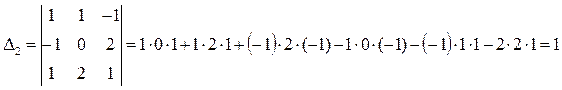
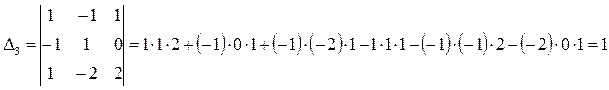
Отсюда:

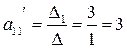
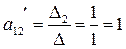
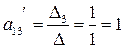
Получили элементы первой строки матрицы в базисе ()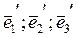

Для второй строки:

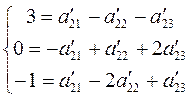
Тоже решим по формуле Крамера:

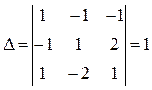
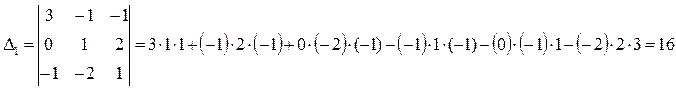
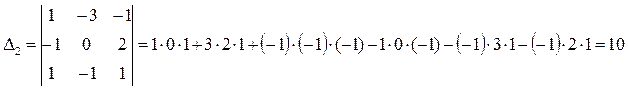
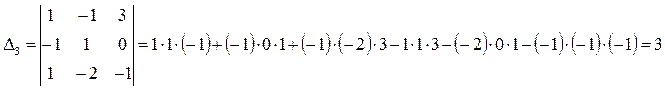
Отсюда:

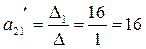
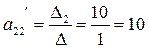
Это элементы второй строки матрицы в базисе ()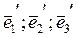

Для третьей строки:

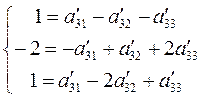
Решим по формуле Крамера:

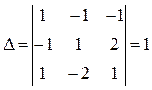
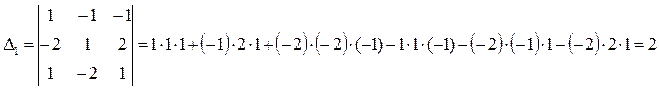
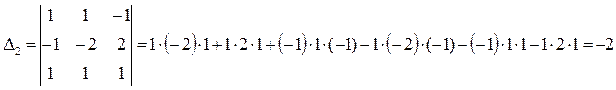
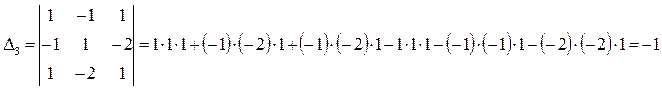Отсюда:

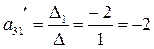
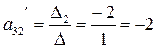
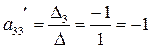
Это элементы третьей строки матрицы в базисе ()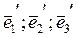

Теперь все найденные элементы запишем в одной матрице:

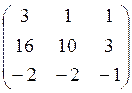
Это матрица в базисе ()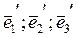

Ответ: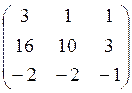

Задача 4. Найти собственные значения и собственные векторы матрицы:

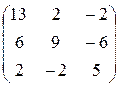
Решение:

Характеристический определитель матрицы:

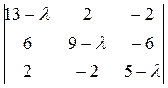
Приравняв его к нулю, получим характеристическое уравнение матрицы:

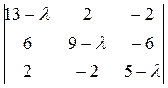=0

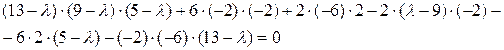
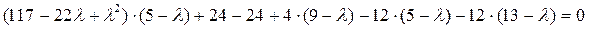
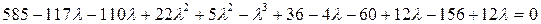
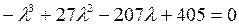
Путём подбора определяем, что один из корней равен 3

Разложим многочлен уравнения на множители:

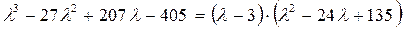
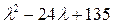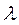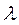Корнями трёхчлена являются =9 и =15

Получаем уравнение:

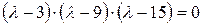
Корни уравнения: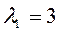

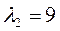
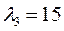
Это собственные значения матрицы. Для каждого собственного значения найдём собственные векторы.

А) для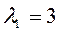

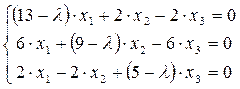
Подставим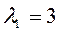

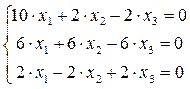или

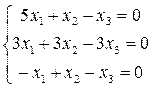
Из первого уравнения вычтем второе: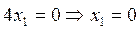

Подставим 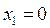во все уравнения системы

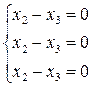
Получим неопределённую систему, в которой =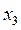

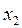
Пусть 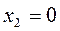, тогда 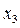= =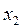0

Собственный вектор: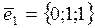

Б) для :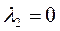

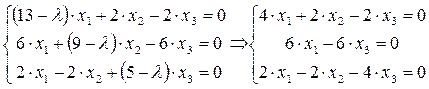
Из второго уравнения: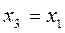

Подставим в первое и третье уравнение

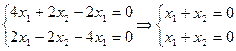
Это неопределённая система. В ней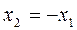

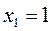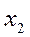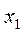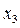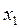Пусть , тогда = - = -1, = =1

Получим второй собственный вектор: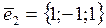

В) для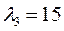

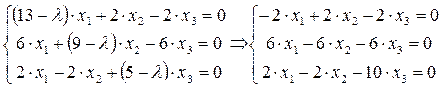
Или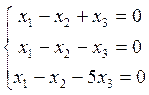

Из первого уравнения вычтем второе: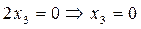

Подставим во все уравнения системы:

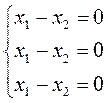
Это неопределённая система, в которой

Пусть , тогда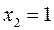

Третий собственный вектор: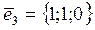

Ответ:

Задача 5. Исследовать кривую второго порядка и построить её.

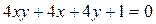
Решение:

Уравнение прямой содержит произведение координат, поэтому для построения графика воспользуемся квадратичной формой.

Квадратичная форма из старших членов:

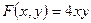
Матрица квадратичной формы: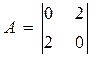

Характеристическое уравнение этой матрицы:

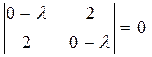или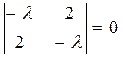

Раскрыв определитель, получим

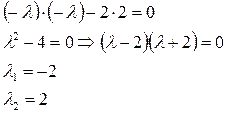
В новой системе координат квадратичная форма записывается

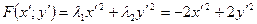
Теперь нужно найти младшие члены уравнения этой кривой в новой системе координат:

Матрица преобразования: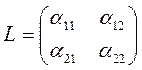

Для 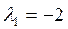запишем систему:

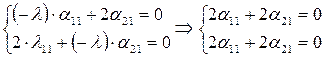
Это неопределённая система, потому что уравнения системы одинаковы. В этой системе 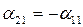. Запишем для матрицы преобразования:

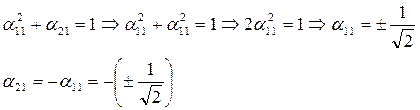
Для 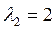запишем систему:

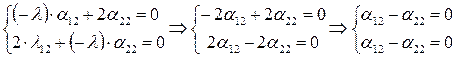
Снова получим неопределённую систему, в которой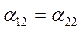

Для матрицы преобразования:

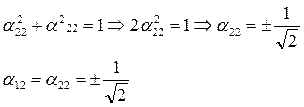
Для определённости возьмём один знак:

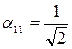
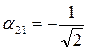
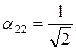
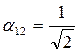
Матрица преобразования:

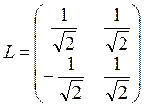
По формулам преобразования координат запишем:

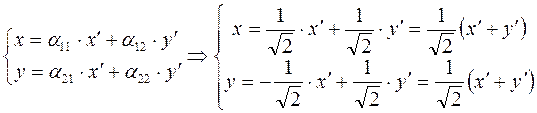
Запишем младшие члены уравнения кривой и подставим новые координаты:

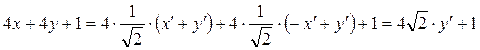
Подставим в уравнение кривой старшие и младшие члены в новых координатах:

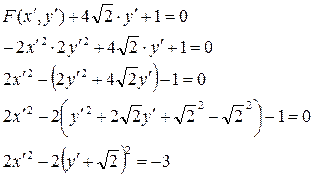
Поделим на -3 обе части уравнения:

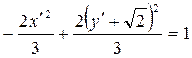
Получим каноническое уравнение гиперболы в системе координат

, центр которой смещён 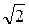на вниз по оси, и у которой действительная и мнимая полуоси равны .

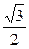При построении ос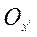и и 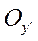повернуты относительно осе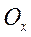й и 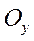на угол 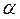, для которого: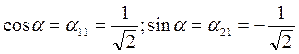

, отсюда: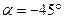

Оси поворачиваются на 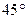относительно точки 0(0; 0) по часовой стрелке.

Действительная полуось гиперболы – по оси 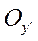, а мнимая – по оси 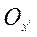, так как перед координатой стоит знак «+», а перед координатой - знак «-«.

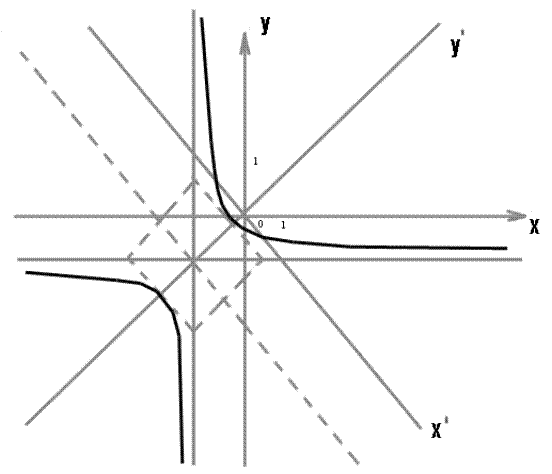
Построим кривую в новой системе координат:

Построение:

А) в системе координат 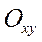построим систему координат , повернув оси на 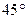по часовой стрелке вокруг точки 0(0, 0).

Б) Сместим центр гиперболы на 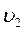вниз по оси 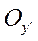(проведена штриховая линия параллельно оси)

В)Проведём штриховые линии параллельно проведённой штриховой линии на расстоянии 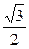с каждой стороны, и также проведём штриховые линии параллельно оси на расстоянии 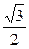с двух сторон. Через их точки пересечения проведём асимптоты.

Г) Построим график найденной гиперболы в системе