Сенімділік көрсеткіштерінің статистикалық қатарын құрастыру

Сынақ қ а тү скен қ озғ алтқ ыштардың саны немесе алғ ашқ ы ақ параттар саны N-таң басымен белгіленеді..

Егер, N< 25 болса, онда ақ параттың статистикалық қ атары кестесін қ ұ рмайды. Қ арастырып отырғ ан мысалда бақ ылаудағ ы қ озғ алтқ ыштар саны N=70> 25(кесте 1) болғ андық тан, ақ параттардың статистикалық қ атарының кестесі қ ұ рылады.

Ақ параттардың статистикалық қ атары кестесін қ ұ ру ү шін берілген ақ параттық кө рсеткіштерді(N) біркелкі «n» интервалғ а бө леді. Келесі интервалдың мә ні оның алдындағ ы интервалдың мә німен жалғ асып жатуы тиіс. Интервалдың жалпы саны кө бейген сайын есептеудің дә лдігі де арта береді.

Статистикалық қ атардағ ы интервалдар санын мына формуламен анық тайды

n = √ N+1

Мұ ндағ ы алғ ашқ ы берілген ақ параттар саны N=66.

Интервалдар санын анық таймыз

n =√ 70 + 1=8, 36 + 1= 9, 36 = 9

Есептеулер нә тижесін тұ тас санғ а дейін келтіріп қ абылдаймыз.Сондық тан n=9.

Интервал қ ашық тығ ы А-деп белгіленеді.

Оның мә нін мына формуламен анық таймыз

А = (t_max – t_min)/n

мұ нда t_max, t_min – сенімділік кө рсеткіштерінің немесе қ озғ алтқ ыш ресурсының максимальды жә не минимальді мә ндері

А = (62000 – 10000)/9=5777, 777

Кө рсеткіштің аталуы	Интервал бойынша кө рсеткіштердің мә ні
Интервал, tі, мың.мото-с	10- 15, 77	15, 77- 21, 55	21, 55- 27, 33	27, 33- 33, 11	33, 11- 38, 88	38, 88- 44, 66	44, 66- 50, 44	50, 44- 56, 22	56, 22- 62, 0
Интервал ортасы, tci	12, 88	18, 66	24, 44	30, 22	36, 00	41, 7	47, 55	55, 33	59, 11
Тә жірибелік жиілік, mi
Тә жірибелік ық тималдылық, рі	0, 11	0, 1	0, 17	0, 14	0, 24	0, 15	0, 05		0, 01
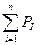
Тә жірибелік ық тималдылық жиынтығ ы,	0, 11	0, 21	0, 38	0, 66	0, 91	1, 06	1, 12	1, 12	1, 13

Кестенің «Интервал» жолында сенімділік кө рсеткішінің ө лшем бірлігіндегі ә рбір интервалдың шекарасын, одан кейінгі жолдарда тә жірибелік жиілікті -m_i немесе ә рбір интервалдағ ы қ арсылық тар санын, тә жірибелік ық тималдылық ты т.с.с. кө рсетеді.

Егер ақ парат нү ктесі тура шекарағ а тү сетін болса, онда ол нү ктенің мә ні шекаралас интервалдарғ а 0, 5- тен беріледі.

Тә жірибелік ық тималдылық мына формуламен анық талады р_і = m_i / N

мұ нда m_i – статистикалық қ атардың і-интервалындағ ы тә жірибелік жиілік немесе интервалдағ ы қ арсылық саны;

N – сынауғ а жіберілген жалпы қ озғ алтқ ыштар(машиналар, объектілер) саны.

Формула бойынша бірінші интервалдағ ы тә жірибелік ық тималдылық р_і=9/70=0, 12 мә ніне тең, екінші интервалдағ ы тә жірибелік ық тималдылық р_і=0, 13тең. Интервалдардағ ы тә жірибелік ық тималдылық тар мә ні кестеде келтірілген.

Тә жірибелік ық тималдылық тар жиынтығ ы статистикалық қ атардағ ы интервалдардың тә жірибелік ық тималдылық тарының қ осындысымен анық талады. Бірінші интервалдағ ы жиынтық тә жірибелік ық тималдылық сол интервалдың тә жірибелік ық тималдылығ ына тең болады. Екінші интервалдағ ы жиынтық тә жірибелік ық тималдылық бірінші жә не екінші интервалдардың тә жірибелік ық тималдылық тарының қ осындысына тең:

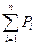. = 0, 12 + 0, 12 = 0, 24

Ү шінші интервалдағ ы жиынтық тә жірибелік ық тималдылық бірінші, екінші жә не ү шінші интервалдардың тә жірибелік ық тималдылық тарының қ осындысына тең.

Статистикалық қ атардың жиынтық тә жірибелік ық тималдылық тары 3-кестеде келтірілген.

Сонымен қ атар, статистикалық қ атардың жиынтық тә жірибелік ық тималдылық тарының қ осындысы бірге тең болады.