I-й учебный вопрос

Классификация СеМО - 35 мин

В зависимости от структуры и свойств исследуемых систем их моделями могут служить СеМО различных классов. Одна из возможных классификаций сетевых моделей приведена на рис.3.6.

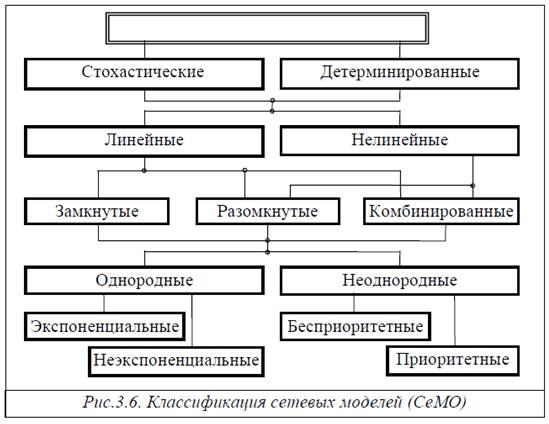
1. В зависимости от характера процессов поступления и обслуживания заявок в сети СеМО делятся на:

- стохастические, в которых процессы поступления и/или обслуживания заявок носят случайный характер, то есть интервалы времени между поступающими заявками и/или длительности их обслуживания в узлах представляют собой случайные величины, описываемые соответствующими законами распределений;

- детерминированные, в которых интервалы времени между поступающими заявками и длительности их обслуживания в узлах являются детерминированными величинами.

2. По виду зависимостей, связывающих интенсивности потоков заявок в разных узлах, СеМО делятся на:

- линейные, если эти зависимости линейные;

- нелинейные, если эти зависимости являются нелинейными.

В линейных СеМО, как это следует из определения, интенсивность потока заявок в узел j связана с интенсивностью потока заявок в узел i линейной зависимостью:

λ j =α ij* λ i,

где α ij – коэффициент пропорциональности, показывающий, во сколько раз отличаются интенсивности потоков заявок в узел j и в узел i (i, j = 1, ¯ n).

Поскольку указанная зависимость справедлива для любой пары узлов, это выражение можно записать в несколько ином виде и выразить интенсивность поступления заявок во все узлы j = 1, ¯ n через одну и ту же интенсивность, например, через интенсивность λ 0 потока заявок, поступающих в СеМО из источника заявок:

Λ j=α j*λ 0. (3.5)

В последнем выражении коэффициент пропорциональности α j≥ 0 показывает, во сколько раз интенсивность потока заявок в узел j (i, j = 1, ¯ n) отличается от интенсивности источника заявок, и называется коэффициентом передачи. Коэффициент передачи может принимать любое положительное значение.

Коэффициент передачи играет важную роль при разработке математических зависимостей и расчете характеристик функционирования сетевых моделей. Это обусловлено тем физическим смыслом, который несет в себе коэффициент передачи.

Коэффициент передачи можно трактовать как среднее число попаданий заявки в данный узел за время ее нахождения в сети. Например, если коэффициент передачи узла СеМО равен 3, то это означает, что любая заявка за время нахождения в сети в среднем 3 раза побывает на обслуживании в данном узле. Значение коэффициента передачи, равное 0, 25, будет означать, что в среднем только одна заявка из четырёх попадёт на обслуживание в данный узел, а три другие обойдут данный узел стороной.

В нелинейных СеМО интенсивности потоков заявок в узлах связаны более сложными нелинейными зависимостями, что значительно усложняет их исследование.

Нелинейность СеМО может быть обусловлена:

· потерей заявок в сети, например из-за ограниченной емкости накопителей в узлах;

· размножением заявок в сети, заключающимся, например, в формировании нескольких новых заявок после завершения обслуживания некоторой заявки в одном из узлов сети.

Таким образом, СеМО является линейной, если в ней заявки не размножаются и не теряются. Ниже рассматриваются, в основном, линейные СеМО.

3. По числу циркулирующих в сети заявок различают СеМО:

- разомкнутые;

- замкнутые;

- замкнуто-разомкнутые.

4. По типу циркулирующих заявок различают СеМО:

□ однородные, в которых циркулирует один класс заявок (однородный поток заявок);

□ неоднородные, в которых циркулирует несколько классов заявок (неоднородный поток заявок), различающихся хотя бы одним из следующих факторов:

· длительностями обслуживания в узлах;

· приоритетами;

· маршрутами.

Маршруты заявок разных классов задаются путем указания номеров классов заявок на соответствующих дугах сети (рис.3.7, г).

ВЫВОД

В зависимости от структуры и свойств исследуемых систем их моделями могут служить СеМО различных классов. Сетевые модели классифицируются следующим образом: