
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры выполнения задач типового расчета
|
|
Задача 1. Стрелок стреляет в мишень до первого попадания, но не более четырех раз. Вероятность попадания при одном выстреле равна р = 0, 6. Дискретная случайная величина Х – число затраченных патронов. Найти распределение вероятностей величины Х, вычислить М (Х), D (X), σ (Х). Определить вероятность Р того, что стрелок израсходует не менее трех патронов. Найти функцию распределения F (x) и построить ее график.
Решение: Все расчеты приведены в таблице 1.3. Случайная величина Х принимает значения Х = n (n = 1, 2, 3, 4). Подсчитаем их вероятности. Пусть вероятность промаха q = 1 – p = 0, 4. Очевидно, Р (Х = 1) = р (стрелок попал с первого раза), Р (Х = 2) = qp (стрелок первый раз промахнулся, а во второй раз попал), Р (Х = 3) = q 2 p (стрелок два раза промахнулся, а в третий раз попал), Р (Х = 4) = q 3 p + q 4 (стрелок три раза промахнулся, а в четвертый раз попал; или четыре раза промахнулся, но и в этом случае Х = 4, так как стрелок стреляет не более четырех раз).
| Таблица 1.3 | ||||
| X | P | X·P | X 2· P | F (x) |
| 0, 6 | 0, 6 | 0, 6 | ||
| 0, 4 · 0, 6 = 0, 24 | 0, 48 | 0, 96 | 0, 6 | |
| 0, 42 · 0, 6 = 0, 096 | 0, 288 | 0, 864 | 0, 84 | |
| 0, 43 · 0, 6 + 0, 44 = 0, 064 | 0, 256 | 1, 024 | 0, 936 | |
| ∑ | 1, 000 | 1, 624 | 3, 448 |
Расчет математического ожидания случайных величин X и X 2 также приведен в таблице 1.3 по формулам (1.18), (1.22):
M (X) = 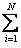 xi pi; M (X 2) =
xi pi; M (X 2) = 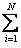 xi 2 pi; D (X) = M (X 2) – (M (X))2.
xi 2 pi; D (X) = M (X 2) – (M (X))2.
В столбцах XP и X 2 P записаны значения произведений xi pi и xi 2 pi. В последней строке – суммы элементов соответствующих столбцов.
M (X) = 1, 624; M (X 2) = 3, 448; D (X) = 3, 448 – 1, 624 2 ≈ 0, 81; σ ≈ 0, 9.
Вероятность того, что стрелок израсходует не менее трех патронов соответствует вероятности события X ≥ 3:
P(X ≥ 3) = P (X = 3) + P (X = 4) = 0, 096 + 0, 064 = 0, 16.
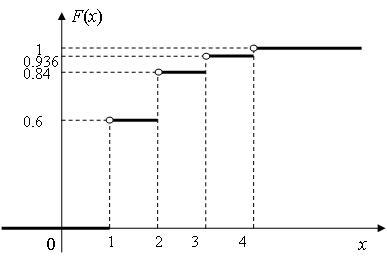
Риснок 1.2
Функцию распределения F (х) находим по формуле (1.15) как функцию накопленных вероятностей 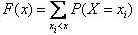 , где суммирование распространяется на все значения индекса i, для которых xi < x. Полученные значения функции распределения записаны в последнем столбце таблицы 1.3.
, где суммирование распространяется на все значения индекса i, для которых xi < x. Полученные значения функции распределения записаны в последнем столбце таблицы 1.3.
Искомая функция распределения имеет вид: 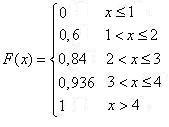
График функции распределения представлен на рис. 1.2.
Ответ: M (X) = 1, 624; D (X) ≈ 0, 81; σ ≈ 0, 9; P (X) = 0, 16.
Задача 2. Стрелок делает пять независимых выстрелов в мишень. вероятность попадания в цель при одном выстреле равна 0, 6. Случайная величина Х – число попаданий в цель. Найти распределение вероятностей величины Х, вычислить М (Х), D (X), σ (Х). Определить вероятность Р того, что цель будет поражена, т.е. будет хотя бы одно попадание. Найти функцию распределения F (x) и построить ее график.
Решение: Дискретная случайная величина Х имеет биномиальное распределение, где n = 5, р = 0, 6, q = 0, 4, тогда вероятности P (X = m) можно вычислить по формуле (1.16):
P (X = 0) = P 5(0) = C 50 p 0 q 5 = (0, 4)5 = 0, 0102.
P (X = 1) = P 5(1) = C 51 p 1 q 4 = 5 · 0, 6 · (0, 4)4 = 0, 0768.
P (X = 2) = P 5(2) = C 52 p 2 q 3 = 10 · 0, 62 · (0, 4)3 = 0, 2304.
P (X = 3) = P 5(3) = C 53 p 3 q 2 = 10 · 0, 63 · (0, 4)2 = 0, 3456.
P (X = 4) = P 5(4) = C 54 p 4 q 1 = 5 · 0, 64 · (0, 4) = 0, 2592.
P (X = 5) = P 5(5) = C 55 p 5 q 0 = 0, 65 = 0, 0778.
Проверка: 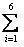 pi = 0, 0102 + 0, 0768 + 0, 2304 + 0, 3456 + 0, 2592 + 0, 0778 = 1.
pi = 0, 0102 + 0, 0768 + 0, 2304 + 0, 3456 + 0, 2592 + 0, 0778 = 1.
Распределение вероятностей случайной величины Х приведено в табл. 1.4.
Математическое ожидание и дисперсия дискретной случайной величины Х, имеющей биномиальное распределение, могут быть найдены по формулам (1.23):
M (X) = np = 5 · 0, 6 = 3; D (X) = npq = (np) q = 3 · 0, 4 = 1.2; σ (X) = 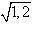 ≈ 1, 095.
≈ 1, 095.
| Таблица 1.4 | ||
| X | P | F (x) |
| (0, 4)5 = 0, 0102 | ||
| 5 · 0, 6 · (0, 4)4 = 0, 0768 | 0, 0102 | |
| 10 · (0, 6)2 · (0, 4)3 = 0, 2304 | 0, 087 | |
| 10 · (0, 6)3 · (0, 4)2 = 0, 3456 | 0, 3174 | |
| 5 · (0, 6)4 · 0, 4 = 0, 2592 | 0, 663 | |
| (0, 6)5 = 0, 0778 | 0, 9222 | |
| ∑ | 1, 000 |
Вероятность того, что цель будет поражена, т.е. будет хотя бы одно попадание соответствует вероятности события X ≥ 1.
P (X ≥ 1) = 1 – P (X = 0) = 1 – 0, 0102 = 0, 9898.
Функцию распределения F (х) находим по формуле (1.15) как функцию накопленных вероятностей 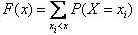 , где суммирование распространяется на все значения индекса i, для которых xi < X. Полученные значения функции распределения записаны в последнем столбце таблицы 1.4.
, где суммирование распространяется на все значения индекса i, для которых xi < X. Полученные значения функции распределения записаны в последнем столбце таблицы 1.4.
Искомая функция распределения имеет вид: 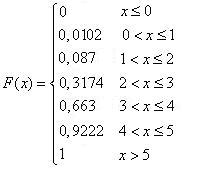 .
.
График функции распределения представлен на рис. 1.3.
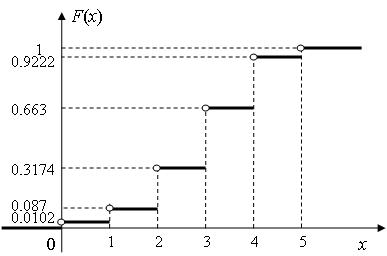
Рисунок 1.3
Ответ: M (X) = 3; D(X) = 1, 2; σ ≈ 1, 095; Р = 0, 9898.
Задача 3. В партии из 30 деталей имеется 8 нестандартных, остальные стандартные. Наудачу отобраны 6 деталей. Х – числа стандартных деталей среди отобранных. Найти распределение вероятностей дискретной случайной величины Х, вычислить М (Х), D (X), σ (Х). Определить вероятность Р того, что среди отобранных деталей не более двух нестандартных. Найти функцию распределения F (x) и построить ее график.
Решение: P (X = 0) = Р (все 6 деталей нестандартные) =
=(8/30)(7/29)(6/28)(5/27)(4/26)(3/25) ≈ 0, 00005.
P (X = 1) = Р (одна деталь стандартная, остальные нестандартные) =
= 6 · (22/30)(8/29)(7/28)(6/27)(5/26)(4/25) ≈ 0, 00207.
Найдена вероятность события: первая вынутая деталь стандартная, остальные нестандартные. Но стандартная деталь может быть вынута первой, второй, третьей, …, шестой, т.е. возможно шесть несовместных событий (вариантов), а искомое событие X = 1 является их суммой. Вероятность каждого варианта одинакова, поэтому найденная вероятность умножена на 6.
P (X = 2) = Р (две детали стандартные, остальные нестандартные) =
= C 62 · (22/30) (21/29) (8/28) (7/27) (6/26) (5/25) ≈ 0, 02723.
Найдена вероятность события: две первые вынутые детали стандартные, остальные нестандартные. Эта вероятность умножена на число вариантов, которыми можно вынуть две детали из шести, т.е. на 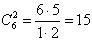 .
.
P (X = 3) = Р (три детали стандартные, остальные нестандартные) =
= C 63 · (22/30) (21/29) (20/28) (8/27) (7/26) (6/25) ≈ 0, 1452.
Найдена вероятность события: три первые вынутые детали стандартные, остальные нестандартные. Эта вероятность умножена на число вариантов, которыми можно вынуть три детали из шести, т.е. на 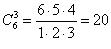 .
.
P (X = 4) = Р (четыре детали стандартные, остальные нестандартные) =
= C 64 · (22/30) (21/29) (20/28) (19/27) (8/26) (7/25) ≈ 0, 3449.
P (X = 5) = Р (пять деталей стандартные, остальные нестандартные) =
= C 65 ·(22/30) (21/29) (20/28) (19/27) (18/26) (8/25) ≈ 0, 3548.
P (X = 6) = Р (все шесть деталей стандартные) =
= (22/30) (21/29) (20/28) (19/27) (18/26) (17/25) ≈ 0, 1257.
Распределение вероятностей случайной величины X приведено табл. 1.5. Вероятность события X = 0 получилась равной нулю, так как расчет вероятностей проводился с точностью четыре знака после запятой. При более точном расчете P (X = 0) = 0, 000047.
| Таблица 1.5 | ||||
| X | P | XP | X 2 P | F (x) |
| (8/30)(7/29)(6/28)(5/27)(4/26)(3/25) ≈ 0, 0000 | 0, 0000 | 0, 0000 | ||
| 6 · (22/30)(8/29)(7/28)(6/27)(5/26)(4/25) ≈ 0, 0021 | 0, 0021 | 0, 0021 | ||
| 15 · (22/30)(21/29)(8/28)(7/27)(6/26)(5/25) ≈ 0, 0272 | 0, 0544 | 0, 1088 | 0, 0021 | |
| 20 · (22/30)(21/29)(20/28)(8/27)(7/26)(6/25) ≈ 0, 1452 | 0, 4356 | 1, 3068 | 0, 0293 | |
| 15 · (22/30)(21/29)(20/28)(19/27)(8/26)(7/25) ≈ 0, 3450 | 1, 3800 | 5, 5200 | 0, 1745 | |
| 6 · (22/30)(21/29)(20/28)(19/27)(18/26)(8/25) ≈ 0, 3548 | 1, 7740 | 8, 8700 | 0, 5195 | |
| (22/30)(21/29)(20/28)(19/27)(18/26)(17/25) ≈ 0, 1257 | 0, 7542 | 4, 5252 | 0, 8743 | |
| ∑ | 1, 000 | 4, 4003 | 20, 3329 |
Расчет математического ожидания случайных величин X и X 2 также приведен в таблице 1.5 по формулам (1.18), (1.22). В столбцах XP и X 2 P записаны значения произведений xi pi и xi 2 pi. В последней строке – суммы элементов соответствующих столбцов.
M (X) ≈ 4, 4; M (X 2) = 20, 3329; D (X) = 20, 3329 – 4, 40032 ≈ 0, 97; σ ≈ 0, 985.
Вероятность того, что среди отобранных деталей не более двух нестандартных соответствует вероятности события X ≥ 4.
P (X ≥ 4) = P (X = 4) + P (X = 5) + P (X = 6) = 0, 3450+0, 3548+0, 1257 = 0, 8255.
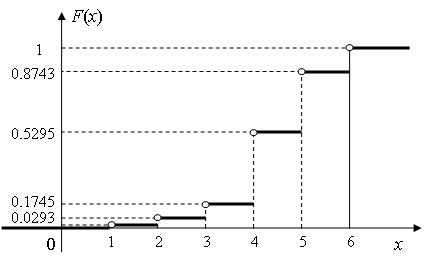
Рисунок 1.4
Функцию распределения F (х) находим по формуле (1.15) как функцию накопленных вероятностей 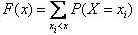 , где суммирование распространяется на все значения индекса i, для которых xi < x. Полученные значения функции распределения записаны в последнем столбце таблицы 1.5.
, где суммирование распространяется на все значения индекса i, для которых xi < x. Полученные значения функции распределения записаны в последнем столбце таблицы 1.5.
Искомая функция распределения имеет вид: 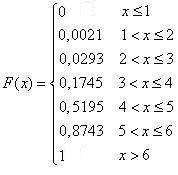 .
.
График функции распределения представлен на рис. 1.4.
Ответ: M (X) = 4.4; D (X) = 0, 97; σ ≈ 0, 985; Р = 0, 8255.