Двумерный случайный вектор. Линейная корреляция

Обработка данных методами линейного корреляционного анализа

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Двумерный случайный вектор. Линейная корреляция

Рассмотрим систему двух случайных величин или двумерный случайный вектор (X, Y) ^T c центром распределения 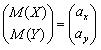и ковариационной матрицей

,

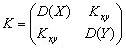(5.1)

где a_x и a_y – математические ожидания; D (X) = σ _x ² и D (Y) = σ _y ² – дисперсии случайных величин X и Y соответственно; K_xy – ковариация между величинами X и Y, определяется следующим образом:

В качестве нормированной ковариации вводится коэффициент корреляции:

,

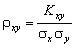(5.3)

который характеризует степень линейной зависимости между случайными величинами X и Y.

Свойства коэффициента корреляции следующие.
1. Коэффициент корреляции является безразмерным коэффициентом, не зависящим от начала отсчета величин X и Y.
2. Коэффициент корреляции по абсолютной величине не превышает единицу: –1 ≤ ρ _xy ≤ 1.
3. Если |ρ _xy | = 1, случайные величины X и Y связаны линейной функциональной зависимостью.
4. Если ρ _xy = 0, случайные величины X и Y некоррелированы, т.е. между ними отсутствует линейная зависимость.
5. Чем ближе значение |ρ _xy | к единице, тем сильнее линейная зависимость между X и Y. Чем ближе значение |ρ _xy | к нулю, тем слабее линейная зависимость между X и Y.
6. Если ρ _xy > 0, то с увеличением одной случайной величины математическое ожидание (среднее значение) другой увеличивается; если ρ _xy < 0, то с увеличением одной случайной величины математическое ожидание (среднее значение) другой уменьшается.
Для случайного вектора (X, Y) ^T вводятся условные математические ожидания M (X / Y = y) и M (Y / X = x). M (X / Y = y) – это математическое ожидание случайной величины X при условии, что Y приняло одно из своих возможных значений y. Аналогично, M (Y / X = x) – это математическое ожидание случайной величины Y при условии, что X приняло одно из своих возможных значений x.
Функцией регрессии Y на X называется зависимость величины M (Y / X = x) от аргумента х. Она характеризует зависимость математического ожидания величины Y от значения, принимаемого величиной X. Аналогично функцией регрессии X на Y называется зависимость величины M (X / Y = y) от аргумента y. Она характеризует зависимость математического ожидания величины X от значения, принимаемого величиной Y. Если обе функции регрессии Y на X и X на Y являются линейными, корреляционная зависимость между случайными величинами X и Y называется линейной. В случае линейной корреляционной зависимости уравнения регрессии – Y на X и X на Y – называются уравнениями линейной регрессии.
Уравнение линейной регрессии Y на X имеет вид

,

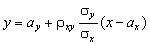(5.4)

а уравнение линейной регрессии X на Y –

.

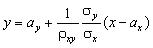(5.5)

5.1.2 Выборочные характеристики двумерного случайного вектора
Пусть (X_i, Y_i), i = 1, 2,..., n – выборка объема n из наблюдений случайного двумерного вектора (X, Y) ^T. Определим оценки числовых характеристик этого вектора. За оценку математических ожиданий a_x и a_y принимаются средние арифметические 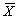и 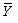(см. формулу (3.2)), за оценку дисперсий σ _x ² и σ _y ² – соответствующие эмпирические дисперсии S_x ² и S_y ², вычисленные по формуле (3.3). Здесь и далее ссылки на формулы с первой цифрой 3 даются на текст типового расчета 10.3.
Несмещенной оценкой ковариации K_xy является величина

.

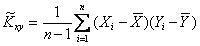(5.6)

Для практических расчетов формулу (5.6) удобно преобразовать к виду:

.

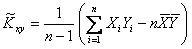(5.7)

Расчет упрощается, если, как и при нахождении оценок параметров одномерной случайной величины, ввести линейную замену (3.6):

При такой замене формула (5.7) принимает вид

.

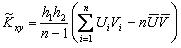(5.9)

Оценку коэффициента корреляции ρ _xy находят по формуле

.

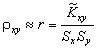(5.10)

Уравнения оценочных (выборочных) прямых регрессии получают по следующим формулам.
Уравнение линейной регрессии Y на X:

.

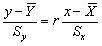(5.11)

Уравнение линейной регрессии X на Y:

.

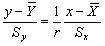(5.12)

Выборочные уравнения прямых регрессии используют для предсказания среднего значения одной переменной по значению другой.

5.1.3 Построение доверительного интервала для коэффициента корреляции. Проверка гипотезы о существовании линейной зависимости
Будем предполагать, что заданная двумерная выборка имеет двумерное нормальное распределение. Тогда доверительный интервал для коэффициента корреляции можно найти по номограммам. В Приложении (см. [1]) приведены такие номограммы (рис. П1) для доверительной вероятности P = 0, 95. По горизонтальной оси номограммы отложены значения выборочного коэффициента корреляции r, по вертикальной оси – значения истинного коэффициента корреляции ρ _xy, числа над кривыми указывают объемы выборок n. Отложив по горизонтальной оси вычисленное значение выборочного коэффициента корреляции, следует подняться над этой точкой вертикально вверх и найти две точки пересечения с кривыми, соответствующими объему заданной выборки. Ординаты этих двух точек являются границами доверительного интервала истинного коэффициента корреляции.
Эти же графики можно использовать для проверки гипотезы H ₀ об отсутствии линейной зависимости между величинами X и Y, т.е. о том, что истинный коэффициент корреляции ρ _xy = 0 при альтернативной гипотезе H ₁: ρ _xy ≠ 0. Гипотеза H ₀ принимается, т.е. линейная зависимость между величинами не существует (с уровнем значимости α = 1 – P), если значение ρ _xy = 0 принадлежит найденному доверительному интервалу. Здесь P – доверительная вероятность при определении доверительного интервала. Гипотеза H ₀ отвергается, т.е. принимается альтернативная гипотеза H ₁ (линейная зависимость между величинами существует), если значение ρ _xy = 0 не принадлежит найденному доверительному интервалу.
Для проверки гипотезы H ₀: ρ _xy = 0 при альтернативной гипотезе H ₁: ρ _xy ≠ 0 можно использовать другой критерий. Гипотеза H ₀ принимается с уровнем значимости α, т.е. линейная зависимость между величинами не существует, если

,

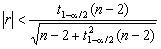(5.13)

в противоположном случае принимается гипотеза H ₁, т.е. предполагается, что линейная зависимость между величинами существует; t _{1– α /2}(n – 2) – квантиль распределения Стьюдента с числом степеней свободы k = n – 2.
Если принята гипотеза о существовании линейной зависимости между случайными величинами, то, зная доверительный интервал для коэффициента корреляции, можно сделать вывод о силе взаимосвязи между X и Y. Если доверительный интервал примыкает к единице или минус единице, то говорят, что связь сильная. Если доверительный интервал примыкает к нулю, то говорят, что связь слабая. Если доверительный интервал расположен примерно посередине интервала (–1; 0) или (0; 1), то говорят, что связь средней величины.

Содержание типового расчета

Заданы результаты n экспериментов, в каждом из которых измерены значения двух величин х и у, т.е. задана выборка объема n, извлеченная из двумерной нормальной генеральной совокупности (Х, Y). По приведенным исходным данным требуется:
– найти оценки характеристик наблюдаемого двумерного случайного вектора;
– найти оценку коэффициента корреляции;
– записать эмпирические уравнения линейной регрессии;
– проверить гипотезу об отсутствии линейной зависимости между величинами X и Y;
– сделать вывод о силе и характере связи между величинами X и Y.