
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Порядок выполнения типового расчета. Примеры
|
|
1. Нахождение оценок числовых характеристик двумерного случайного вектора. Расчет оценки коэффициента корреляции.
Необходимо определить оценки числовых характеристик двумерного случайного вектора. За оценку математических ожиданий α x и α y принимаются средние арифметические 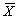 и
и 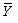 , рассчитанные по формуле (3.23), за оценку дисперсий σ x 2 и σ y 2 – соответствующие эмпирические дисперсии Sx 2 и Sy 2, вычисленные по формуле (3.3). Несмещенная оценка ковариации
, рассчитанные по формуле (3.23), за оценку дисперсий σ x 2 и σ y 2 – соответствующие эмпирические дисперсии Sx 2 и Sy 2, вычисленные по формуле (3.3). Несмещенная оценка ковариации 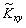 определяется по формуле (5.6).
определяется по формуле (5.6).
Для упрощения расчетов и последующего контроля правильности вычислений следует провести кодировку данных по формуле (5.8). Оценки определяются по формулам (3.7), (3.8), (3.4), (5.9).
Для контроля правильности вычислений весь расчет необходимо повторить при другом начале отсчета. Результаты этих расчетов должны совпасть с точностью до величины возможных ошибок округления. Если результаты расчетов совпадают, определяется оценка коэффициента корреляции по формуле (5.10).
2. Нахождение уравнений линейной регрессии. На этом этапе расчетов требуется записать выборочные уравнения линейной регрессии Y на X и X на Y. На одном чертеже построить прямые регрессии и нанести все экспериментальные точки. Выборочные уравнения линейной регрессии записываются в соответствии с формулами (5.11), (5.12).
3. Построение доверительного интервала для коэффициента корреляции ρ. Проверка гипотезы о существовании линейной зависимости между величинами X и Y.
На этом этапе расчетов требуется найти доверительный интервал для коэффициента корреляции и проверить гипотезу об отсутствии линейной зависимости между величинами X и Y. Уровень значимости α при проверке гипотезы задает преподаватель. Доверительная вероятность P = 1 – α.
Пример выполнения типового расчета.
В первом столбце табл. 1 содержатся измеренные значения величины X – изменения содержания азота в стали при ее выпуске из конвертера по сравнению с начальным содержанием [× 10–4, %]; во втором столбце – значения величины Y (значения начальной концентрации углерода в этой же стали [%]). Найти оценку коэффициента корреляции по этой двумерной выборке. Вычислить выборочные параметры линейной регрессии Y на X и X на Y.
Таблица 1
| Номер эксперимента | X | Y | U | V | U 2 | V 2 | UV |
| – 2, 0 | 0, 11 | – 4 | – 4 | ||||
| 0, 5 | 0, 09 | – 1 | – 1 | ||||
| – 1, 5 | 0, 13 | – 3 | – 9 | ||||
| – 5, 5 | 0, 11 | – 11 | – 11 | ||||
| 3, 5 | 0, 06 | – 4 | – 28 | ||||
| – 1, 0 | 0, 12 | – 2 | – 4 | ||||
| 2, 0 | 0, 08 | – 2 | – 8 | ||||
| 0, 0 | 0, 11 | ||||||
| 1, 5 | 0, 07 | – 3 | – 9 | ||||
| Σ | – | – | – 5 | – 2 | – 74 |
Решение. Вводим линейную замену (5.8), выбирая С 1 = 0, h 1 = 0, 5; С 2 = 0, 10, h 2 = 10–2.
Вычисляем оценки математических ожиданий по формуле (3.7):
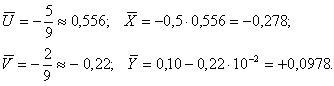
Несмещенные оценки дисперсий находим по формуле (3.8):
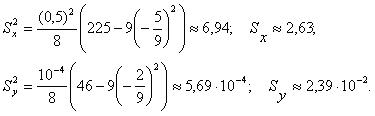
Расчет оценки ковариации проводим по формуле (5.9):
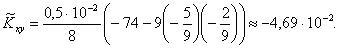
Оценку коэффициента корреляции находим по формуле (5.10):
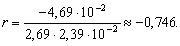
Выборочное уравнение линейной регрессии Y на Х:
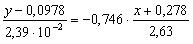 ,
,
или y – 0, 0978 = – 0, 00678 (x + 0, 278).
Выборочное уравнение линейной регрессии Х на Y:
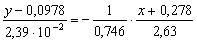 ,
,
или y – 0, 0978 = – 0, 0122 (x + 0, 278).
Прямые регрессии представлены на рис. 1, там же приведены экспериментальные точки.
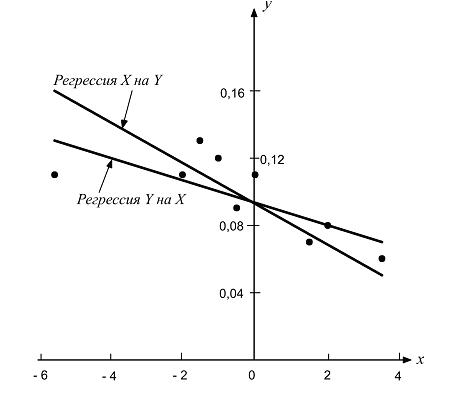
Рис. 1. Зависимость изменения концентрации азота в стали (y)
при выпуске из конвертера от начальной концентрации углерода (x)
По номограммам (см. рис. П1 приложения в [1]) для значения r = – 0, 746 (n = 9) находим интервал: – 0, 95 < ρ < – 0, 14. Так как значение ρ = 0 не принадлежит найденному доверительному интервалу, гипотеза о существовании линейной зависимости не противоречит экспериментальным данным с уровнем значимости α = 0, 05.
Проверим гипотезу об отсутствии линейной зависимости между величинами X и Y с помощью критерия (5.13). По таблице квантилей распределения Стьюдента находим t 0, 975(7) = 2, 365. Вычислим
 .
.
Так как | r | = 0, 746 > 0, 667, принимаем гипотезу о существовании линейной зависимости между величинами X и Y.
Полученные результаты позволяют сделать вывод о том, что с увеличением одной из величин среднее значение другой величины уменьшается. Так как коэффициент корреляции значим, можно пользоваться уравнениями выборочных прямых регрессии для предсказания среднего значения одной переменной по значению другой.