
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прогнозирование продаж с применением аддитивной модели с учетом сезонных колебаний.
|
|
Целью практического занятия является закрепление материала по теме прогнозирование продаж, ознакомление с моделями сезонных колебаний и построение аддитивной модели с учетом сезонных вариаций.
Для аддитивной модели фактическое значение продаж выглядит следующим образом:
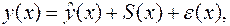 (4.1)
(4.1)
где 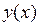 – фактические значения;
– фактические значения; 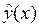 – модель трендовой составляющей прогноза (может быть как линейной, так и нелинейной функцией);
– модель трендовой составляющей прогноза (может быть как линейной, так и нелинейной функцией);  – модель сезонной составляющей (обычно задаётся тригонометрической функцией);
– модель сезонной составляющей (обычно задаётся тригонометрической функцией); 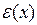 – ошибка аддитивной модели.
– ошибка аддитивной модели.
Особенностью динамического ряда является явно выраженная сезонность, которая учитывается с помощью тригонометрических функций. Так, например, модель тренда может иметь следующий вид:
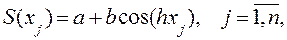 (4.2)
(4.2)
где 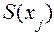 – объем продаж; h – частота колебаний;
– объем продаж; h – частота колебаний; 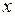 j – текущее время (квартал); a, b – искомые коэффициенты модели.
j – текущее время (квартал); a, b – искомые коэффициенты модели.
Задание 4.1. По данным (табл.4.1), представленным в виде динамического ряда поквартальных продаж (тыс.руб.), необходимо построить траекторию тренда и сделать прогноз на два квартала вперед.
Таблица 4.1
Объем продаж
| Квартал | ||||||||
| Объем продаж |
Результаты расчётов представить в виде графика  , включая прогнозные значения для двенадцатого (x12) и тринадцатого (x13) кварталов.
, включая прогнозные значения для двенадцатого (x12) и тринадцатого (x13) кварталов.
Порядок выполнения задания:
1. Построим график фактических данных продаж для определения частоты колебаний сезонной составляющей (рис.4.1).
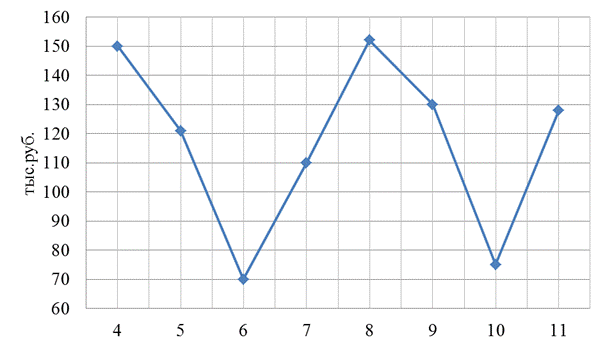
Рис.4.1 Динамика объёма продаж
2. Определим частота сезонных колебаний из следующего соотношения:
1= Cos(2π) = Cos(hr), (4.3)
откуда h = 2π /r, где r – количество кварталов между двумя соседними пиками продаж (период). Первый пик приходится на x4, а второй на x8, т.е. r =4 и, следовательно, имеем h = π /2.
3. Преобразуем нелинейную модель в линейную, для этого необходимо выполнить следующую замену переменных:
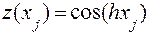 . (4.4)
. (4.4)
После замены переменных получаем новую линейную модель сезонных колебаний:
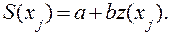 (4.5)
(4.5)
4. Рассчитываем коэффициенты a и b модели (4.5), используя метод наименьших квадратов (2.1) – (2.2). Данные для расчёта коэффициентов представлены в табличной форме (табл.4.2).
Таблица 4.2
Форма таблицы для расчёта параметров модели сезонных колебаний
| Квартал | x | z(x)= cos (π /2x) | y | z2 | zy |
| -1 | -70 | ||||
| -1 | -75 | ||||
| Сумма |
5. Производим обратную замену переменных. Искомая модель сезонных колебаний выглядит следующим образом:
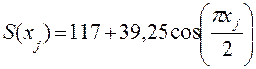 .
.
6. Построим график модели сезонных колебаний S(x) с учётом прогнозных значений для x12 и x13.
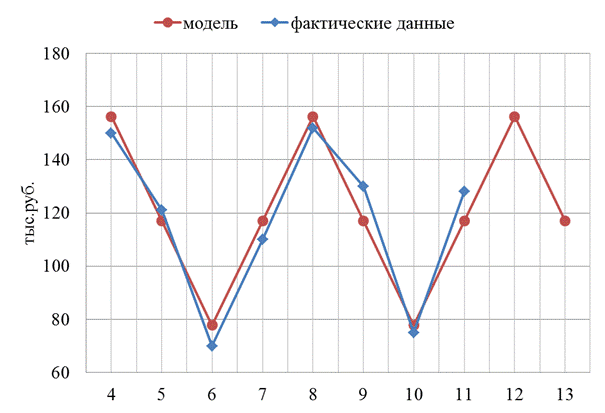
Рис.4.2 Модель сезонных колебаний
Задание 4.2. В таблице 4.3 представлены объёмы продаж (тыс.руб.) за последние 12 кварталов. Необходимо рассчитать аддитивную модель на основании этих данных и прогноз объемов продаж на следующий год. Результаты расчётов представить в виде графика  , включая прогнозные значения.
, включая прогнозные значения.
Таблица 4.3
Объем продаж
| Квартал | ||||||||||||
| Объем продаж |
Порядок выполнения задания:
1. Построим график фактических данных продаж (рис.4.3).
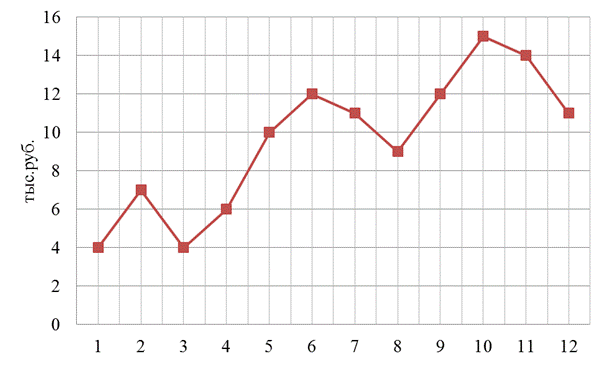
Рис.4.3 Динамика объёма продаж
2. Найдём 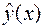 – линейную трендовую составляющую аддитивной модели с помощью МНК.
– линейную трендовую составляющую аддитивной модели с помощью МНК.
3. Рассчитаем 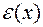 – «невязку» трендовой модели с фактическими данными.
– «невязку» трендовой модели с фактическими данными.
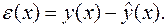 (4.6)
(4.6)
4. Построим график «невязки» для определения частоты сезонных колебаний. Определим частоту сезонных колебаний.
5. Вычислим параметры модели сезонных колебаний. Для этого преобразуем нелинейную модель сезонных колебаний 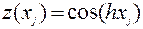 в линейную модель
в линейную модель 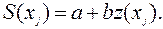
6. Рассчитаем значения аддитивной модели.
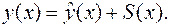 (4.7)
(4.7)
7. Результаты расчётов представим в виде графика 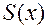 , включая прогнозные значения для следующего года.
, включая прогнозные значения для следующего года.
Задание для самостоятельного решения:
Задание 4.3. В таблице 4.4 представлены объёмы продаж (тыс.руб.) за последние 12 кварталов. Необходимо рассчитать аддитивную модель на основании этих данных и прогноз объёмов продаж на следующий год. Результаты расчётов представить в виде графика, включая прогнозные значения.
Таблица 4.4
Объем продаж
| Квартал | ||||||||||||
| Объем продаж |