Использование в прогнозировании производственных функций

Довольно часто соотношения между социально-экономическими явлениями и процессами приходится описывать нелинейными функциями. Например, производственные функции (зависимость между объемом производства и основными факторами производства) или функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом).

Следует различать модели нелинейные по параметрам и модели нелинейные по переменным.

Для оценки параметров нелинейных моделей применяют два основных подхода:

1. Первый подход основан на линеаризации модели: преобразованием исходных переменных и введением новых, нелинейную модель можно свести к линейной, для оценки параметров которой используется метод наименьших квадратов.

2. Если подобрать соответствующее линеаризующее преобразование не удается, то применяются методы нелинейной оптимизации на основе исходных переменных.

Если модель нелинейна по переменным, то используется первый подход, т.е. вводятся новые переменные, и модель сводится к линейной: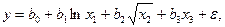

Переходим к новым переменным; 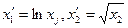и получаем линейное уравнение: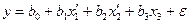

Более сложной проблемой является нелинейность по оцениваемым параметрам. В ряде случаев путем подходящих преобразований эти модели удастся привести к линейному виду. Рассмотрим следующие модели, нелинейные по оцениваемым параметрам:

Степенная (мультипликативная) -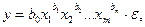

Степенная модель может быть преобразована к линейной путем логарифмирования обеих частей уравнения:

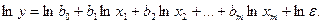(5.20)

и замены переменных: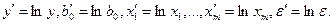

В новых переменных модель запишется следующим образом:

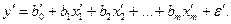(5.21)

Степенные модели получили широкое распространение в эконометрическом моделировании ввиду простой интерпретации параметров, которые представляют собой частные коэффициенты эластичности результативного признака по соответствующим факторным признакам.

Экспонента - .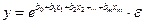

Экспоненциальная модель линеаризуется аналогично:

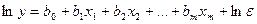. (5.22)

Переходя к новым переменным 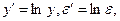получаем линейную регрессионную модель:

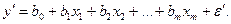(5.23)

Гипербола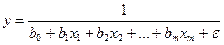

Гиперболическая модель линеаризуется непосредственной заменой переменной y=1/y:

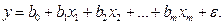(5.24)

Эти функции используются при построении кривых Энгеля, которые описывают зависимость спроса на определенный вид товаров или услуг от уровня доходов потребителей или от цены товара.

Логарифмическая модель: 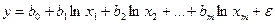линеаризуется путем замены переменных.

При выборе формы уравнения регрессии важно помнить, что чем сложнее функция, тем менее интерпретируемы ее параметры.

Производственная функция (ПФ) - это функциональная модель сферы производства, определяющая «выход» Y по данным о «входе» X.

Различают два основных типа ПФ: производственные функции с взаимозаменяемыми ресурсами; производственные функции с взаимодополняемыми ресурсами (этот тип ПФ здесь не рассматривается). Предположение о взаимозаменяемости ресурсов в производственной функции Y_j=f_j(X_j) означает, что один и тот же объем выпуска продукции может быть получен при разных комбинациях ресурсов, отличающихся тем, что затраты одних ресурсов больше, а других - меньше. Если y=0 при положительных затратах некоторых ресурсов, но при Xs=0, то это означает, что ресурс S абсолютно необходим для производства хотя бы в малых количествах (например, труд, электроэнергия).

Производственные функции могут задаваться не только в аналитической форме, но и в виде таблиц. В качестве примера приведем таблицу выпуска продукции в зависимости от затрат двух видов ресурсов: рабочей силы и средств производства (табл. 5.3).

Таблица 5.3 - Пример табличной ПФ с двумя взаимозаменяемыми ресурсами

Затраты средств производ-
ства Затраты труда

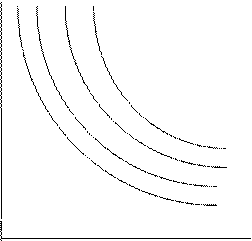
Множество точек, удовлетворяющих уравнению постоянного выпуска f(x)=q, называется изоквантой. На рисунке 5.2 изображено семейство изоквант - кривых в пространстве двух ресурсов. Поскольку X> 0, то все изокванты находятся в неотрицательном ортанте.

X₂

В таблице 5.5. можно указать

комбинацию ресурсов,

принадлежащих изоквантам

Например, комбинации

(60, 10) и (50, 40) дают q=69;

(80, 10) и (60, 40) дают q=110;

(100, 10) и (70, 40) дают q=145.

X₁

Рисунок 5.2 - Семейство изоквант

Процессу эквивалентного замещения одних ресурсов другими соответствует движение вдоль изокванты. Поэтому изокванту называют также кривой замещения.

Производственные функции могут быть статическими и динамическими. В первых не учитывается время как фактор, изменяющий основные характеристики изучаемой зависимости.

Рассмотрим некоторые характеристики функции Кобба-Дугласа:

y=a_0*x₁^a1_*x₂^a2 , (5.25)

где Y - величина общественного продукта; Х₁ - затраты труда; Х₂ -объем производственных фондов (обычно Y и Х₂ измеряются в стоимостных единицах, Х₁ - в человеко-часах или количестве среднегодовых работников).

Определим показатель производительности труда как отношение величины общественного продукта к совокупным затратам труда:

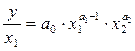. (5.26)

Это выражение характеризует среднюю производительность труда, т.е. показывает среднее количество продукции, приходящееся на единицу отработанного времени. Наряду со средней производительностью труда используют и предельную производительность. Она показывает, сколько дополнительных единиц продукции приносит дополнительная единица затраченного труда. Её уравнение имеет вид (5.27 или 5.28):

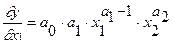(5.27)

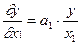. (5.28)

Приняв во внимание, что 0< а₁ < 1, можем видеть, что предельная производительность труда в абсолютном выражении всегда ниже средней производительности.

Другой важной характеристикой производственной функции является показатель эластичности выпуска продукции по затратам труда:

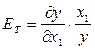. (5.29)

Для функции вида y=a_0*x₁^a1_*x₂^a2 величина Е_Т = а₁. Этот показатель указывает, на сколько процентов увеличится выпуск при увеличении затрат труда на 1 процент.

Аналогично можно определить эластичность выпуска продукции по объему производственных фондов:

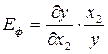(5.30)

(для статической функции Е_Ф = а₂).

Производственная функция позволяет рассчитать потребность в одном из ресурсов при заданном объеме производства и величине другого ресурса.

Например: x₁= 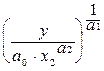; x₂= 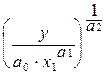. (5.31)

Для производственной функции можно рассчитать и другие показатели:

1. Фондовооруженность труда:

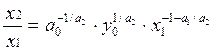. (5.32)

2. Предельную норму замещения ресурса, и в частности, предельную норму замещения затрат труда производственными фондами:

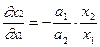. (5.33)

Наибольшее применение в прикладном экономическом прогнозировании имеют два типа ПФ: мультипликативная (функция Кобба-Дугласа) и функция с постоянной эластичностью заменяемости ресурсов (ПЭЗ). Эти функции обладают преимуществами с нескольких точек зрения: 1) они хорошо экономически интерпретируются; 2) имеют небольшое число параметров, что облегчает их статистическую оценку; 3) соответствующие им показатели экономического роста, эффективности, интенсификации имеют удобную аналитическую форму.

В качестве примера использования нелинейной регрессии и линеаризующего преобразования рассмотрим производственную функцию Кобба-Дугласа:

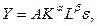(5.34)

где Y – объем производства, К – затраты капитала, L – затраты труда.

Путем логарифмирования обеих частей данную степенную модель можно свести к линейной:

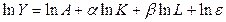. (5.35)

Переходя к новым переменным Y`=lnY, A`=lnA, K`=lnK, L`=lnL, ε `=lnε, получаем линейную регрессионную модель:

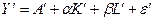, (5.36)

по которой осуществляется регрессионный анализ.

5. Эластичность выпуска продукции. Показатели α и β являются коэффициентами частной эластичности объема производства Y соответственно по затратам капитала К и труда L. Это означает, что с увеличением только затрат капитала (труда) на 1% объем производства возрастает на α % (β %):

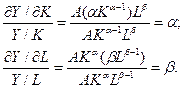(5.37)

4. Эффект от масштаба производства. Если α и β в сумме превышают единицу, то говорят, что функция имеет возрастающий эффект от масштаба производства (это означает, что если К и L увеличиваются в некоторой пропорции, то Y растет в большей пропорции). Если их сумма равна единице, то это говорит о постоянном эффекте от масштаба производства. Если их сумма меньше единицы, то имеет место убывающий эффект от масштаба производства. Например, К и L увеличиваются в 2 раза. Найдем новый уровень выпуска (Y*):

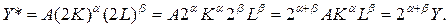(5.38)

Если α +β = 1, 2, то 2^{α +β} =2, 30, а Y увеличивается больше, чем в 2 раза. Если α +β = 1, то 2^{α +β} =2, и Y увеличивается также в 2 раза. Если α +β = 0, 8, то 2^{α +β} =1, 74, а Y увеличивается меньше, чем в 2 раза.

Первоначально математик Чарльз Кобб и экономист Пол Ховард Дуглас представляли функцию в виде 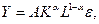т.е. предполагали постоянную отдачу от масштаба производства. Впоследствии это допущение было ослаблено. Если в модели 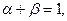то функцию Кобба-Дугласа представляют в виде:

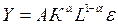или 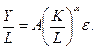(5.39)

Таким образом, переходят к зависимости производительности труда (Y/L) от его капиталовооруженности (K/L). Логарифмируя обе части уравнения, приводим его к линейному виду:

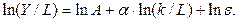(5.40)

Производственная функция Кобба-Дугласа (ПФКД) с учетом технического прогресса имеет вид:

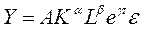, (5.41)

где t — время, параметр 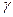— темп прироста объема производства благодаря техническому прогрессу.

Логарифмируя, а затем дифференцируя по t, получим соотношение между темпами прироста конечного продукта y и производственных факторов:

ln y(t)=ln a₀+gt+a_*ln K (t)+b_*ln L (t). (5.42)

P_y= g +a_*P_K +b_* P_{L .} (5.43)

Таким образом, темп прироста конечного продукта есть сумма автономного темпа и взвешенной суммы темпов прироста производственных факторов. Необходимо отметить, что ПФКД с автономным темпом технического прогресса, устраняя многие недостатки рассмотренных ранее модификаций ПФ, не учитывают развития производительных сил (социального прогресса) и средств коммуникаций (информационного прогресса), без которых состав факторов экономического роста в современных условиях является неполным.

Модифицированный вариант производственной функции Кобба-Дугласа с автономным темпом технического прогресса. Для аналитических и прогнозных расчетов на уровне региона авторами предлагается модифицированный вариант производственной функции Кобба-Дугласа с автономным темпом технического прогресса (МПФКД). В нем дифференцируется параметр прогресса g на составные компоненты, характеризующие уровень социального развития региона, технический парк (техническую оснащенность) отраслей регионального хозяйственного комплекса и уровень обеспеченности региона современными коммуникационными средствами. С учетом сказанного, модифицированный вариант производственной функции Кобба-Дугласа с автономным темпом технического прогресса примет следующий вид:

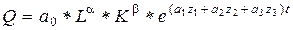(5.44)

или

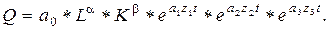(5.45)

где Q - объем выпускаемой продукции за определенный период (за год);

a ₀ - масштабный коэффициент; a₁, a₂, a₃ - числовые параметры;

L - фактор труда, объемный показатель величины трудовых ресурсов;

K - фактор капитала (стоимость основных средств или объем

вложений капитала в производство);

a, b- коэффициенты эластичности при факторах;

z₁ - показатель, характеризующий уровень социального развития (УСР)^*;

z₂ - показатель, характеризующий технический парк отраслей (уровень обновления основных производственных фондов);

z₃ - показатель, характеризующий уровень обеспеченности современными коммуникационными средствами;

t - время.

Величина валового продукта и объем производственных фондов измеряются в стоимостных единицах, а затраты труда - в количестве среднегодовых работников. Уровень социального развития, уровень обновления основных фондов и уровень обеспеченности коммуникациями измеряются в долях единицы, время - в годах.

Такой подход к моделированию региональной экономики позволяет выявить степень влияния на объем производства как технических факторов, так и социальных, и информационных. Логарифмируя МПФКД:

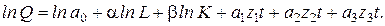(5.46)

а затем дифференцируя ее по t, получим соотношение между темпом прироста валового продукта (P_Q) и темпами прироста производственных факторов:

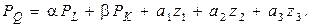(5.47)

Таким образом, темп прироста валового продукта есть сумма взвешенной суммы темпов прироста производственных факторов и автономного темпа прогресса. В свою очередь, автономный темп - взвешенная сумма уровней социального развития, обновления основных фондов и обеспеченности коммуникациями.