
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример выполнения задания в среде Microsoft Excel
|
|
По данным, представленным в таблице 5.3, изучается зависимость балансовой прибыли предприятия торговли Y (тыс. руб.) от следующих факторов:
X1 - объем товарных запасов, тыс. руб.;
X2 - фонд оплаты труда, тыс. руб.;
X3 - издержки обращения, тыс. руб.;
X4 - объем продаж по безналичному расчету, тыс. руб.
Таблица 5.4 - Информация для построения модели регрессии
| Месяц | У | Х1 | Х2 | Х3 | Х4 |
| 41321, 57 | 300284, 10 | 19321, 80 | 42344, 92 | 100340, 02 | |
| 40404, 27 | 49107, 21 | 20577, 92 | 49000, 43 | 90001, 35 | |
| 37222, 12 | 928388, 75 | 24824, 91 | 50314, 52 | 29301, 98 | |
| 37000, 80 | 724949, 11 | 28324, 87 | 48216, 41 | 11577, 42 | |
| 29424, 84 | 730855, 33 | 21984, 07 | 3301, 30 | 34209, 84 | |
| 20348, 19 | 2799881, 13 | 11000, 02 | 21284, 21 | 29300, 00 | |
| 11847, 11 | 1824351, 20 | 4328, 94 | 28407, 82 | 19531, 92 | |
| 14320, 64 | 1624500, 80 | 7779, 41 | 40116, 00 | 17343, 20 | |
| 18239, 46 | 1115200, 93 | 18344, 11 | 32204, 98 | 4391, 00 | |
| 22901, 52 | 1200947, 52 | 20937, 31 | 30105, 29 | 14993, 25 | |
| 27391, 92 | 1117850, 93 | 27344, 30 | 40294, 40 | 104300, 00 | |
| 44808, 37 | 1379590, 02 | 31939, 52 | 42239, 79 | 119804, 33 | |
| 40629, 28 | 588365, 77 | 29428, 60 | 55584, 35 | 155515, 15 | |
| 31324, 80 | 434281, 91 | 30375, 82 | 49888, 17 | 60763, 19 | |
| 34847, 92 | 1428243, 59 | 33000, 94 | 59866, 55 | 8763, 25 | |
| 33241, 32 | 1412181, 59 | 31322, 60 | 49975, 79 | 4345, 42 | |
| 29971, 34 | 1448274, 10 | 20971, 82 | 3669, 92 | 48382, 15 | |
| 17114, 90 | 4074616, 71 | 11324, 93 | 26032, 95 | 10168, 00 | |
| 8944, 94 | 1874298, 99 | 8341, 52 | 29327, 21 | 22874, 40 | |
| 17499, 58 | 1525436, 47 | 10481, 14 | 40510, 01 | 29603, 05 | |
| 19244, 80 | 1212238, 89 | 18329, 90 | 37444, 69 | 16605, 16 | |
| 34958, 32 | 1154327, 22 | 29881, 52 | 36427, 22 | 32124, 63 | |
| 44900, 83 | 1173125, 03 | 34928, 60 | 51485, 62 | 200485, 00 | |
| 57300, 25 | 1435664, 93 | 41824, 92 | 49959, 92 | 88558, 62 |
1. Для заданного набора данных постройте линейную модель множественной регрессии.
2. Оцените точность и адекватность построенного уравнения регрессии. Выделите значимые и незначимые факторы в модели.
3. Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели. Определите коэффициенты эластичности.
4. Получите прогнозные значения прибыли в зависимости от изменения факторов.
Решение
Для получения отчета по построению модели в среде EXCEL необходимо выполнить следующие действия:
1. В меню Сервис выбираем строку Анализ данных. На экране появится окно, в котором выбираем пункт Регрессия. Появляется диалоговое окно, в котором задаем необходимые параметры. Входной интервал Y - диапазон (столбец), содержащий данные со знамениями объясняемой переменной; Входной интервал X - диапазон (столбцы), содержащий данные со значениями объясняющих переменных. Метки - флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет; Константа-ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении регрессии (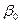 ); Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет; Новый рабочий лист - можно задать произвольное имя нового листа, в котором будет сохранен отчет.
); Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет; Новый рабочий лист - можно задать произвольное имя нового листа, в котором будет сохранен отчет.
Если необходимо получить значения и графики остатков (еi), установите соответствующие флажки в диалоговом окне. Нажмите на кнопку ОК. В отчете о результатах регрессионного анализа («вывод итогов») содержатся три таблицы. Рассмотрим таблицу «Регрессионная статистика» (табл. 5.5).
Таблица 5.5 - Регрессионная статистика
| Множественный R | 0, 905710331 |
| R-квадрат | 0, 820311203 |
| Нормированный R-квадрат | 0, 782481983 |
| Стандартная ошибка | 5705, 632761 |
| Наблюдения |
Множественный R - это 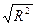 , где R2 - коэффициент детерминации. R-квадрат — это R2. В нашем примере значение R2 = 0, 8203 свидетельствует о том, что изменения зависимой переменной Y (балансовой прибыли) в основном (на 82, 03%) можно объяснить изменениями включенных в модель объясняющих переменных – X1, Х2, X3, X4. Такое значение свидетельствует об адекватности модели. Нормированный R-квадрат - поправленный (скорректированный по числу степеней свободы) коэффициент детерминации. Стандартная ошибка регрессии S =
, где R2 - коэффициент детерминации. R-квадрат — это R2. В нашем примере значение R2 = 0, 8203 свидетельствует о том, что изменения зависимой переменной Y (балансовой прибыли) в основном (на 82, 03%) можно объяснить изменениями включенных в модель объясняющих переменных – X1, Х2, X3, X4. Такое значение свидетельствует об адекватности модели. Нормированный R-квадрат - поправленный (скорректированный по числу степеней свободы) коэффициент детерминации. Стандартная ошибка регрессии S = 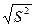 , где S2 =
, где S2 = 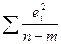 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии); п — число наблюдений (в нашем примере равно 24), т - число объясняющих переменных (в нашем примере равно 4). Наблюдения - число наблюдений п. Рассмотрим результаты дисперсионного анализа (табл. 5.6).
- необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии); п — число наблюдений (в нашем примере равно 24), т - число объясняющих переменных (в нашем примере равно 4). Наблюдения - число наблюдений п. Рассмотрим результаты дисперсионного анализа (табл. 5.6).
Таблица 5.6 - Дисперсионный анализ
| df | SS | MS | F | Значимость F | |
| Регрессия | 705925520, 7 | 21, 68459187 | 7, 27921E-07 | ||
| Остаток | 618530658, 8 | 32554245, 2 | |||
| Итого |
df - degrees of freedom - число степеней свободы связано с числом единиц совокупности п и с числом определяемых по ней констант (m+1). SS - sum of squares - сумма квадратов (регрессионная (RSS-regression sum of squares), остаточная (ESS — error sum of squares) и общая (TSS— total sum of squares), соответственно). MS-mean sum - сумма квадратов на одну степень свободы. F - расчетное значение F-критерия Фишера. Если нет табличного значения, то для проверки значимости уравнения регрессии в целом можно посмотреть Значимость F. На уровне значимости 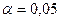 уравнение регрессии признается значимым в целом, если Значимость F < 0.05, и незначимым, если Значимость F
уравнение регрессии признается значимым в целом, если Значимость F < 0.05, и незначимым, если Значимость F 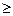 0.05.
0.05.
Для нашего примера имеем следующие значения:
Расчетное значение F -критерия Фишера составляет 21, 68.
Таблица 5.7 - Результаты дисперсионного анализа
| df | SS | MS | F | Значимость F | |
| Регрессия | m = 4 | RSS=2, 82E+09 | RSS/df=7, 06E+08 | 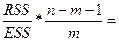 =21, 68
=21, 68
| 7, 28E-07 |
| Остаток | n-m-1=19 | ESS=6, 19E+08 | ESS/df=3, 26E+07 | ||
| Итого | n-1 = 23 | TSS=3, 44E+09 |
Значимость F= 7, 28Е-07, что меньше 0, 05. Таким образом, полученное уравнение в целом значимо. Таблица 5.8 содержит коэффициенты регрессии и оценку их значимости.
Таблица 5.8 - Оценка параметров регрессии
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | 8497, 953555 | 5214, 993986 | 1, 629523175 | 0, 119669485 |
| Переменная X 1 | -0, 001272691 | 0, 001652255 | -0, 770274896 | 0, 450608943 |
| Переменная X 2 | 0, 876317896 | 0, 1565088 | 5, 599160531 | 2, 12344E-05 |
| Переменная X 3 | 0, 005426577 | 0, 097124486 | 0, 05587239 | 0, 956026832 |
| Переменная X 4 | 0, 060582276 | 0, 026352261 | 2, 298940308 | 0, 033024214 |
Таблица 5.9 - Доверительные интервалы для значений коэффициентов
| Нижние 95% | Верхние 95% |
| -2417, 157692 | 19413, 0648 |
| -0, 004730902 | 0, 002185521 |
| 0, 548741111 | 1, 20389468 |
| -0, 197857372 | 0, 208710526 |
| 0, 005426342 | 0, 115738209 |
В таблице приведены значения параметров (коэффициентов) модели, их стандартные ошибки и расчетные значения t-критерия Стьюдента для оценки значимости отдельных параметров модели.
Таблица 5.10 - Оценка коэффициентов регрессии
| Коэффициенты | Стандартная ошибка | t-статистика | Р-Значение | Нижние 95% | Верхние 95% | |
| Y | b0 = 8497, 95 | mb0=5214, 99 | tb0=8497, 95/5214, 99= 1, 6295 | 0, 1197 | -2417, 16 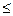 b0 b0 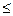 19413, 06 19413, 06
| |
| X1 | b1=-0, 0013 | mb1=0, 0017 | tb1=-0, 0013/0, 0017 = -0, 7703 | 0, 4506 | -0, 0047 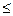 b1 b1 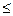 0, 0022 0, 0022
| |
| X2 | b2=0, 8763 | mb2=0, 1565 | tb2=5, 5992 | 2, 12E-05 | 0, 5487 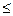 b2 b2 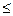 1, 2039 1, 2039
| |
| X3 | b3=0, 00544 | mb3=0, 0971 | tb3=0, 0559 | 0, 9560 | -0, 1978 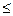 b3 b3 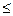 0, 2087 0, 2087
| |
| X4 | b4=0, 0605 | mb4=0, 0263 | tb4=2, 2989 | 0, 0330 | 0, 0054 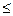 b4 b4 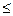 0, 1157 0, 1157
|
Анализ таблицы позволяет сделать вывод о том, что на уровне значимости 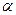 = 0.05 значимыми оказываются лишь коэффициенты при факторах X2 и Х4, так как только для них Р-значение меньше 0, 05. Таким образом, факторы X1 и Х3 не существенны, и их включение в модель нецелесообразно. Поскольку коэффициент регрессии в эконометрических исследованиях имеют четкую экономическую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, как, например -0, 0047
= 0.05 значимыми оказываются лишь коэффициенты при факторах X2 и Х4, так как только для них Р-значение меньше 0, 05. Таким образом, факторы X1 и Х3 не существенны, и их включение в модель нецелесообразно. Поскольку коэффициент регрессии в эконометрических исследованиях имеют четкую экономическую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, как, например -0, 0047 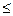 b1
b1 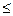 0, 0022. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть. Это также подтверждает вывод о статистической незначимости коэффициентов регрессии при факторах X1 и Х5. Исключим несущественные факторы X1 и Х3 и построим уравнение зависимости Y (балансовой прибыли) от объясняющих переменных X2 и Х4. Результаты регрессионного анализа приведены в таблицах
0, 0022. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть. Это также подтверждает вывод о статистической незначимости коэффициентов регрессии при факторах X1 и Х5. Исключим несущественные факторы X1 и Х3 и построим уравнение зависимости Y (балансовой прибыли) от объясняющих переменных X2 и Х4. Результаты регрессионного анализа приведены в таблицах
Таблица 5.11 - Регрессионная статистика
| Множественный R | 0, 9024465 |
| R-квадрат | 0, 8144098 |
| Нормированный R-квадрат | 0, 7967345 |
| Стандартная ошибка | 5515, 53984 |
| Наблюдения |
Таблица 5.12 - Дисперсионный анализ
| df | SS | MS | F | Значимость F | |
| Регрессия | 46, 076253 | 2, 08847E-08 | |||
| Остаток | 638844774, 1 | 30421179, 72 | |||
| Итого |
Таблица 5.13 - Оценка коэффициентов регрессии
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 5933, 1025 | 2844, 611998 | 2, 085733487 | 0, 0493883 | 17, 40698 | 11848, 798 |
| Переменная X 2 | 0, 9162546 | 0, 132496978 | 6, 915286693 | 7, 834E-07 | 0, 640712 | 1, 1917972 |
| Переменная X 4 | 0, 0645183 | 0, 024940789 | 2, 58686011 | 0, 0172036 | 0, 012651 | 0, 1163856 |
Оценим точность и адекватность полученной модели. Значение R2 = 0, 8144 свидетельствует о том, что вариация зависимой переменной Y (балансовой прибыли) по-прежнему в основном (на 81, 44%) можно объяснить вариацией включенных в модель объясняющих переменных – Х2 и Х4.Это свидетельствует об адекватности модели. Значение поправленною коэффициента детерминации (0, 7967) возросло по сравнению с первой моделью, в которую были включены все объясняющие переменные (0, 7825). Стандартная ошибка регрессии во втором случае меньше, чем в первом (5515 < 5706). Расчетное значение F-критерия Фишера составляет 46, 08 (для первоначальной модели расчетное значение F-критерия Фишера составляло 21, 68). Значимость F = 2, 08847Е-08, что меньше 0, 05. Таким образом, полученное уравнение в целом значимо.
Далее оценим значимость отдельных параметров построенной модели. Из таблицы видно, что теперь на уровне значимости 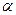 = 0.05 все включенные в модель факторы являются значимыми: Р-значение < 0, 05.
= 0.05 все включенные в модель факторы являются значимыми: Р-значение < 0, 05.
Границы доверительного интервала для коэффициентов регрессии не содержат противоречивых результатов: с надежностью 0.95 (с вероятностью 95%) коэффициент b1 лежит в интервале 0.64 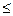 b1
b1 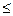 1, 19; с надежностью 0.95 (с вероятностью 95%) коэффициент b2 лежит в интервале 0, 01
1, 19; с надежностью 0.95 (с вероятностью 95%) коэффициент b2 лежит в интервале 0, 01 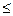 b2
b2 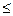 0, 12. Таким образом, модель балансовой прибыли предприятия торговли запишется в следующем виде:
0, 12. Таким образом, модель балансовой прибыли предприятия торговли запишется в следующем виде:
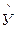 = 5933, 1 + 0, 916*Х2+ 0, 065*Х4.
= 5933, 1 + 0, 916*Х2+ 0, 065*Х4.
Параметры модели имеют следующую экономическую интерпретацию. Коэффициент b1 = 0, 916, означает, что при увеличении только фонда оплаты труда (X2)на 1 тыс. руб. балансовая прибыль в среднем возрастает на 0, 916 тыс. руб., а то, что коэффициент b2 = 0, 065, означает, что увеличение только объема продаж по безналичному расчету (Х4) на 1 тыс. руб. приводит в среднем к увеличению балансовой прибыли на 0, 065 тыс. руб. Как было отмечено выше, анализ Р-значений показывает, что оба коэффициента значимы. Средние коэффициенты эластичности рассчитываются по формуле (5.18).
Эх2=0, 916*22371, 65/29800, 38=0, 688.
Согласно коэффициенту эластичности по второму фактору - рост фонда оплаты труда на 1% приводит к увеличению балансовой прибыли на 0, 688%.
Эх4=0, 065*52220, 1/29800, 38=0, 114.
Согласно коэффициенту эластичности по четвертому фактору - рост объема продаж по безналичному расчету на 1% приводит к увеличению балансовой прибыли на 0, 114%.
Сделаем предположение, что в периоде упреждения размер фонда оплаты труда и объема продаж по безналичному расчету будут равны максимальным значениям за отчетный период: Х2=41824, 92; Х4=200485. Тогда по уравнению регрессии получаем возможное значение 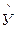 = 57276, 25.
= 57276, 25.