
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основы нечеткой логики
|
|
Нечеткая логика (fuzzy logic) - это надмножество классической булевой логики. Она расширяет возможности классической логики, позволяя применять концепцию неопределенности в логических выводах. Употребление термина " нечеткий" применительно к математической теории может ввести в заблуждение. Более точно ее суть характеризовало бы название " непрерывная логика". Аппарат нечеткой логики столь же строг и точен, как и классический, но вместе со значениями " ложь" и " истина" он позволяет оперировать значениями в промежутке между ними. Говоря образно, нечеткая логика позволяет ощущать все оттенки окружающего мира, а не только чистые цвета.
Нечеткая логика как новая область математики была представлена в 60-х годах профессором калифорнийского университета Лотфи Заде (Lotfi Zadeh). Первоначально она разрабатывалась как средство моделирования неопределенности естественного языка, однако впоследствии круг задач, в которых нечеткая логика нашла применение, значительно расширился. В настоящее время она используется для управления линейными и нелинейными системами реального времени, при решении задач анализа данных, распознавания, исследования операций.
Часто для иллюстрации связи нечеткой логики с естественными представлениями человека об окружающем мире приводят пример о пустыне. Определим понятие " пустыня" как " бесплодная территория, покрытая песком". Теперь рассмотрим простейшее высказывание: " Сахара - это пустыня". Нельзя не согласиться с ним, принимая во внимание данное выше определение. Предположим, что с поверхности Сахары удалена одна песчинка. Осталась ли Сахара пустыней? Скорее всего, да. Продолжая удалять песчинки одну за другой, всякий раз оцениваем справедливость приведенного ранее высказывания. По прошествии определенного промежутка времени песка в Сахаре не останется и высказывание станет ложным. Но после какой именно песчинки его истинность меняется? В реальной жизни с удалением одной песчинки пустыня не исчезает. Пример показывает, что традиционная логика не всегда согласуется с представлениями человека. Для оценки степени истинности высказываний естественный язык имеет специальные средства (некоторые наречия и обороты, например: " в некоторой степени", " очень" и др.). С возникновением нечеткой логики они появились и в математике.
Одно из базовых понятий традиционной логики - понятие подмножества. Подобно этому в основе нечеткой логики лежит теория нечетких подмножеств (нечетких множеств). Эта теория занимается рассмотрением множеств, определяемых небинарными отношениями вхождения. Это означает, что принимается во внимание не просто то, входит элемент во множество или не входит, но и степень его вхождения, которая может изменяться от 0 до 1.
Пусть S - множество с конечным числом элементов, S ={s1, s2,..., sn}, где n - число элементов (мощность) множества S. В классической теории множеств подмножество U множества S может быть определено как отображение элементов S на множество В = {0, 1}:
U: S => В.
Это отображение может быть представлено множеством упорядоченных пар вида:
{si, mui}, iÎ [1, n],
где si - i-й элемент множества S; n - мощность множества S; mUi - элемент множества В = {0, 1}. Если mUi = 1, то si является элементом подмножества U. Элемент " 0" множества В используется для обозначения того, что si не входит в подмножество U. Проверка истинности предиката " skÎ U " осуществляется путем нахождения пары, в которой sk - первый элемент. Если для этой пары mUk =l, то значением предиката будет " истина", в противном случае - " ложь".
Если U - подмножество S, то U может быть представлено n-мерным вектором (mU1, mU2, …, mUn), где i-й элемент вектора равен " 1", если соответствующий элемент множества S входит и в U, и " 0" в противном случае. Таким образом, U может быть однозначно представлено точкой в n-мерном бинарном гиперкубе Вn, В = {0, 1} (рисунок 1).

Рисунок 1 - Графическое представление традиционного множества
Нечеткое подмножество F может быть представлено как отображение элементов множества S на интервал I = [0, 1]. Это отображение определяется множеством упорядоченных пар: {si, mF, (si)}, iÎ [1, n], где si - i-й элемент множества S; n - мощность множества S; mF(si) Î [0, 1] -степень вхождения элемента si в множество F. Значение mF(si), равное 1, означает полное вхождение, mF(si) = 0 указывает на то, что элемент si не принадлежит множеству F. Часто отображение задается функцией mF(x) принадлежности х нечеткому множеству F. В силу этого термины " нечеткое подмножество" и " функция принадлежности" употребляются как синонимы. Степень истинности предиката " skÎ F " определяется путем нахождения парного элементу sk значения mF(sk), определяющего степень вхождения sk в F.
Обобщая геометрическую интерпретацию традиционного подмножества на нечеткий случай, получаем представление F точкой в гиперкубе In, I = [0, 1]. В отличие от традиционных подмножеств точки, изображающие нечеткие подмножества, могут находиться не только на вершинах гиперкуба, но и внутри него (рисунок 2).
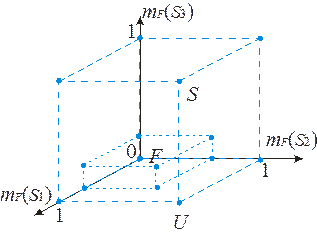
Рисунок 2 - Графическое представление нечеткого множества
Рассмотрим пример определения нечеткого подмножества. Имеется множество всех людей S. Определим нечеткое подмножество Т всех высоких людей этого множества. Введем для каждого человека степень его принадлежности подмножеству Т. Для этого зададим функцию принадлежности mТ(h), определяющую, в какой степени можно считать высоким человека ростом h сантиметров.
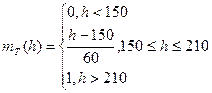 (1)
(1)
где h - рост конкретного человека в сантиметрах.
График этой функции представлен на рисунке 3.
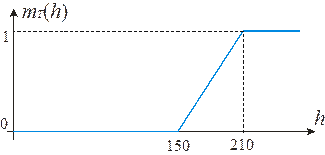
Рисунок 3 - График функции принадлежности rnT(h)
Пусть рост Михаила - 163 см, тогда истинность высказывания " Михаил высок" будет равна 0.21. Использованная в данном случае функция принадлежности тривиальна. При решении большинства реальных задач подобные функции имеют более сложный вид, кроме того, число их аргументов может быть большим.
Методы построения функций принадлежности для нечетких подмножеств довольно разнообразны. В большинстве случаев они отражают субъективные представления экспертов о предметной области. Так, например, кому-то человек ростом 180 см может показаться высоким, а кому-то - нет. Однако часто такая субъективность помогает снизить степень неопределенности при решении слабо формализованных задач. Как правило, для задания функций принадлежности используются типовые зависимости, параметры которых определяются путем обработки мнений экспертов. Представление произвольных функций при реализации автоматизированных систем часто затруднено, поэтому в реальных разработках такие зависимости аппроксимируются кусочно-линейными функциями.
Необходимо осознавать разницу между нечеткой логикой и теорией вероятностей. Заключается она в различии понятий вероятности и степени принадлежности. Вероятность определяет, насколько возможен один из нескольких взаимоисключающих исходов или одно из множества значений. Например, может определяться вероятность того, что утверждение истинно. Утверждение может быть либо истинным, либо ложным. Степень принадлежности показывает, насколько то или иное значение принадлежит определенному классу (подмножеству). Например, при определении истинности утверждения ее возможные значения не ограничены " ложью" и " истиной", а могут попадать и в промежуток между ними. Еще одно различие выражено в математических свойствах этих понятий. В отличие от вероятности для степени принадлежности не требуется выполнение аксиомы аддитивности.