
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Анализ области работоспособности изделия
|
|
Лекция 4 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ НАДЕЖНОСТИ ИЗДЕЛИЯ
1 Представление о состоянии изделия, как о траектории случайного процесса в фазовом пространстве
Для анализа различных вариантов потери машиной или отдельной системой работоспособности целесообразно вначале представить данный процесс в общем виде, как некоторую абстрагированную математическую модель.
Каждое изделие характеризуется некоторыми выходными параметрами (параметрами функционирования) Х1; Х2; …; Хn, которые определяют его состояние и являются случайными функциями времени X(t).
Область работоспособности изделия можно рассматривать, как такое множество G состояний, определяемых значениями параметров Xi при котором отказа не происходит.
Принадлежность данного состояния X (t) множеству G, т. е. X(t) Є G будет означать, что изделие работоспособно. Если любое значение Xi вышло за границу данного множества, то произошел отказ изделия, оно стало неработоспособным.
Если состояние изделия характеризуется несколькими выходными параметрами и будет происходить процесс изменения всех n параметров, то множество G будет связано с n-мерным, так называемым фазовым пространством.
Процесс потери машиной работоспособности может быть представлен в виде траектории случайной функции X(t) в n-мерном фазовом пространстве.
Границы множества G определяются предельно допустимыми значениями параметров Xl max; X2 max;.... Xn max.
Анализ области работоспособности изделия
Рассмотрим область работоспособности изделия в представлениях n-мерного фазового пространства (рисунок 1). Границы области G зависят от требований к изделию. Более высокие требования к его выходным параметрам сужают область работоспособности,
Для одного и того же изделия в зависимости от характера выполняемой работы могут предъявляться различные требования к точности его функционирования. На рисунке 1 показаны две области работоспособности изделия G1 — для обычных и G2 — для более жестких технических условий на параметры изделия.
В области работоспособности изделий следует различать действительную G, которая определяет требуемую работоспособность изделия, и расчетную которая диктуется требованиями ТУ к отдельным параметрам. При оценке работоспособности сложного изделия во многих случаях трудно точно назначить предельное значение отдельных параметров, определяющих предельное состояние изделия в целом.

|
| Рисунок 1 - Области работоспособности и состояний изделия |
Часто о предельном состоянии изделия судят по косвенным показателям, функционально связанным с его работоспособностью. Например, эксплуатационные показатели (выходные параметры) автомобильного двигателя — развиваемая мощность, уровень шума и другие — зависят от износа его сопряжений. О техническом состоянии двигателя часто судят по расходу смазки, что дает весьма приблизительную оценку его работоспособности, так как на этот показатель влияют и многие другие факторы (неисправна вентиляция картера). Поэтому оценка предельного состояния двигателя по расходу смазки не сможет точно выявить область его работоспособности и требуется выбор более точных критериев, оценивающих выходные параметры двигателя.
Из рисунка 1 видно, что между областями действительной G1 и расчетной G’1 работоспособностей изделия имеется разница. В зависимости от соотношения их границ может существовать область неиспользованных возможностей A, когда по ТУ изделие считается потерявшим работоспособность, хотя оно еще может правильно функционировать, и область неучтенных параметров В, когда согласно ТУ можно эксплуатировать изделие, которое в действительности уже стало неработоспособным.
Процесс потери работоспособности характеризуется фазовой траекторией случайного процесса X (t). Например, для процесса Xi(t) i-го изделия при t = t3 считается, что произошел отказ, согласно требований ТУ, а при t = t4 изделие действительно потеряло работоспособность. Область, в которой могут с определенной вероятностью находиться реализации процесса X(t), называется областью состояний. Она определяет возможные состояния изделия, которые оцениваются значениями выходных параметров, т. е. в общем виде вектор-функцией 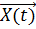 .
.
Для оценки возможного протекания случайного процесса в целом следует применять соответствующие характеристики случайных функций и в первую очередь математическое ожидание М [X (t) ], которое дает оценку того, как в среднем будет протекать процесс потери изделием работоспособности.
При решении задач надежности, большее значение имеет выявление той части области работоспособности Gγ , в которую реализации процесса попадают с заданной вероятностью γ. Границы этой области на рисунке 1 очерчены реализациями Хγ и Х’γ (верхняя и нижняя границы). Например, если γ = 0, 99, то это означает, что с данной вероятностью все реализации попадают в область Gv и с вероятностью всего в 0, 01 они могут проходить через другую часть области G. Такое выделение области Gγ целесообразно для оценки показателей надежности при заданной вероятности безотказной работы.
Совокупность реализаций фазовой траектории случайного процесса X(t) и анализ возможного характера протекания процесса во времени определит область состояний Gt, т. е. такую область в фазовом пространстве, в которую попадают все значения параметров за данный промежуток времени t = Т. Если эта область является частью области работоспособности G, т. е. его подмножеством, то изделие будет устойчиво по отношению к отказам, так как вероятность его возникновения F(t) = 0. Это условие можно записать так же, как
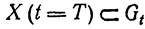 (1)
(1)
т. е. любые значения параметров Х1; Х2; …; Хn определяющие случайный вектор 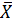 в пределах периода времени t = Т будут принадлежать множеству, которое является подмножеством области работоспособности. Вероятность возникновения отказа наступит лишь после того момента времени, когда условие (1) нарушится и будет возможно пересечение множеств Gt и G. До этого периода времени работа изделия будет протекать в устойчивой зоне по отношению к отказам и запас устойчивости может характеризоваться значением KH — запасом надежности. Поскольку КН (t) является функцией времени, то большое значение имеет оценка скорости израсходования запаса надежности или периода времени, в течение которого его значение станет Кн = 1, и области G и Gt будут соприкасаться.
в пределах периода времени t = Т будут принадлежать множеству, которое является подмножеством области работоспособности. Вероятность возникновения отказа наступит лишь после того момента времени, когда условие (1) нарушится и будет возможно пересечение множеств Gt и G. До этого периода времени работа изделия будет протекать в устойчивой зоне по отношению к отказам и запас устойчивости может характеризоваться значением KH — запасом надежности. Поскольку КН (t) является функцией времени, то большое значение имеет оценка скорости израсходования запаса надежности или периода времени, в течение которого его значение станет Кн = 1, и области G и Gt будут соприкасаться.
Значение t =Тр, при котором станет К (t) = 1, будет являться ресурсом изделия по данному параметру или по их совокупности. При оценке границы области устойчивости могут быть два подхода — вероятностный, когда она ограничивается наибольшим значением параметра, соответствующего заданной вероятности его появления (область Gγ ), и физический (область Gt), когда оценивается наибольшее значение параметра при экстремальных условиях эксплуатации. Если изделие находится в области устойчивости, то гарантируется его безотказная работа. Однако такое состояние достигается, как правило, за счет большого запаса надежности элементов изделия и за счет большой избыточности элементов, что связано со значительными материальными затратами при его производстве.