Собственные числа и собственные векторы матрицы

Найдем фундаментальную систему решений, а следовательно и общее решение.

Рассмотрим систему (5) и запишем ее в операторной форме.

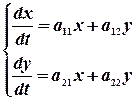
Пусть 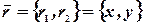- решение системы.

Обозначим дифференциальный оператор через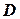

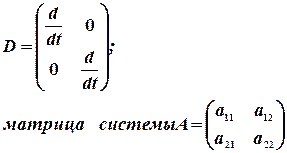
Тогда система (11) имеет вид

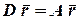
(12)

Или

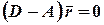
(13)

Система (13) - система однородных уравнений. Для нахождения фундаментальной системы решений найдем собственные векторы оператора 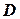и матрицы 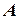, т.е. 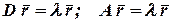- коллинеарный вектор.

Найдем собственные векторы оператора .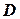

Решим систему 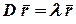, т.е.

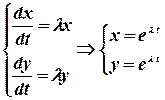, где 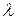- любое.

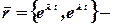собственный вектор .

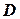Для матрицы 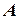собственные числа находятся из уравнения

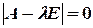
(14)

Находим собственные векторы 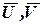из системы

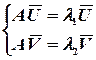
(15)

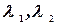собственные числа.

Известно, что если 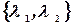спектр оператор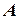а , а 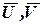- его собственные векторы, то

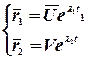
(16)

- решения уравнения (12)

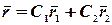
(17)