Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Write(R);. 1) рассуждая так же, как и в предыдущем примере, можно показать, что программа ищет наибольшее значение функции F(t) на интервале от a до b
|
|
END.
Решение:
1) рассуждая так же, как и в предыдущем примере, можно показать, что программа ищет наибольшее значение функции F(t) на интервале от a до b
2) заметим, что выводится не абсцисса, а именно это найденное наибольшее з начение функции:
Write(R);
3) график заданной функции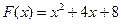 
– это парабола, ветви которой направлены вверх, то есть она имеет точку минимума, но не точку максимума
4) поэтому нужно проверить значения функции на концах отрезка и выбрать из них наибольшее
5) при t=-10 получаем F(t)=68
6) при t=10 получаем F(t)=148
7) таким образом, ответ: 148.
Еще пример задания (Л.А. Тумарина, г. Электросталь):
Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
Var a, b, t, M, R: integer;
Function F(x: integer): integer;
Begin
F: =4*(x-1)*(x-3);
End;
BEGIN
a: =-20; b: =0;
M: =a; R: =F(a);
for t: =a to b do begin
if (F(t)< R)then begin
M: =t;
R: =F(t);
End;
End;
Write(M);
END.
Решение:
1) рассуждая так же, как и в примере 1, определяем, что программа ищет значение t, при котором функция F(t) принимает минимальное значение на интервале от a до b.
2) запишем функцию в виде квадратного трёхчлена:
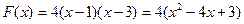
3) график этой функции – парабола, оси которой направлены вверх, поэтому функция имеет минимум
4) найдем абсциссу точки минимума, которая совпадает с абсциссой точки минимума функции
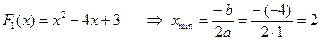
8) однако это значение не входит в интервал [-20; 0], поэтому нужно проверить значения функции на концах отрезка и выбрать из них наименьшее; ответом будет соответствующее значение t.
9) при t=-20 получаем F(-20)=4*(-21)*(-23)=1932
10) при t=0 получаем F(0)= 4*(-1)*(-3)=12, это значение меньше, чем F(-20), поэтому минимум на заданном интервале достигается при t=0
5) таким образом, ответ: 0
Задачи для тренировки [1]:
1) Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
Var a, b, t, M, R: integer;
Function F(x: integer): integer;
Begin
F: =4*(x-5)*(x+3);
End;
BEGIN
a: =-20; b: =20;
M: =a; R: =F(a);
for t: =a to b do begin
if (F(t)< R)then begin
M: =t;
R: =F(t);
End;
End;