
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 7. Основные подходы к измерению социальных признаков
|
|
План лекции:
1. Понятие социологического измерения.
2. Общие принципы теории измерения.
Поскольку социолог имеет дело с массовыми процессами и явлениями, в которых участвует множество людей, социальных групп, институтов и т.д., он по необходимости должен оперировать различными числовыми показателями, выражающими частоты, протяженности и напряженность связи между различными социальными характеристиками, присущими этим процессам и явлениям. Предпосылкой всех операций с количественным выражением социальных характеристик является их первичное измерение.
Измерение – это процедура, с помощью которой объекты измерения сравниваются с некоторым эталоном (шкалой), вследствие чего их свойства, характеристики получают числовое выражение.
Все свойства, с которыми сталкиваются люди, выступают для них либо как количественные, либо как качественные (или атрибутивные). Возраст, заработная плата, цена товара – примеры количественных признаков. Пол, профессия, этническая принадлежность – примеры качественных признаков.
Во многих случаях сведений о наличии или отсутствии какого-либо признака социального свойства бывает недостаточно. Необходимо знание интенсивности данных свойств.
Например, изучение читателей газет требует выяснения не только самого факта чтения тех или иных материалов газеты, но и интенсивности чтения. Социологам, изучающим отношение молодых людей к профессиям, недостаточно выяснить, нравится или не нравится им та или иная профессия. Важно узнать интенсивность положительного или отрицательного отношения к ней.
Когда социолог сталкивается с признаками, которые в повседневной жизни не имеют количественных характеристик, он делает попытку разработать их сам. Эта искусственная операция по приписыванию признакам количественной определенности называется квантификацией (квантификация имеет место, например, тогда, когда преподаватель ставит оценку знаниям студента, когда спортивные судьи приписывают баллы участникам спортивных состязаний, когда туристические маршруты выделяются по степени трудности, когда товароведы определяют сортность продукции, и т.д.)[1].
Проблема измерения – одна из важнейших методологических проблем социологии. Необходимость введения в социологию понятия «измерение» появилась с возникновением социологии как позитивной науки, что было связано с заменой философских методов методами эмпирическими.
Исторически сложились 3 теории измерения.
1. Классическая, описательная, естественнонаучная теория, была первой применена для понятия измерения. Измерение – это сопоставление одной величины с другой при помощи единиц измерения. Это определение предполагает существование объективного предмета с присущими ему объективными свойствами – величинами, такими как длина, ширина. Она также предполагает существование объективных единиц измерения. В социологии и социальной психологии такое определение измерения не подходит, так как в них измеряются свойства индивида, количественных признаков достаточно мало.
2. Репрезентативная теория измерения (РТИ). Основоположником РТИ можно считать известного американского психолога С. С. Стивенса, который первым попытался четко ответить на вопрос: в каком смысле числа, с которыми имеет дело исследователь, получающий информацию от респондента, можно использовать при анализе как действительные числа в математическом смысле этого термина. В основе РТИ лежит представление о том, что измерение – это процедура, с помощью которой объекты измерения, рассматриваемые как носители определенных отношений (эмпирическая система с отношениями), отображаются в некоторую математическую систему с соответствующими отношениями между элементами этой системы (математическая система с отношениями).
3. Формальная (аксиоматическая) теория измерений базируется на аксиоматике, а само измерение в ней – это гомоморфное отображение некоторой системы соотношений в числовую систему соотношений. Считается, что аксиоматическая теория измерений появилась в 1970 г., в работах И. Пфанцагля[2].
В своем онтогенезе процесс измерения проходит пять стадий – соотнесение, исчисление, сравнение, метризацию и структурирование[3].
Соотнесение как качественное различение – первая ступень абстрагирования, при котором внешняя «форма» объекта приобретает самостоятельное значение. Главное число здесь – единица, означающее «единообразие». При различении, которое в современном понимании можно назвать классификацией, «единица» означает и один предмет, и класс однородных предметов независимо от их количества. В данном случае «единица» – символ целого. Простое различение объектов по их наименованию – лишь предпосылка к измерению. Последнее предполагает по меньшей мере исчисление – приписывание однородным классам объектов числового символа.
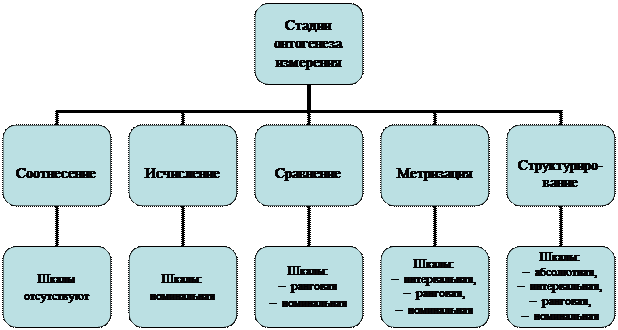
Исчисление – более высокая ступень абстрагирования, предполагающая «отчуждение» и от содержания, и от формы объекта в опоре на кумулятивное (накопительное) мышление, способное соотносить части и целое. Результатом являются количества, обозначаемые числительными, т.е. «пустыми понятиями». Опираясь на них, можно решить ряд задач измерения без соблюдения сложных математических правил.
Исторически исчисление зародилось не из процедуры суммирования единиц, а при делении целого на части, объединении частей в целое. Деление с древнейших времен символизировало распределительные отношения в человеческих общностях.
Любое измерение предполагает соотнесение. Поэтому простое исчисление – это псевдоизмерение, констатация численности. Чтобы измерить объект, его необходимо соотнести (сравнить) с некоторым другим объектом.
Сравнение есть количественное соотнесение с использованием критериев: равно, больше, меньше. Если качественное различение основано на классификации разнородных объектов, то сравнение заключается в количественном соотнесении объектов одного и того же класса или различных классов. Различение количеств по принципу больше–меньше позволяет упорядочить (ранжировать) объекты, соотнеся их с последовательным рядом натуральных чисел, выступающих в качестве символов (рангов).
Всякое измерение есть соотнесение количественных параметров объектов. Первые три стадии онтогенеза «измерения» (точнее, квантификации) основаны на использовании числовых обозначений количеств. Поэтому такая квантификация не нуждается в первоначальной точке отсчета – «нуле».
Понятие «нуля» как символа исходной точки отсчета появляется вместе с зарождением метрического измерения (метризации). Метрические шкалы измеряют не количества, а величины, являющиеся результатом сравнения, но не исчисления.
В метрическом измерении используются два вида шкал – интервальные и абсолютные.
Метризация при помощи интервальной шкалы предполагает:
- наличие эталона измерения (сравнения), в качестве которого выступают не числа, обозначающие количества объектов, а некоторый иной объект, не входящий в класс измеряемых;
- конвенциональный выбор числовых именованных позиций шкалы, делящих ее на интервалы, подчиняющиеся правилу аддитивности;
- конвенциональный выбор «нулевой точки» как исходной для позиций шкалы;
- как положительное, так и отрицательное значения позиции шкалы симметричны относительно нулевой точки.
Метрические шкалы равномерно градуированы.
Все математические операции с величинами, полученными в результате метрического измерения на основе интервальной шкалы, возможны только для классов объектов, измеренных при помощи одного и того же типа шкалы.
Метрические интервальные шкалы взаимно независимы, и не существует правил трансформации одной шкалы в другую. Однако они могут быть применены совместно для многомерных измерений. Подобное измерение осуществляется при помощи индексов. В математике и физике такие индексы называют функциями, а измеряемые первичные величины – аргументами.
Например, для измерения скорости используют сочетание шкал, измеряющих расстояние S, км, и время t, ч: V = S / t.
Абсолютная шкала отличается от интервальной четырьмя свойствами:
- объект измерения и шкала измерения тождественны;
- последняя представляет собой собственно тот же объект измерения, только внутренне структурированный;
- в качестве исходной точки построения позиций шкалы принимается не условная, а абсолютная нулевая точка, за пределами которой объект прекращает свое существование;
- абсолютные шкалы однонаправленны, и их позиции не имеют отрицательных значений;
- все абсолютные шкалы взаимопреобразуемы друг в друга.
Инструментальные различия в онтогенезе измерения можно проиллюстрировать при помощи «аптечных весов»[4].
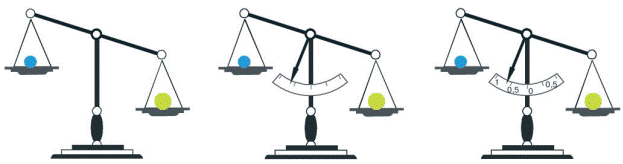
А б в
Соотнесение. Пусть имеется два предмета. Требуется определить, относятся ли они к одному и тому же классу или различаются по весу. Ставим предметы на чаши весов (рис. а), делаем вывод. Для точного вывода здесь нет необходимости в шкалировании, поэтому весы «не нуждаются» ни в стрелке, ни в градуированной шкале.
Ранжирование. Имеем пять предметов. Их необходимо проранжировать строго по весу от наименьшего до наибольшего независимо от «конкретного» веса. Для этого на дуге наносятся метки в произвольном порядке (рис. б) и на оси весов закрепляется указатель (стрелка). Выбирается «на вид» наиболее легкий предмет и относительно него, ориентируясь по меткам на дуге, ранжируются остальные предметы. Если самый легкий предмет находится на левой чаше весов, то при последовательном соотнесении с ним остальных предметов стрелка будет отклоняться влево. Для решения задачи ранжирования не требуется числового градуирования меток дуги (нет необходимости в метрическом измерении).
Метрическое измерение требует точного числового градуирования шкалы (рис. в), для чего используется эталон сравнения. В нашем случае таким эталоном может быть, например, гиря массой 1 кг, а градации шкалы наносятся, скажем, «по 10 г».
Отклонение стрелки при увеличении массы гирь на каждые 10 г обозначается на дуге «меткой» и числовым градуированием. Условная нулевая точка (точка равновесия) располагается в центре дуги. Построенную таким образом шкалу в дальнейшем можно использовать для измерения без помощи гирь.
Числовые значения измерения при помощи шкал в зависимости от используемого индикатора носят или дискретный (прерывный) характер, или непрерывный.
В первом случае говорят об экстенсивных величинах (например, численность имеющих определенный уровень образования, число членов семьи), во втором – об интенсивных (например, оценка респондентами просмотренного фильма по шкале «– 1», «0», «+1», или «понравился», «никакого впечатления», «не понравился»).
Все оценочные суждения, высказываемые респондентами по поводу кого-то или чего-то, носят условно интенсивный характер. Это означает, что интервал между разными уровнями оценок является псевдоинтервалом и при операциях с числами не учитывается, как бы отсутствует, что позволяет назвать шкалы для измерения установок псевдонепрерывными. В естественных науках в качестве интенсивных используют шкалы-эталоны с нормированными числовыми величинами, например шкала температур, времени, т.е. измеряющие процесс. Числовые шкалы-эталоны, измеряющие статическое состояние (рост, вес, возраст, размер дохода и др.), имеют дело с дискретными величинами.
Математическая строгость измерения социальных явлений весьма условна, и здесь правильнее говорить о шкалировании. Это означает, что независимо от того, идет ли речь об экстенсивных или интенсивных величинах, первичным итогом измерения является классификация респондентов по позициям шкал. Без этой процедуры статистический анализ в социологии исключен.
Характер классификации респондентов предопределен используемыми шкалами. В процессе классификации осуществляются две процедуры:
1) структурирование объекта в соответствии со структурой предмета исследования, выявленной в результате операционализации (как бы перенос операциональной модели на объект – носитель социальной проблемы);
2) построение статистических рядов распределений, позволяющих применить для их анализа правила математической статистики.
В последнем случае правила, применимые для анализа тех или иных рядов распределений, предопределены видом используемой шкалы измерения.
Таким образом, на первой стадии измеряются свойства предмета исследования, для чего в качестве источника информации используется единица наблюдения (респондент, семья, группа). В результате мы имеем некоторые числовые значения, или символы (наименования), выступающие в качестве позиций шкал измерения. Классифицируя по этим значениям (или наименованиям) единицы наблюдения, получаем количества. Они всегда обозначаются рациональным числом, их содержания взаимно независимы, а структуры однозначны. Рассмотрим пример.
Относительно 100 респондентов есть две информации:
1) в их составе 60 женщин + 40 мужчин = 100 респондентов;
2) в их составе 60 респондентов намерены участвовать в выборах + 40 респондентов не намерены = 100 респондентов.
Независимо от различия в содержании информации в количественном отношении все числа равнозначны, в результате чего суммы в обоих случаях тождественны. Такое соответствие между величинами называют изоморфизмом.
Для измерения в социологии важен еще один аспект. Так как абсолютное большинство исследований носит выборочный характер, измерение происходит не на всем объекте, а лишь на его части – микромодели. Это рождает проблему соответствия измеренных на микромодели значений некоторых свойств их количественным параметрам в составе общей совокупности. Собственно количественные параметры здесь не могут совпадать хотя бы потому, что численность входящих в общую совокупность элементов многократно превышает численность элементов в микромодели. Речь может идти лишь об эквивалентности, совпадении структур микромодели и объекта по относительным (нормированным) числовым показателям свойств.
Например, если в микромодели из 100 человек 20 % в возрасте до 30 лет, 45 % – в возрасте 31–50 лет и 35 % в возрасте старше 50 лет и таково же процентное соотношение этих возрастных групп в общей совокупности, состоящей, скажем, из 10 000 человек, то между объектом и его микромоделью имеется гомоморфное соответствие (подобие). Такое соответствие крайне важно потому, что в прикладной социологии – это единственный критерий, позволяющий экстраполировать (переносить) результаты измерения свойств микромодели на всю совокупность.
Если на этапе социологического анкетирования происходит измерение, то на этапе классификации – простое исчисление, или объединение респондентов в однородные группы по единому признаку. Подобная процедура осуществляется многократно, в результате чего один и тот же респондент входит во множество групп, каждая из которых образована путем повторного соотнесения респондентов с позициями разных шкал. Именно тот факт, что в образованные по разным признакам классы входят одни и те же респонденты, гарантирует изоморфизм измерения независимо от того, что оно осуществлено на основании разнородных шкал.
Процесс измерения в социологии есть одновременно гомогенизация единиц наблюдения, их приведение к однородному виду (видам) на основании единого признака. Например, выделяя из состава всех жителей Российской Федерации часть совместно по двум критериям «только граждане страны» и только «в возрасте 18 лет и старше», мы получаем функционально однородную (независимо от пола, рода занятий, образования и т.д.) группу, называемую электоратом (избирателями).
Существует целый ряд проблем, связанных с практическим обеспечением того, чтобы измерение отвечало своей сути. Здесь в первую очередь следует назвать проблему взаимодействия объекта измерения и измерителя, «обратное воздействие», оказываемое на людей тестированием каких-то их личностных параметров. Так, известно, что на качество информации, получаемой от респондента, далеко не малое влияние оказывает поведение интервьюера. В то же время известно и не связанное с действием отдельных интервьюеров влияние опросов обществ, мнения на тот социум, из которого произведены соответствующие выборки.
Использованная литература:
1. Горшков М.К., Шереги Ф.Э. Прикладная социология: методология и методы: интерактивное учебное пособие. М.: Институт социологии РАН, 2011, 1 CD ROM.
2. Девятко И.Ф. Логика социологического исследования. М., 1987.
3. Осипов Г.В. Методы измерения в социологии / Г.В. Осипов, Э.П. Андреев. М., 1977.
4. Толстова Ю.Н. Измерение в социологии. М., 1998.
5. Шляпентох В.Э. Проблемы качества социологической информации: достоверность, репрезентативность, прогностический потенциал. М.: ЦСП, 2006. 664 с.
[1] Шляпентох В.Э. Проблемы качества социологической информации: достоверность, репрезентативность, прогностический потенциал. М.: ЦСП, 2006. 664 с. С. 61-62.
[2] Пфанцагль И. Теория измерений. М.: Мир, 1976. 248 с.
[3] Горшков М.К., Шереги Ф.Э. Прикладная социология: методология и методы: интерактивное учебное пособие. М.: Институт социологии РАН, 2011, 1 CD ROM
[4] Там же.
|