
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Структурное тестирование
|
|
Структурное тестирование называют также тестированием по«маршрутам», так как в этомслучае тестовые наборы формируют путем анализа маршрутов, предусмотренных алгоритмом. Под маршрутами при этом понимают последовательности операторов программы, которые выполняются при конкретном варианте исходных данных.
В основе структурного тестирования лежит концепция максимально полного тестирования всех маршрутов программы. Так, если алгоритм программы включает ветвление, то при одном наборе исходных данных может быть выполнена последовательность операторов, реализующая действия, которые предусматривает одна ветвь, а при втором - другая. Соответственно, для программы будут существовать маршруты, различающиеся выбранным при ветвлении вариантом.
Считают, что программа проверена полностью, если с помощью тестов удается осуществить выполнение программы по всем возможным маршрутам передач управления. Однако нетрудно видеть, что даже в программе среднего уровня сложности число неповторяющихся маршрутов может быть очень велико, и, следовательно, полное или исчерпывающее тестирование маршрутов, как правило, невозможно.
Структурный подход к тестированию имеет ряд недостатков. Так тестовые наборы, построенные по данной стратегии:
• не обнаруживают пропущенных маршрутов;
• не обнаруживают ошибок, зависящих от обрабатываемых данных, например, в операторе if (a - b) < eps - пропуск функции абсолютного значения abs проявится только, если а < Ь;
• не дают гарантии, что программа правильна, например, если вместо сортировки по убыванию реализована сортировка по возрастанию.
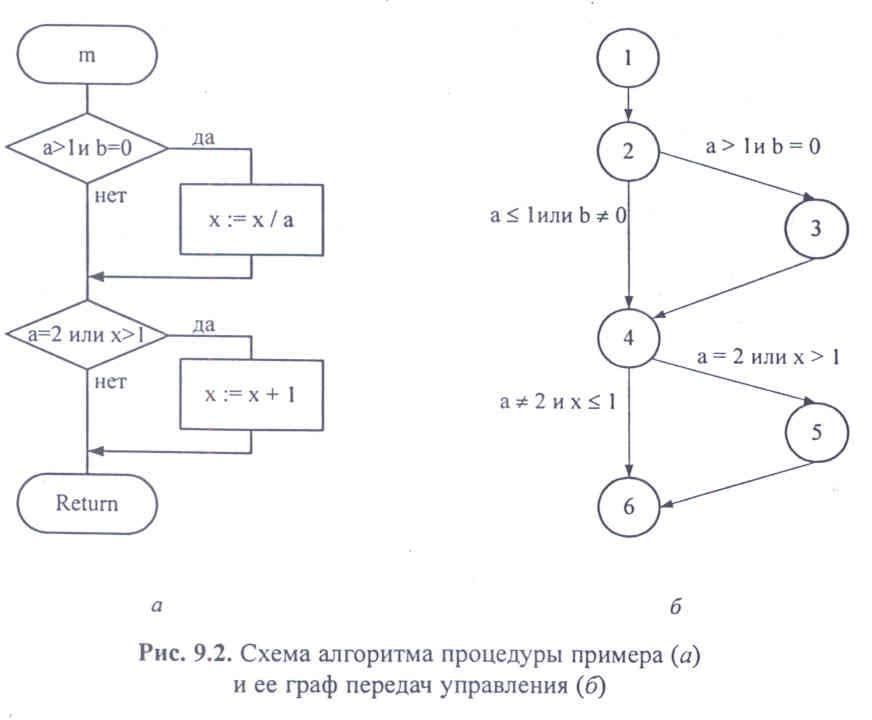
Для формирования тестов программу представляют в виде графа, вершины которого соответствуют операторам программы, а дуги представляют возможные варианты передачи управления. Ниже приведен текст программы, которая определяет значение х в зависимости от значений параметров процедуры. Алгоритм этой программы представлен на рис. 9.2, а, а соответствующий граф передач управления - на рис. 9.2, 6.
Procedure т (а, b: rеа1; var x: real); begin
if (a1) and (b=0) then x: =x/a; if (a=2) or (x> 1) then x: =x+1;
end;
Формирование тестовых наборов для тестирования маршрутов может осуществляться по нескольким критериям:
• покрытие операторов;
• покрытие решений (переходов);
• покрытие условий;
• покрытие решений/условий;
• комбинаторное покрытие условий.
Покрытие операторов. Критерий покрытия операторов подразумевает такой подбортестов, чтобы каждый оператор программы выполнялся, по крайней мере, один раз. Это необходимое, но недостаточное условие для приемлемого тестирования. Поясним сказанное примером.
Для фрагмента, алгоритм и граф которого представлены на рис. 9.2, можно было бы выполнить каждый оператор один раз, задав в качестве входных данных а = 2, b = О, х = 3. Но при этом из второго условия следует, что переменная х может принимать любое значение, и в некоторых версиях языка Pascal это значение проверяться не будет (!).
Кроме того:
• если при написании программы в первом условии указано: (а > 1) or (b = 0), то ошибка обнаружена не будет;
• если во втором условии вместо х > 1 записано х > 0, то эта ошибка тоже не будет обнаружена;
• существует путь 1-2-4-6 (см. рис. 9.2, б), в котором х вообще не меняется и, если здесь есть ошибка, она не будет обнаружена.
Таким образом, хотя при тестировании действительно необходимо задавать исходные данные так, чтобы все операторы программы были выполнены хотя бы один раз, для проверки программы этого явно недостаточно.
Покрытие решений (переходов). Для реализации этого критерия необходимо такоеколичество и состав тестов, чтобы результат проверки каждого условия (т.е. решение) принимал значения «истина» или «ложь», по крайней мере, один раз.
Нетрудно видеть, что критерий покрытия решений удовлетворяет критерию покрытия операторов, но является более «сильным».
Программу, алгоритм которой представлен на рис. 9.2, а, можно протестировать по методу покрытия решений двумя тестами, покрывающими либо пути: 1-2-4-6, 1-2-3-4-5-6, либо пути: 1-2-3-4-6, 1-2-4-5-6, например:
а = 3, Ь = 0, х = 3— путь 1-2-3-4-5-6;
а = 2, b = 1, х = I — путь 1-2-4-6.
Однако путь, где х не меняется, будет проверен с вероятностью 50 %: если во втором условии вместо условия х > 1 записано х < 1, то этими двумя тестами ошибка обнаружена не будет.
Покрытие условий. Критерий покрытия условий является еще более«сильным»посравнению с предыдущими. В этом случае формируют некоторое количество тестов, достаточное для того, чтобы все возможные результаты каждого условия в решении были выполнены, по крайней мере, один раз.
Однако, как и в случае покрытия решений, этот критерий не всегда приводит к выполнению каждого оператора, по крайней мере, один раз. К критерию требуется дополнение, заключающееся в том, что каждой точке входа управление должно быть передано, по крайней мере, один раз.
Программа, алгоритм которой представлен на рис. 9.2, а, проверяет четыре условия:
1) а> 1; 2) Ь = 0; 3) а = 2; 4) х> 1.
Необходимо реализовать все возможные ситуации:
а> 1, а ≥ 1, b = 0, b≠ 0, а = 2, а ≠ 2, х> 1, х ≤ 1.
Тесты, удовлетворяющие этому условию:
а = 2, Ь = 0, х = 4 — путь 1-2-3-4-5-6, условия: 1 - да, 2 - да, 3 - да, 4 - да;
а = 1, b = 1, х = 1 — путь 1-2-4-6, условия: 1 - нет, 2 - нет, 3 - нет, 4 - нет.
Критерий покрытия условий часто удовлетворяет критерию покрытия решений, но не всегда. Тесты критерия покрытия условий для ранее рассмотренных примеров покрывают результаты всех решений, но это случайное совпадение. Например, тесты:
а= 1, b = 0, х = 3 — путь 1-2-3-6, условия: 1 - нет, 2 - да, 3 - нет, 4 - да;
а = 2, b = 1, х = 1 — путь 1-2-3-4-5-6, условия: 1 - да, 2 - нет, 3 - да, 4 - нет
покрывают результаты всех условий, но только два из четырех результатов решений: не выполняется результат «истина» первого решения и результат «ложь» второго.
Основной недостаток метода - недостаточная чувствительность к ошибкам в логических выражениях.
Покрытие решений/условий. Согласно этому методу тесты должны составляться так, чтобы, по крайней мере, один раз выполнились все возможные результаты каждого условия и все результаты каждого решения, и каждому оператору управление передавалось, по крайней мере, один раз.
Анализ, проведенный выше, показывает, что этому критерию удовлетворяют тесты:
а-2, b = 0, х = 4 — путь 1-2-3-4-5-6, условия: 1 - да, 2 - да, 3 - да, 4 - да;
а = 1, Ь = 1, х = 1 — путь 1-2-4-6, условия; 1 - нет, 2 - нет, 3 - нет, 4 - нет.
Комбинаторное покрытие условий. Этот критерий требует создания такого множестватестов, чтобы все возможные комбинации результатов условий в каждом решении и все операторы выполнялись, по крайней мере, один раз.
Для программы, алгоритм которой представлен на рис. 9.1, необходимо покрыть тестами восемь комбинаций:
| 1)а > 1, b = 0; | 5) а = 2, | х> 1; | |
| 2)а > 1, b ≠ 0; | 6) | а = 2, | х ≤ 1; |
| 3)а≤ 1, b = 0; | 7) а ≠ 2, | х> 1; | |
| 4)а≤ 1; b ≠ 0; | 8) | а ≠ 2, х ≤ 1. | |
Эти комбинации можно проверить четырьмя тестами:
а = 2, b = 0, х = 4 — проверяет комбинации (1), (5);
а = 2, b = 1, х = 1 — проверяет комбинации (2), (6);
а = 1, b = 0, х = 2 — проверяет комбинации (3), (7);
а = 1, b = 1, х= 1 — проверяет комбинации (4), (8).
В данном случае то, что четырем тестам соответствует четыре пути, является совпадением. Представленные тесты не покрывают всех путей, например, acd. Поэтому иногда необходима реализация восьми тестов.
Таким образом, для программ, содержащих только одно условие на каждое решение, минимальным является набор тестов, который проверяет все результаты каждого решения и передает управление каждому оператору, по крайней мере, один раз.
Для программ, содержащих вычисления, каждое из которых требует проверки более чем одного условия, минимальный набор тестов должен:
• генерировать все возможные комбинации результатов проверок условий для каждого вычисления;
• передавать управление каждому оператору, по крайней мере, один раз.
Термин «возможных» употреблен здесь потому, что некоторые комбинации условий могут быть нереализуемы. Например, для комбинации k< 0 и к> 40 задать k невозможно.