Способы ОМС по двум линиям положения.

Способы: Аналитический: измеряются навигационные параметры, по замеченным в период измерения координатам, определяем значение счислимых параметров счислимой точки.Вычисляем приращение навигационного параметра, определяем модули градиентов и направление градиентов, рассчитываем перенос линии положения, составляем простые уравнения линий положения и вычисляем разность широт и отшествие по определителям 2 порядка.

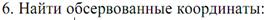
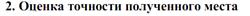
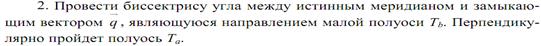
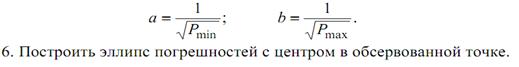
25)Градиенты навигационного параметра.

Любые измерения содержат ошибки, поэтому измерив пеленг, дистанцию или угол и проложив на карте соответствующую изолинию, нельзя считать, что судно будет находиться на этой изолинии. Вычислить возможное смещение изолинии из-за ошибок наблюдений можно, используя понятие градиента функции.

Изобразим две изолинии, соответствующие значениям навигационных параметров U и U + ∆ U (рис. 8.2). На всей изолинии значение функции навигационного параметра остается постоянным, но оно изменится при переходе на другую изолинию. Чем теснее расположены изолинии друг к другу, тем меньше расстояние ∆ n между ними при заданном приращении функции ∆ U, тем быстрее меняется функция в данном районе. Это изменение удобно характеризовать отношением ∆ U/∆ n или вектором g, направленным в сторону возрастания функции по нормали к изолинии. Вектор g называется градиентом. Таким образом, градиентом навигационного параметра назы­вается вектор, направленный по нормали к навигационной изолинии в сторону ее смещения при положительном приращении параметра, причем модуль этого вектора характеризует наибольшую скорость изменения па­раметра в данном месте. Этот модуль равен

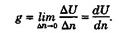
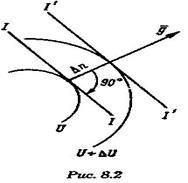
Размерность модуля градиента равна размерности параметра U на линейную величину. Направления вектора градиента и линии положения взаимно перпендикулярны, обозначается направление градиента символом r.

Если при измерении навигационного параметра U допущена ошибка ∆ U и известен градиент, то смещение линии положения параллельно самой себе определяется формулой

Чем больше величина градиента g, тем меньше смещение линии положения при той же ошибке ∆ U, тем точнее будет определение места судна.

Основные понятия и определения теории вероятности. Законы распределения случайных величин.

Частное определение: отношение числа случаев появления события A(m) к общему числу проведённых испытаний (n).Классическое определение: отношение числа испытаний благоприятных событию A(m) к общему числу испытаний (n).Косвенное определение вероятности: в этом случае сложные события разбиваются на несколько простых, вероятность которых подсчитывается частными или классическими, затем вероятность сложного события определяется по вероятностям составляющих его простых событий с использованием теорем сложения и умножения вероятностей.Случайные величины и законы их распределения (СВ): Дискретные: происходят через определённый интервал времени.Непрерывные: непрерывные события.Самый распространенный и наиболее общим законом распределения случайной величины при неограниченном количестве измерений наз-ся закон Гаусса.