Составление нормальных уравнений и способы их решений.

. Составление и решение нормальных уравнений

;

;

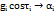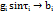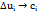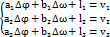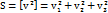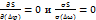. .; . . Тогда,

.

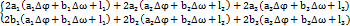Выполнив сложение, получаем систему 2-х нормальных уравнений в обозначениях Гаусса:

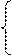[aa]Δ φ +[ab]Δ ω +[al]=0

[ab]Δ φ +[bb]Δ ω +[bl]=0

Так как u_i=a_iΔ φ +b_iΔ ω +l_i, то

[au]=0

[bu]=0

= =

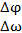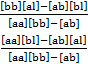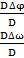
Таким образом получено правило Крамера, где D-главный определитель системы, а D_{Δ φ} и D_{Δ ω} - определители для Δ φ и Δ ω соответственно.Контроль правильности решения получают подстановкой найденных неизвестных в так называемое суммарное уравнение, полученное суммированием нормальных уравнений.([aa]+[ab])Δ φ +([ab]+[bb])Δ ω +([al]+[bl])=0 (22)

Способ решения нормальных уравнений по правилу Крамера при n> 2 становится трудоёмким и не всегда устойчивым при малых значениях D. Другими способами решения системы нормальных уравнений являются: -способ последовательного исключения искомых величин; -способ последовательных приближений (итерации. Первый из них применяется главным образом при неавтоматизированных вычислениях, осуществляемых в ручную или на каркуляторах. Все расчеты выполняются в специальных схемах. Наиболее употребима схема Гаусса-Зейделя, в которой вычисления сводятся к простым однообразным действиям, предусмотрены постоянный контроль правильности вычислений и оценивание точности полученных результатов.Способ итерации легко реализуется на ЭВМ, к недостатку стоит отнести итерационную процедуру, которая не даёт конечного решения, но быстродействие современных ЭВМ снимает этот вопрос.