Определение вида квадратичной формы

Максимизировать целевую функцию:

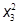Y=21x₁+5x₂+7x₃- -2x₁x₂- - → max

При ограничениях:

x₁+3x₂ ≤ 2

3x₁+x₃ ≤ 0

x_{1, 2, 3} ≥ 0

Возьмем приведённые частные производные частные производные от ЦФ:

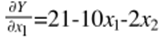
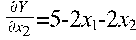
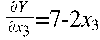
Перепишем целевую функцию:

Y = (0 +10, 5x₁+2, 5x₂+3, 5x₃)*1+

+(10, 5 - 5x₁ - x₂ + 0x₃)*x₁+

+(2, 5 - x₁ - x₂ + 0x₃)*x₂+

+(3, 5 + 0x₁ + 0x₂ - x₃)*x₃

Матрица D:

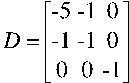
Определяем вид квадратичной формы:

1) Критерий Сильвестра.

Определим миноры:

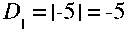
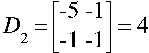
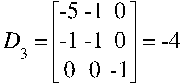
Полученный ряд является знакочередующимся, следовательно, квадратичная форма целевой функции отрицательно определённая.

2) Метод характеристических чисел.

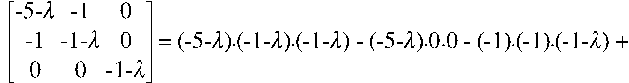
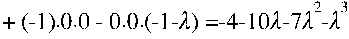
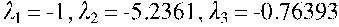
Все корни отрицательные, следовательно, квадратичная форма целевой функции отрицательно определённая.

По результатам исследования квадратичной формы целевой функции можно сделать вывод, что для решения задачи может быть применён квадратичный метод Била.