
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение задачи методом Била
|
|
Допустимое базисное решение:
x4=2-(x1+x2)
x5=0-(3x1+x3)
Целевая функция:
Y = (0 +10, 5x1+2, 5x2+3, 5x3)*1+
+(10, 5 - 5x1 - x2 + 0x3)*x1+
+(2, 5 - x1 - x2 + 0x3)*x2+
+(3, 5 + 0x1 + 0x2 - x3)*x3
Теперь можно сформировать первую таблицу.
Таблица 3.1 – Исходная таблица 1 итерации
| БП | СЧ | X1 | X2 | X3 |
| X1 | ||||
| X2 | ||||
| X3 | ||||
| X4 | -1 | -3 | ||
| X5 | -3 | -1 | ||
| 21/2 | 5/2 | 7/2 | ||
| X1 | 21/2 | -5 | -1 | |
| X2 | 5/2 | -1 | -1 | |
| X3 | 7/2 | -1 |
Так как элементы первой строки нижней части таблицы, стоящие на пересечении с U-ми отсутствуют и элементы, стоящие на пересечении с Х-ми столбцами, положительны, следовательно, решение не является оптимальным, что означает продолжение решения.
U-е столбцы отсутствуют, поэтому в качестве направляющего выбираем столбец, имеющий на пересечении с данной строкой положительный элемент, в данном случае, выберем столбец соответствующий переменной x1. Выбираем направляющую строку, для этого найдём отношение:
 , для
, для  и
и 
Строка, дающая минимум отношений, является направляющей.
Направляющий столбец – x1
Направляющая строка – x5
Элемент, находящийся на пересечении направляющей строки и направляющего столбца – разрешающий (в данном случае он равен -3).
Таблица 3.2 – Промежуточная таблица 1 итерации
| БП | СЧ | X5 | X2 | X3 |
| X1 | -1/3 | -1/3 | ||
| X2 | ||||
| X3 | ||||
| X4 | 1/3 | -3 | 1/3 | |
| X5 | ||||
| -7/2 | 5/2 | |||
| X5 | 21/2 | 5/3 | -1 | 5/3 |
| X2 | 5/2 | 1/3 | -1 | 1/3 |
| X3 | 7/2 | -1 |
Верхнюю часть окончательной таблицы переписываем без изменений из промежуточной в итоговую.
Второй направляющей строкой является строка, пересекающаяся с направляющим столбцом по главной диагонали нижней части таблицы.
Разделив каждый элемент второй направляющей строки промежуточной таблицы на разрешающий элемент, получим соответствующую строку окончательной таблицы. Оставшиеся элементы рассчитаем по формуле:
 ,
,
 - искомый элемент, где i – номер строки, а j – номер столбца (нумерация строк начинается с нижней части таблицы)
- искомый элемент, где i – номер строки, а j – номер столбца (нумерация строк начинается с нижней части таблицы)
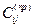 - элемент из промежуточной таблицы, который находиться в ней на месте искомого
- элемент из промежуточной таблицы, который находиться в ней на месте искомого
 - элемент второй разрешающей строки, где к – номер второй разрешающей строки
- элемент второй разрешающей строки, где к – номер второй разрешающей строки
 - элемент первой разрешающей строки, где h – номер первой разрешающей строки.
- элемент первой разрешающей строки, где h – номер первой разрешающей строки.
Таблица 3.3 - Итоговая таблица 1 итерации
| БП | СЧ | X5 | X2 | X3 |
| X1 | -1/3 | -1/3 | ||
| X2 | ||||
| X3 | ||||
| X4 | 1/3 | -3 | 1/3 | |
| X5 | ||||
| -7/2 | 5/2 | |||
| X5 | -7/2 | -5/9 | 1/3 | -5/9 |
| X2 | 5/2 | 1/3 | -1 | 1/3 |
| X3 | -5/9 | 1/3 | -14/9 |
Элементы первой строки нижней части таблицы, стоящие на пересечении с U-ми столбцами не равны нулю или элементы, стоящие на пересечении с Х-ми столбцами, положительны, следовательно решение не является оптимальным.
В качестве начальной таблицы 2-й итерации воспользуемся итоговой таблицей первой итерации.
Рассматриваем первую строку нижней части таблицы без первого элемента.
U-е столбцы отсутствуют или в первой строке нижней части таблицы на пересечении с ними стоят нули, поэтому в качестве направляющего выбирают столбец, имеющий на пересечении с данной строкой положительный элемент.
Направляющий столбец – x2
Направляющая строка – x4
Таблица 3.4 – Промежуточная таблица 2 итерации
| БП | СЧ | X5 | X4 | X3 |
| X1 | -1/3 | -1/3 | ||
| X2 | 2/3 | 1/9 | -1/3 | 1/9 |
| X3 | ||||
| X4 | ||||
| X5 | ||||
| 5/3 | -29/9 | -5/6 | 5/18 | |
| X5 | -59/18 | -14/27 | -1/9 | -14/27 |
| X4 | 11/6 | 2/9 | 1/3 | 2/9 |
| X3 | 2/9 | -14/27 | -1/9 | -41/27 |
Таблица 3.5 – Итоговая таблица 2 итерации
| БП | СЧ | X5 | X4 | X3 |
| X1 | -1/3 | -1/3 | ||
| X2 | 2/3 | 1/9 | -1/3 | 1/9 |
| X3 | ||||
| X4 | ||||
| X5 | ||||
| 26/9 | -83/27 | -11/18 | 23/54 | |
| X5 | -83/27 | -40/81 | -2/27 | -40/81 |
| X4 | -11/18 | -2/27 | -1/9 | -2/27 |
| X3 | 23/54 | -40/81 | -2/27 | -121/81 |
Решение продолжается. Из базиса выводится x1 и вводится x3.
Таблица 3.6 – Промежуточная таблица 3 итерации
| БП | СЧ | X5 | X4 | X1 |
| X1 | ||||
| X2 | 2/3 | -1/3 | -1/3 | |
| X3 | -1 | -3 | ||
| X4 | ||||
| X5 | ||||
| 26/9 | -7/2 | -11/18 | -23/18 | |
| X5 | -83/27 | -2/27 | 40/27 | |
| X4 | -11/18 | -1/9 | 2/9 | |
| X1 | 23/54 | -2/27 | 121/27 |
Таблица 3.7 – Итоговая таблица 3 итерации
| БП | СЧ | X5 | X4 | X1 |
| X1 | ||||
| X2 | 2/3 | -1/3 | -1/3 | |
| X3 | -1 | -3 | ||
| X4 | ||||
| X5 | ||||
| 26/9 | -7/2 | -11/18 | -23/18 | |
| X5 | -7/2 | -1 | -3 | |
| X4 | -11/18 | -1/9 | 2/9 | |
| X1 | -23/18 | -3 | 2/9 | -121/9 |
В итоговой таблице матрица в нижней части таблицы симметрическая, а в первой строке значения, стоящие на пересечении с Х-ми столбцами отрицательные, на пересечении с U-ми столбцами – равны нулю, а следовательно, полученное решение является оптимальным.
Ответ: Y = 26/9, X = (0; 2/3; 0).
3.3 Преобразование нелинейной модели к сепарабельному виду. Аппроксимация нелинейной сепарабельной функции кусочно-линейной функцией
Максимизировать целевую функцию:
Y=21x1+5x2+7x3-  -2x1x2-
-2x1x2-  -
- 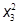 → max
→ max
При ограничениях:
x1+3x2 ≤ 2
3x1+x3 ≤ 0
x1, 2, 3 ≥ 0
Преобразуем нелинейную модель к сепарабельному виду, введя подстановки
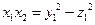 ,
,
где y и z новые переменные.
В задачу также добавятся новые ограничения:

и ограничения для обеспечения неотрицательности:

Определим верхние и нижние границы переменных x1, x2, x3, z, y. Для этого решаем соответствующие задачи линейного программирования c ограничениями:
x1+3x2 ≤ 2
3x1+x3 ≤ 0
x1, 2, 3 ≥ 0
Границы х1:
Y=x1 → min, Y=0;
Y=x1 → max, Y=0;
Границы х2:
Y=x2 → min, Y=0;
Y=x2 → max, Y=2/3;
Границы х3:
Y=x3 → min, Y=0;
Y=x3 → max, Y=0;
Границы y:
Y=y → min, Y=0;
Y=y → max, Y=1/3;
Границы z:
Y=z → min, Y=-1/3;
Y=z → max, Y=0;
Для выбора точек аппроксимации построим графики линеаризуемых функций.

Рисунок 3.1 - График функции F(x)=5x2- 
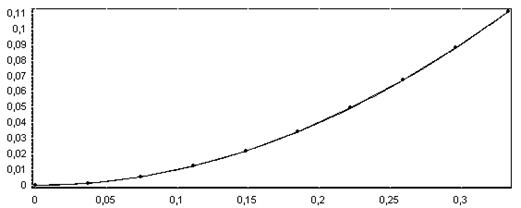
Рисунок 3.2 - График функции F(x)=y2
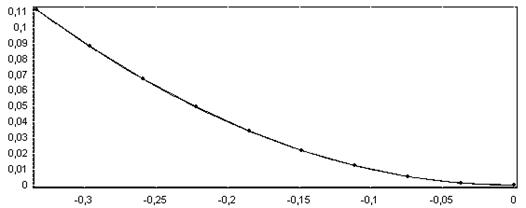
Рисунок 3.3 - График функции F(x)=z2
Точки следует выбрать в соответствии со следующим правилом: чем менее линейна функция на определенном участке, тем выше должна быть плотность точек аппроксимации. Разбиения, принятые при решении данной задачи, приведены в таблице 3.8.
Таблица 3.8 – Сетка аппроксимации
| Переменная | Номера точек | |||||||||
| x1 | ||||||||||
| x2 | 2/27 | 4/27 | 2/9 | 8/27 | 10/27 | 4/9 | 14/27 | 16/27 | 2/3 | |
| x3 | ||||||||||
| y1 | 1/27 | 2/27 | 1/9 | 4/27 | 5/27 | 2/9 | 7/27 | 8/27 | 1/3 | |
| z1 | -1/3 | -8/27 | 7/27 | -2/9 | -5/27 | -4/27 | -1/9 | -2/27 | -1/27 |