
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пояснения к работе. 1.Законы Кирхгофа являются основными соотноше-ниями, на которых базируется расчет электрических цепей.
|
|
1.Законы Кирхгофа являются основными соотноше-ниями, на которых базируется расчет электрических цепей.
Первый закон Кирхгофа:
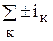 = 0 (1)
= 0 (1)
Алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю.
Правило знаков. При расчете токораспределения в электрической цепи произвольно выбираются условные положительные направления токов в ветвях. Эти направления указываются на схеме стрелками. Ток, вычисленный (или измеренный) в выбранном направлении, может быть либо положительным, либо отрицательным, т.е. iк – алгебраическое число. Если при составлении уравнений по первому закону Кирхгофа токи, утекающие от узла, считать положительными, то токи, подтекающие к узлу, должны браться с дополнительным знаком «минус».
Второй закон Кирхгофа:
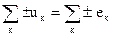 (2)
(2)
Алгебраическая сумма падений напряжения в любом замкнутом контуре равняется алгебраической сумме э.д.с. источников, входящих в тот же контур.
Или алгебраическая сумма напряжений вдоль замкнутого контура равна нулю: U1+U2+U3+U4 = 0
а)
б)

в)
г)

д)

е)
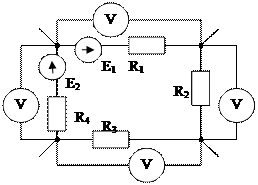
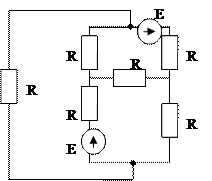
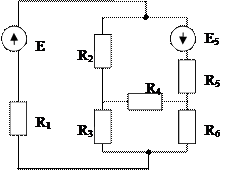
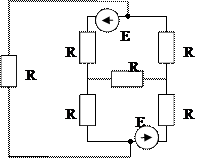
Рис. 1 Схемы электрические принципиальные
Правило знаков. При составлении уравнений по второму закону Кирхгофа выбирается направление обхода контура. Напряжение и к записывается в левую часть равенства, а э.д.с. е к – в правую. При этом и к и е к должны быть взяты с дополнительными знаками «плюс», если их стрелки совпадают с направлениями обхода, и с дополнительными знаками «минус», если стрелки противоположны направлению обхода.
Проверка законов Кирхгофа в данной работе заключается в следующем:
а) собирается конкретная цепь. Варианты схем приведены на рис. 1. Номер схемы и величины э.д.с. задаются преподавателем;
б) на электрической схеме цепи стрелками указываются выбранные направления вычисления токов;
в) с помощью амперметра и вольтметра производится измерение всех токов и напряжений.
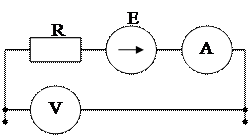

Рис. 2
г) составляются уравнения для всех узлов и контуров цепи по законам Кирхгофа в буквенных обозначениях токов, напряжений и э.д.с. Затем подставляются измеренные значения этих величин и проверяется справедливость равенств (1) и (2);
2. Принцип наложения формулируется следующим образом: ток в К -ой ветви равен алгебраической сумме токов, вызываемых в этой ветви каждой из э.д.с. схемы в отдельности.
Принцип наложения используется в методе расчета, получившем название метода наложения.
Опытная проверка принципа наложения производится в следующем порядке:
а) в цепи, собранной при выполнении пункта 1, отключается один из источников э.д.с., а по месту его действия ставится закоротка (внутренне сопротивление источника считается равным нулю). Производится измерение токов 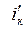 во всех ветвях;
во всех ветвях;
б) проделывается то же самое, что и в пункте 2а, при возвращенном на прежнее место первом источнике и отсоединенном втором (вместо второго источника ставится закоротка). Записываются значения токов 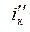
в) по измеренным 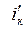 и
и 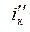 рассчитываются токи iк во всех ветвях при действии обоих источников. Согласно принципу наложения
рассчитываются токи iк во всех ветвях при действии обоих источников. Согласно принципу наложения
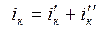
Полученные значения нужно сравнить с измеренными ранее в пункте 1 токами 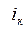 и убедиться в справедливости принципа наложения.
и убедиться в справедливости принципа наложения.
Токи 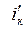 и
и 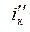 – алгебраические числа; определение их знаков производится в соответствии с правилами, описанными в пункте 1.
– алгебраические числа; определение их знаков производится в соответствии с правилами, описанными в пункте 1.
3.В любой электрической схеме всегда можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы независимо от ее структуры и сложности условно изобразить некоторым прямоугольником. По отношению к выделенной ветви вся схема, обозначенная прямоугольником, представляет собой активный или пассивный двухполюсник.
 |
Двухполюсник при расчете можно заменить эквивалентным генератором, э.д.с. которого равна напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление равно входному сопротивлению двухполюсника.
Метод расчета тока в выделенной ветви, основанный на замене активного двухполюсника эквивалентным генератором, принято называть методом эквивалентного генератора, методом активного двухполюсника или методом холостого хода и короткого замыкания.
Параметры эквивалентного генератора 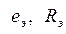 по отношению к одной из ветвей (рис. 3а) определяются следующим образом:
по отношению к одной из ветвей (рис. 3а) определяются следующим образом:

а) б) в)
Рис. 3
а) ветвь размыкается и измеряется напряжение uхх (рис. 3б); ветвь закорачивается через амперметр (рис. 3в), измеряется ток короткого замыкания iк3;
б) параметры эквивалентного генератора определяются соотношениями:
iэ = uxx, Rэ = 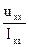
Ток в пассивной ветви находится как
i = 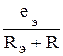 =
= 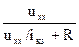
Величины i, uхх, еэ вычисляются (измеряются) в одном направлении (рис. 3)
Результаты измерений и вычислений по пунктам 1, 2, 3, 4 заносятся в таблицу.
Таблица измерений и вычислений
| №№ ветвей | Примечание | |||||||
| е | В | |||||||
| U | В | |||||||
| i | А | |||||||
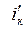
| А | |||||||
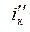
| А | |||||||
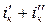
| А | |||||||
| еm | В | |||||||
| ikm | А | |||||||
| ек | В | |||||||
| imk | А | |||||||
| Uхх | В | |||||||
| iкз | А |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Как формулируются законы Кирхгофа?
2. Что означают стрелки тока, напряжения, ЭДС?
3. Как формулируются правила знаков при составлении уравнений Кирхгофа?
4. Как с помощью вольтметра магнитоэлектрической системы определить величину и знак потенциала любой точки цепи по отношению к точке, потенциал которой принят за нулевой?
5. Как формулируется принцип наложения?
6. В чем состоит опытная проверка принципа наложения?
7. Можно ли определить мощность, выделяемую в сопротивлении, пользуясь принципом наложения?
8. Как экспериментально определить параметры схемы эквивалентного генератора?
9. Как формулируется теорема об активном двухполюснике?
10. В чем заключается метод контурных токов?
11. Как определяются собственные и взаимные сопротивления?
12. Как определяются «узловые токи»?
Таблица 1.
| Варианты | Е | Е | R1 | R2 | R3 | R4 | R5 | R6 |
| В | Ом | |||||||
Лабораторная работа № 3
ИССЛЕДОВАНИЕ ФАЗОВОГО РЕЗОНАНСА В ЦЕПИ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ АКТИВНОГО, ИНДУКТИВНОГО И ЕМКОСТНОГО СОПРОТИВЛЕНИЙ
Цель работы: уяснить условия получения резонанса напряжений, экспериментально исследовать явление резонанса напряжений в зависимости от изменения либо реактивного сопротивления, либо частоты исследуемой цепи.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Резонанс напряжений называется такой пассивной электрической цепи переменного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений, при котором входное реактивное сопротивление равно нулю. При резонансе напряжений напряжение на входе цепи совпадает по фазе с током, т.е.
j = yu - yi =0
Условие фазового резонанса через параметры последовательного контура записывается в виде:
хL=xC или 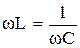 (1)
(1)