
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Программа работы
|
|
1. Собрать схему, изображенную на рис.3 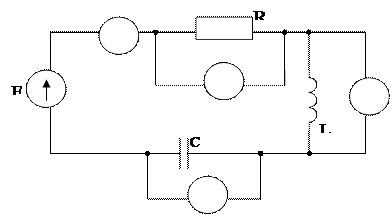
Рис. 3
Примечание: элементы схемы выводятся на экран из «окошка»  ; амперметр и вольтметры из окошка
; амперметр и вольтметры из окошка  .
.
Измерительные приборы перевести из режима «ДС» в режим «АС», дважды нажав на мышку.
При установке значений сопротивлений установить единицу измерения «Ом».
Установить значения ЭДС и сопротивлений согласно варианта (таблица 1).
I вариант
Таблица 1.
| Вариант | ||||||||||
| E, B R, Ом С, мкФ |
2. Рассчитать значение индуктивности, при которой в цепи будет наблюдаться резонанс напряжений.
3. Изменяя индуктивность катушки индуктивности, провести 7 опытов при различном состоянии цепи, включая и резонансный режим. Опыты следует проводить при неизменном входном напряжении. Результаты занести в таблицу 2.
Таблица 2.
| № опыта | L | Измерено | ||||
| U | I | UR | UC | UL | ||
| Гн | В | А | В | В | В | |
| … … |
Продолжение таблицы 2.
| № опыта | Вычислено | |||||||
| Z | xL | xC | x | cosj | P | Q | S | |
| Ом | Ом | Ом | Ом | Вт | ВАр | ВА | ||
| … … |
Расчетные формулы:
Полное сопротивление цепи:
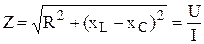
Реактивные сопротивления:
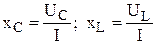
Активная мощность цепи:
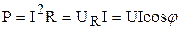
Реактивная мощность цепи:
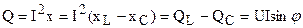
QL - реактивная мощность индуктивности
QC - реактивная мощность емкости
Полная мощность цепи: 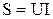
Коэффициент мощности: 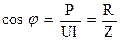
4. По данным опыта и вычисленным параметрам построить кривые зависимостей: UC=f(xL), UL=f(xL); z=f(xL); I=f(xL).
5. Построить векторные диаграммы тока и напряжений для случаев: xL> xC; xL=xC; xL< xC. Все графики и векторные диаграммы выполняются в масштабе.
II вариант
1. Собрать схему, изображенную на рис. 3 Установить значение ЭДС и сопротивлений согласно варианта (таблица 3).
Таблица 3.
| Вариант | ||||||||||
| E, B R, Ом L, Гн | 0, 1 | 0, 15 | 0, 1 | 0, 2 | 0, 15 | 0, 1 | 0, 3 | 0, 2 | 0, 18 | 0, 12 |
2. Рассчитать значение емкости, при которой в электрической цепи будет наблюдаться резонанс напряжений.
3. Изменяя емкость батареи конденсаторов, провести 6-7 опытов при различном состоянии цепи, включая и резонансный режим. Опыты произвести при неизменном входном напряжении. Результаты занести в таблицу 4.
Таблица 4.
| № опыта | С | Измерено | ||||
| U | I | UR | UC | UL | ||
| мкФ | В | А | В | В | В | |
| … … |
Продолжение таблицы 4.
| № опыта | Вычислено | |||||||
| Z | xL | xC | x | P | Q | S | cosj | |
| Ом | Ом | Ом | Ом | Вт | ВАр | ВА | ||
| … … |
4. По данным опыта и вычисленным параметрам построить кривые зависимостей: UC=f(xС), UL=f(xС); z=f(xС); I=f(xС).
5. Построить векторные диаграммы тока и напряжений для случаев: xL> xC; xL=xC; xL< xC.
III вариант
1. Собрать схему, изображенную на рис. 3. Установить значения ЭДС и сопротивлений согласно варианта (таблица 5).
Таблица 5.
| Вариант | ||||||||||
| E, B R, Ом L, Гн С, мкФ | 0, 10 | 0, 12 | 0, 18 | 0, 20 | 0, 16 | 0, 20 | 0, 30 | 0, 25 | 0, 15 0, 22 | 0, 22 |
2. Рассчитать значение частоты, при которой в цепи будет наблюдаться резонанс.
3. Изменяя значение частоты, провести 7 опытов при различном состоянии цепи, включая и резонансный режим. Опыты следует проводить при неизменном входном напряжении. Результаты занести в таблицу 6.
Таблица 6.
| № опыта | f | Измерено | ||||
| U | I | UR | UC | UL | ||
| Гц | В | А | В | В | В | |
| … … |
Продолжение таблицы 6.
| № опыта | Вычислено | |||||||
| Z | xL | xC | x | P | Q | S | cosj | |
| Ом | Ом | Ом | Ом | Вт | ВАр | ВА | ||
| … … |
4. По данным опыта и вычисленным параметрам построить кривые зависимостей: UC=f(w), UL=f(w); z=f(w); I=f(w).
5. Построить векторные диаграммы тока и напряжений для случаев: xL> xC; xL=xC; xL< xC.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В какой цепи может возникнуть резонанс напряжений? Какое условие необходимо для этого?
2. Какими способами возможно получение в колебательном контуре резонанса напряжений?
3. Что такое добротность контура, как она определяется?
4. При каких условиях напряжения на реактивных элементах цепи могут превышать входное напряжение?
5. Чему равняется коэффициент мощности при резонансе?
6. Какой вид имеют резонансные кривые при изменении частоты?
7. Чему равнялось бы при резонансе полное сопротивление цепи, если бы активное сопротивление R было равно нулю?
8. Как изменится полное сопротивление цепи в момент резонанса напряжений при изменении частоты?
9. Как изменится полная мощность цепи при резонансе напряжений?
10. Как строятся треугольники напряжений, сопротивлений, мощностей?
11. Почему при резонансе при резонансе напряжений ток в цепи максимален?
12. Как определить угол сдвига фаз между напряжением, приложенным к цепи и током, протекающим по ней?
Лабораторная работа № 3
ИССЛЕДОВАНИЕ ФАЗОВОГО РЕЗОНАНСА В ЦЕПИ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ АКТИВНОГО, ИНДУКТИВНОГО И ЕМКОСТНОГО СОПРОТИВЛЕНИЙ
(компьютерный вариант, программа Electronic Workbench)
Цель работы: изучить явления, происходящие в электрической цепи переменного тока с параллельным соединением активного, индуктивного и емкостного сопротивлений, экспериментально исследовать резонанс токов.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Резонанс токов – такое состояние пассивной электрической цепи переменного тока с параллельным соединением активного, индуктивного и емкостного сопротивлений, при котором реактивная проводимость цепи и реактивная мощность на зажимах цепи равны нулю. По отношению к внешней цепи двухполюсник ведет себя как активное сопротивление. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением.
Условие фазового резонанса токов:
b=bL – bc = 0, φ =0, или в комплексной форме
Im  =0, где Y=g-jb =
=0, где Y=g-jb = 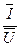
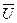 – входное напряжение
– входное напряжение
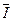 – ток в неразветвленной части цепи.
– ток в неразветвленной части цепи.
Рассмотрим электрическую цепь, состоящую из параллельно включенных ветвей, содержащих активное, индуктивное и емкостное сопротивления (рис. 1). Частный случай
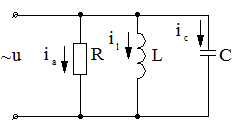
а)

б)
Рис. 1. Цепь с параллельным соединением приемников:
а) электрическая схема цепи;
б) векторная диаграмма при резонансе токов
Явление резонанса характеризуется следующими соотношениями:
1. Полная проводимость минимальна и равна активной составляющей
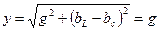 , т.к. b=0.
, т.к. b=0.
Для рассматриваемой цепи
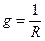
2. Реактивные проводимости
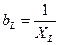 ;
; 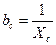
в момент резонанса
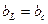 ;
; 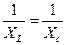
Решаем это уравнение относительно резонансной частоты, определяющей частоту собственных колебаний контура электрической цепи, находим

Резонанс токов можно получить изменением частоты синусоидального напряжения, а также изменением параметров R, L, С
3. Ток в цепи минимален I=Ug, φ =0 (рис. 1 б)
4. Величины активных реактивных составляющих токов в ветвях определяются следующим образом:
Iа=Ug; IL=UbL; Ic=Ubc; IL=Ic;
Рассмотрим электрическую цепь, состоящую из параллельно включенных ветвей, содержащих активное, индуктивное и емкостное сопротивления (рис. 2а).

а)
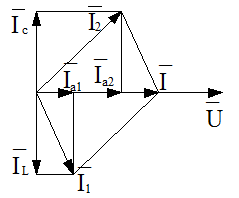
б)
Рис. 2. Цепь с параллельным соединении приемников:
а) электрическая схема цепи;
б) векторная диаграмма при резонансе токов.
В момент резонанса токов:
1. Полная проводимость минимальна и равна активной составляющей
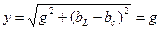 , так как b=0.
, так как b=0.
Для рассматриваемой цепи активная проводимость
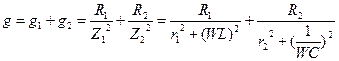
2. Реактивные проводимости
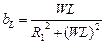 ,
, 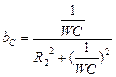 , а так как b=bL–bС= 0,
, а так как b=bL–bС= 0,
то для момента резонанса:
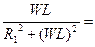
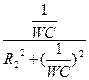
Решая это уравнение относительно резонансной частоты, определяющей частоту собственных колебаний контура электрической цепи, находим:

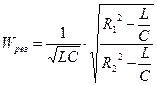
Резонанс токов можно получить изменением частоты синусоидального напряжения, а также изменением параметров r1, r2, L, С приемников. Если R1=R2 =Zb= 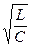 , резонанс токов будет наблюдаться при любой частоте. При соотношении параметров электрической цепи, когда
, резонанс токов будет наблюдаться при любой частоте. При соотношении параметров электрической цепи, когда
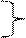
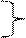 R1 > Zb R1 < Zb
R1 > Zb R1 < Zb
R2 < Zb или R2 > Zb,
нет условия для наступления резонанса.
Резонанс токов возможен в этом случае только при соблюдении неравенства 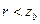 .
.
3. Ток в цепи минимален I=Ug, φ =0 (рис. 1.б).
4. Величины активных и реактивных составляющих токов в ветвях определяется следующим образом:
Ia1=Ug1; Ia2=Ug2; IL= Ic=UbL=Ubc.
При резонансе токов токи I1, I2 ветвей могут быть больше тока I в неразветвленной части.
При изучении явления резонанса токов удобно пользоваться частотными характеристиками, которые достаточно полно рассмотрены в рекомендованной литературе.
В рассматриваемой лабораторной работе режим резонанса токов получают путем изменения собственной частоты электрической цепи за счет изменения величины емкости, либо величины индуктивности.
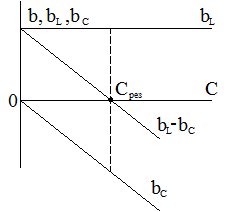
На рис. 3 представлены резонансные кривые при изменении емкости. Из зависимостей, приведенных на рис. 3 а, следует, что изменение емкости С (bс) влечет за собой изменение реактивной проводимостей всей цепи b=bL-bc, а следовательно, и режима работы электрической цепи.
а)
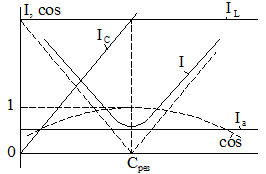
б)
Рис. 3. Резонансные кривые при изменении емкости С:
а) для реактивных проводимостей.
б) для результирующего тока и составляющих тока в отдельных ветвях.
При изменении емкости от 0 до Срез: реактивная проводимость изменяется от bL до 0 и носит индуктивный характер;
Iс увеличивается до величины IL,
Ib неразветвленной цепи уменьшается до своего минимального значения I=Ia=Ug;
Сos φ увеличивается до 1.
Дальнейшее увеличение емкости от Срез до ∞ приведет к тому, что реактивная проводимость электрической цепи вновь будет увеличиваться, приобретая емкостный характер, в пределе стремясь к ∞. Вследствие этого ток I вновь увеличивается от своего минимального значения до некоторой величины 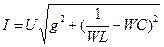
Угол φ изменяется от 0 до arc tg 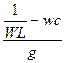
Программа работы.
1 способ.
1. Собрать измерительную цепь, изображенную на рис. 4. Установить значение ЭДС и сопротивлений согласно варианта (таблица 1).
2.
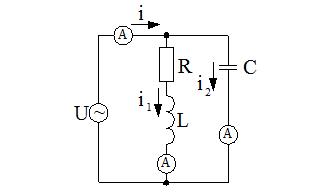
Рис. 4.
Таблица 1.
| вар | ||||||||||
| U1, В | ||||||||||
| R1, Ом | ||||||||||
| L, Гн | 0, 12 | 0, 15 | 0, 17 | 0, 20 | 0, 25 | 0, 3 | 0, 35 | 0, 38 | 0, 45 | 0, 50 |
Установить параметры элементов цепи согласно варианта (частота f=150Гц)
3. Рассчитать значение емкости, при котором реактивная проводимость конденсатора bс будет равна реактивной проводимости катушки bL.
4. Проверить экспериментально правильность проведенных расчетов.
5. При неизменном входном напряжении, постоянных значениях сопротивления (R, L) и частоты f, изменяя емкость, установить различные режимы работы цепи:
дорезонансный – bL > bc
резонансный - bL = bc
послерезонансный - bL < bc
Провести семь опытов. Показания приборов занести в таблицу 2. (∆ С должно быть не менее 20мкф).
6. По данным опытов и вычисленным параметрам построить в масштабе и одних координатных осях кривые
I=f(C), Iс=f(C), IL=f(C), y=f(C), cos φ =f(C)
7. Построить векторные диаграммы напряжения и токов для случаев bL> bc, bL=bc, bL< bc
Таблица 2.
| № | Измерено | ||||
| п/п | U | I | I1 | I2 | С |
| В | А | А | А | мкФ | |
Продолжение таблицы 2.
| № | Вычислено | |||||||||||||
| п/п | Ia | IL | Ip | g | bL | bc | b | g | cosφ | Р | Qc | QL | Q | S |
| А | А | А | См | См | См | См | См | Вт | Вар | Вар | Вар | ВА | ||
Расчетные формулы
Р=I12R=UIa cos φ = 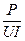 =
= 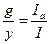
QL= IL2/bL=I12ХL = UIL Ia = I1cosφ 1
Qc=I22 Хс=Ic2/bL=UIc IL = I1sinφ 1
Q=QL-Qc
bL= 
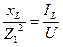 ; bc=
; bc= 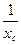 =
= 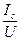 IР=IL-Ic = I sin φ
IР=IL-Ic = I sin φ
g=  , b=bL - bc I=
, b=bL - bc I= 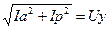
y= 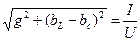 S=UI=
S=UI= 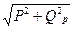
Методические указания
При проведении измерений необходимо перевести все приборы из режима «ДС» в режим «АС».
2 способ.
1. Собрать измерительную цепь, изображенную на рис. 5. Установить значения ЭДС и сопротивлений согласно варианта (таблица 3).
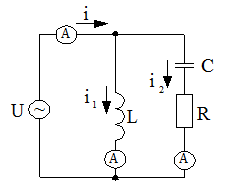
Рис. 5.
Таблица 3
.
| Вар. | ||||||||||
| U, В | ||||||||||
| R, Ом | ||||||||||
| С, мкФ |
Установить параметры элементов цепи согласно варианта (частота задается преподавателем f (50÷ 150 Гц)
2. Рассчитать значение индуктивности, при которой реактивная проводимость индуктивности bL будет равна реактивной проводимости емкости bc.
3. Проверить экспериментально правильность проведенных расчетов.
4. При неизменном входном напряжении, постоянных значениях сопротивлений (R, С) и частоты f, изменяя индуктивность, установить различные режимы работы цепи:
дорезонансный – bL > bс
резонансный - bL = bс
послерезонансный - bL < bс
Провести семь опытов. Показания приборов занести в таблицу 4 (∆ L должно быть не менее 0, 01 Гн)
5. По данным опытов и вычисленным параметрам построить в масштабе и одних координатных осях кривые:
I=f(L), Ic=f(L), IL=f(L), y=f(L), сos φ =f(L).
6. Построить векторные диаграммы напряжения и токов для случаев bL> bc, bL= bc, bL< bc.
Таблица 4.
| № | Измерено | ||||
| п/п | U | I | I1 | I2 | L |
| В | А | А | А | мГн | |
Продолжение таблицы 4.
| № | Вычислено | |||||||||||||
| п/п | Ia | IL | Ip | g | bL | bc | b | y | cosφ | Р | Qc | QL | Q | S |
| А | А | А | См | См | См | См | См | Вт | Вар | Вар | Вар | ВА | ||
Расчетные формулы.
bL= 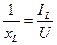 ; bc=
; bc= 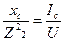 ; b=bL - bc
; b=bL - bc
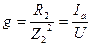 ;
; 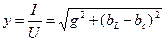
Р=I22R=UIa cosφ = 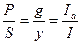
QL=I12XL= 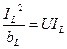 Ia=I2cosφ 2
Ia=I2cosφ 2
QC=IL2XC=  IC = I2sinφ 2
IC = I2sinφ 2
Q=QL-QC IP=IL – IC = I sinφ
S=UI= 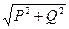 I=
I= 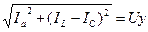
Методические указания.
При проведении измерений необходимо перевести все приборы из режима «ДС» в режим «АС».
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В какой цепи может возникнуть режим резонанса токов?
2. Сформулируйте условие при котором возможен фазовый резонанс токов.
3. Какими способами можно добиться резонанса токов в линейной цепи?
4. Что такое коэффициент мощности приемника?
5. При каком условии токи в индуктивной и емкостной ветвях превышают ток в неразветвленной части цепи?
6. Как изменяется полное сопротивление параллельной цепи при изменении частоты питающего генератора?
7. Почему для повышения коэффициента мощности в энергетике используется режим, близкий к резонансу токов, а не к резонансу напряжений?
8. Потребляется ли от источника при резонансе токов реактивная мощность?
9. Чему равнялся бы при резонансе токов ток неразветвленной части цепи, если бы активное сопротивление к первой ветви (рис. 3) было равно нулю?
10. Практическое значение улучшения коэффициента мощности в производственных условиях.
11. Способы улучшения коэффициента мощности cosφ электротехнической установки.
Лабораторная работа № 3
ЦЕПИ С ИНДУКТИВНО СВЯЗАННЫМИ ЭЛЕМЕНТАМИ.
1. Цель работы.
Экспериментальное определение параметров индуктивных катушек (активного сопротивления, собственной индуктивности) и взаимной индуктивности двух индуктивно связанных элементов. Экспериментальное определение одноименных зажимов катушек. Экспериментальное и теоретическое исследование цепи, содержащей индуктивно связанные элементы.
2. ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
При описании процессов в цепях с индуктивно связанными элементами в первую очередь задают условно-положительные направления токов iк, напряжений Uк на зажимах, потокосцеплений 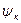 и индуцированных ЭДС
и индуцированных ЭДС 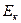 (рис. 1).Под y1 и y2 понимают результирующие потокосцепления:
(рис. 1).Под y1 и y2 понимают результирующие потокосцепления:
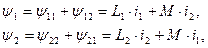
где М - взаимная индуктивность (коэффициент взаимоиндукции), которую обычно считают алгебраической величиной. Это означает, что для выбранной маркировки зажимов катушек величина М положительна, если при выбранных направлениях токов i1 и i2 результирующие потокосцепления y1 и y2 больше соответствующих потокосцеплений самоиндукции y11=L1× i1 и y22=L2i2. И, наоборот, М - отрицательно, если y1 < y11 и y2 < y22. Если же перенести маркировку с одного зажима данной катушки на другой, то знак М изменяется на противоположный. Отсюда следует вывод: нельзя говорить о знаке М без указания тех маркированных зажимов, для которых определяется величина М.
Два зажима, принадлежащие двум разным катушкам, называют одноименными и обозначают одинаковыми значками, если при одинаковом направлении токов относительно одноименных зажимов потокосцепления самоиндукции и взаимной индукции суммируются. Для таких зажимов М > 0. При экспериментальном определении М для одной пары катушек поступают следующим образом. Вначале
зажимы обеих катушек маркируют произвольно и определяют знак М. Если окажется, что М < 0, то изменяют маркировку зажимов одной из катушек, чтобы сделать М величиной положительной.
Уравнения напряжений для индуктивно связанных элементов (рис. 1.б):
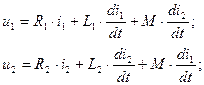
выражения для индуцированных ЭДС:

причем направления величин iк, uк, ек и yк соответствуют принятым на рис.1, а. Однако в практических схемах направления некоторых величин по отношению к маркированным зажимам могут отличаться от принятого. В таком случае следует придерживаться правила: если направление любой величины изменить на противоположное по отношению к принятому, то и знак соответствующего слагаемого в уравнениях надо изменить на противоположный.
Пример: Пусть i2= -i2. Тогда
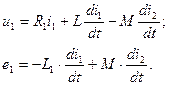
Найти одноименные зажимы катушек можно на основании простого опыта, для которого требуется источник постоянного напряжения и вольтметр магнитоэлектрической системы. К одной из катушек (например, ко второй) присоединяют вольтметр, а к другой подключают источник (рис.2). При замыкании ключа на зажимах 2-й катушки возникает напряжение:

а так как ток i1 возрастает, то di1/dt > 0. Поэтому при отклонении стрелки вольтметра в сторону шкалы (U2 > 0) М -положительно, при отклонении стрелки в противоположную сторону (U2 < 0) M -отрицательно (естественно, для заданной маркировки зажимов катушек). Величину же М определяют на основании другого опыта (рис. 3) при подключении к одной из катушек источника синусоидального напряжения и применении приборов электромагнитной или электродинамической системы. При этом
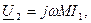
откуда
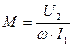 . (1)
. (1)
Величину и знак М определяют и другим способом, используя только один источник (синусоидального напряжения), но проводя два опыта. Для этого зажимы катушек маркируют произвольным образом и соединяют их в одном опыте " условно согласно" (рис.4, а), а в другом - " условно встречно" (рис. 4, б). Тут же заметим, что если маркировка произвольна, то М - величина алгебраическая.
Измерив U, I и Р в обоих опытах, рассчитывают эквивалентные индуктивности схем:
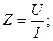
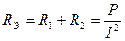 ;
; 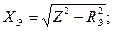
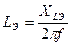 .
.
Так как при согласном включении катушек:
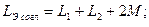
а при встречном:
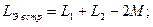
то величину и знак М можно определить по формуле
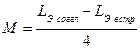 . (2)
. (2)
При магнитной (трансформаторной) связи катушек (рис. 5) важно исследовать зависимость эквивалентных параметров Rэ и Lэ цепи от величины сопротивления нагрузки Rн. В теоретических исследованиях пользуются комплексной схемой замещения (рис. 6).В этой схеме введены обозначения:
Z 1= R1+ jwL1, Z 2=(R2+ Rн)+jwL, Z м=jwM.
Уравнения цепи:
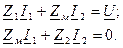
Их можно объединить в одно
 ;
;
позволяющее найти эквивалентное комплексное сопротивление относительно зажимов 1-й катушки:
Z э= 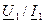 = Z 1-(Z м2/ Z 2)=R1 + jwL 1 -
= Z 1-(Z м2/ Z 2)=R1 + jwL 1 - 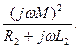
После преобразования получим:
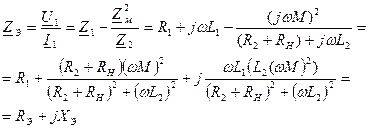
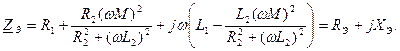
График зависимостей Рэ=Рэ(Рн) и Хэ=Хэ(Рн) приведены на (Рис. 7).
При 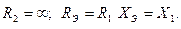
При 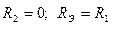 - вторичная цепь не имеет тепловых потерь.
- вторичная цепь не имеет тепловых потерь.
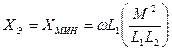 - вторичная цепь оказывает наибольшее размагничивающее действие. Последнюю формулу часто записывают в виде
- вторичная цепь оказывает наибольшее размагничивающее действие. Последнюю формулу часто записывают в виде 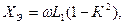
Где 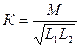 - коэффициент магнитной связи.
- коэффициент магнитной связи.
При этом всегда 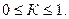
3. Описание экспериментальной установки
Зажимы двух индуктивно связанных катушек выведены на лицевую панель стенда. В левом нижнем углу стенда расположены гнезда регулируемого источника напряжения, справа вверху - гнезда источника регулируемого постоянного напряжения. В качестве вольтметров во всех опытах используется мультиметр, индикатор которого выведен на приборную панель стенда. Токи измеряются комбинированными прибором, мощность - ваттметрам. Оба прибора расположены на столе. В качестве сопротивления нагрузки Рн используются сопротивления резисторов R1, R2, R3, установленные на панели стенда.
4. Проведение эксперимента, обработка данных и анализ результатов.
A. Содержание и порядок проведения работы
1. Пользуясь законом Ома для цепи постоянного тока, определить активные сопротивления R1 и R2 катушек.
2. Используя источник регулируемого синусоидального напряжения, определить собственные индуктивности катушек L1 и L2.
3. Произвольно отмаркировать зажимы катушек и определить
величину и знак взаимной индуктивности М двумя способами, описанными в разделе 2:
а) собирая схемы рис. 2 и З;
б) собирая схемы рис. 4.
4. Собрать схему рис. 5. Изменяя сопротивление нагрузки, снять показания приборов и результаты измерений занести в таблицу 1, каждый раз определяя Rн методом амперметра и вольтметра.
Таблица 1
| Номер опыта | Измерено | Вычислено | ||||||
| На осн.U, I, P | По форм.(3) | |||||||
| RH | U | I | P | RЭ | ХЭ | RЭ | ХЭ | |
| Ом | В | А | Вт | Ом | Ом | Ом | Ом | |
| . | ||||||||
| ∞ |
Б. Указания по обработке экспериментальных данных.
1. Пользуясь формулой (1), вычислить взаимную индуктивность М.
2. Вычислить величину М по формуле (2) на основании расчета эквивалентных индуктивностей.
З. Используя найденные параметры R1, L1, R2, L2 и М, построить векторные диаграммы для согласного и встречного соединений катушек (рис. 4).
4. Произвести вычисления, указанные в таблице, и построить экспериментальные зависимости Rэ=Rэ(Rн) и Хэ = Хэ(Rн).
5. Рассчитать зависимости эквивалентных параметров от Rн по формулам (3) и построить теоретические графики Rэ=Рэ(Рн) и Хэ = Хэ(Rн).
Примечание:
Графики п.п. 4, 5 построить на одном листе миллиметровки
в едином масштабе.
6. Сравнить результаты, полученные в п.п. 4, 5 и сделать выводы.
5. Контрольные вопросы
1). Раскройте физический смысл параметров R и L катушки.
2). Раскройте физический смысл взаимной индуктивности пары катушек.
3). Изобразите схемы и напишите формулы, по которым определяются параметры R и L катушки.
4). Изобразите схемы и приведите формулы, по которым определяются величина и знак взаимной индуктивности двух катушек.
5). Напишите выражения для индуцированных ЭДС и напряжений на зажимах индуктивно связанных катушек.
6). Как маркировка зажимов индуктивно связанных катуше влияет на знаки в слагаемых уравнений для напряжений и индуцированных ЭДС?
7). Как зависят эквивалентные параметры Zэ, Rэ и Хэ схемы рис. 5 от величины сопротивления нагрузки?
8). Почему при встречном включении индуктивно связанных катушек полное сопротивление меньше, чем при согласном?
9).Что такое " емкостный эффект" и при каких условиях он имеет место?
10). Может ли цепь их двух индуктивно связанных друг с другом катушек при встречном соединении вести себя как чисто активное соединение?
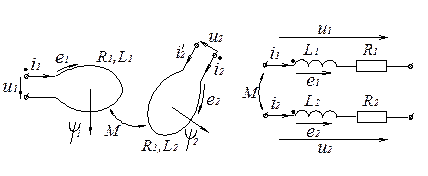 а) б)
а) б)
Рис. 1
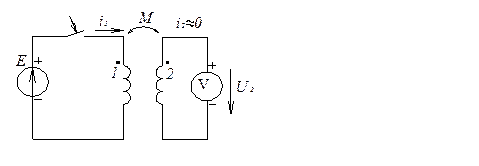 Рис. 2
Рис. 2
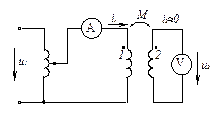
Рис. 3
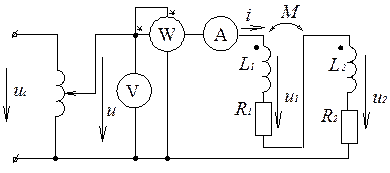 а)
а)
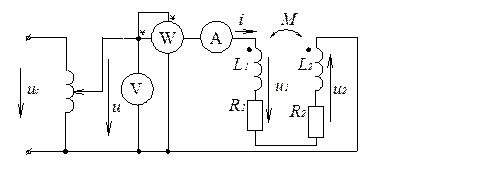 б)
б)
Рис. 4
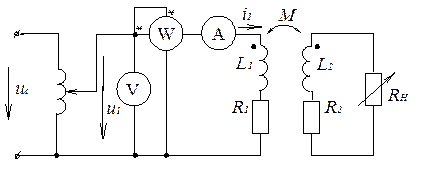 Рис. 5
Рис. 5
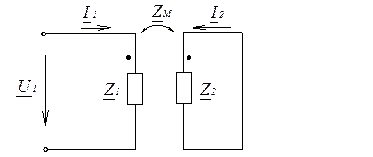
Рис. 6
 Рис.7
Рис.7
ИССЛЕДОВАНИЕ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
С ИНДУКТИВНО СВЯЗАННЫМИ ЭЛЕМЕНТАМИ
(компьютерный вариант)
Цель работы: Расчет коэффициента взаимоиндукции М в цепях переменного тока с последовательным и параллельным соединением катушек и исследование влияния магнитной связи на эквивалентные параметры цепей.
Исходные данные:
| № вар | ||||||||||
| Е, B | ||||||||||
| f, Гц | ||||||||||
| R1, Ом | ||||||||||
| R2, Ом | ||||||||||
| L1, мГн | ||||||||||
| L2, мГн | ||||||||||
| К | 0, 7 | 0, 75 | 0, 78 | 0, 8 | 0, 74 | 0, 8 | 0, 82 | 0, 78 | 0, 84 | 0, 75 |
Программа работы
1.Ознакомиться с основными теоретическими положениями, применяемыми при описании электрических цепей с магнитной связью.
2.Создать схему последовательного согласного включения двух связанных (индуктивно связанных) катушек. Параметры цепи указаны в исходных данных.
3.Рассчитать:
а) коэффициент взаимоиндукции (взаимная индуктивность);
б) комплексные значения тока и падений напряжений на отдельных участках цепи.
4.Построить векторные диаграммы тока и напряжений для согласного включения связанных катушек.
5.Проверка проведенного решения.Собрать схему, соответствующую последовательному согласному включению двух связанных катушек, сравнить показания амперметра со значением тока, полученного в результате проведенных расчетов.
6.Создать схему последовательного встречного включения двух связанных катушек.
7.Рассчитать комплексные значения тока и падений напряжений на отдельных участках цепи.
8.Построить векторные диаграммы тока и напряжений для встречного включения связанных катушек.
9.Проверка проведенного решения.Собрать схему, соответствующую последовательному встречному включению двух связанных катушек, сравнить показания амперметра со значением тока, полученного в результате проведенных расчетов.
10. Создать схему параллельного согласного включения двух связанных катушек. Для известных значений параметров цепи и рассчитанного значения коэффициента взаимоиндукции создать эквивалентную схему замещения (развязка индуктивных связей).
11. Рассчитать значения токов ветвей и падений напряжений на отдельных участках цепи.
12. Построить векторную диаграмму токов и напряжений.
13.Создать схему параллельного встречного включения двух связанных катушек. Для известных значений параметров цепи и рассчитанного значения коэффициента взаимоиндукции создать эквивалентную схему замещения.
14.Рассчитать значения токов ветвей и падений напряжений на отдельных участках цепи.
15.Построить векторную диаграмму токов и напряжений.
16.Экспериментально проверить правильность проведенных расчетов п.11, п.14. Для этого собрать схемы, соответствующие параллельному согласному и параллельному встречному включению двух связанных катушек. Сравнить показания амперметров со значениями токов, полученных в результате расчетов
Контрольные вопросы
Дайте определение параметрам R и L катушки. Поясните физический смысл этих параметров. Нарисуйте схему и напишите формулы, по которым определяются R и L опытным путем при синусоидальном режиме.
Дайте определение и поясните физический смысл параметра M для пары катушек (контуров).
Покажите систему отсчета для 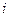 и
и 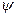 при произвольной маркировке катушек.
при произвольной маркировке катушек.
Напишите выражения для индуктированных ЭДС и напряжений на зажимах каждой из двух индуктивно связанных катушек. Как маркировка влияет на знаки в этих выражениях?
Перечислите и объясните все опыты, проводимые в данной работе по определению величины и знака М. Какие способы вам еще знакомы?
Выведите зависимости 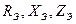 от величины активного сопротивления
от величины активного сопротивления 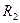
 вторичной цепи для схемы рис. 5.
вторичной цепи для схемы рис. 5.
Почему при встречном включении двух катушек полное сопротивление меньше, чем при согласном включении?
Может ли цепь из двух индуктивно связанных друг с другом катушек при встречном соединении вести себя как чисто активное сопротивление?
Почему при увеличении сопротивления нагрузки (рис. 5) уменьшается ток в первой катушке?
Лабораторная работа № 6
ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЦЕПИ ПРИ СОЕДИНЕНИИ НАГРУЗКИ ЗВЕЗДОЙ.
1. Цель работы
Экспериментальное определение основных соотношений между токами, напряжениями и мощностями в симметричных и несимметричных цепях. Исследование различных режимов работы трехфазной цепи. Выяснение практической роли нейтрального провода.
2. Теоретические положения
а) Для симметричной звезды имеют место соотношения:
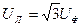 ;
; 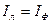 ;
;
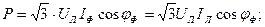
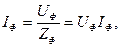
где Zф, Yф -полные сопротивление и проводимость фазы нагрузки.
Модуль фазового угла jф между током и напряжением в фазе нагрузки определяют по измеренным Рф, Uф и Iф:
½ jф ½ =arccos 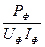 (Pф/Uф·Iф)
(Pф/Uф·Iф)
При выполнении работы вместо индекса " ф " необходимо ставить индекс конкретной фазы нагрузки (а, в, с).
Напряжение смещения нейтрали UnN для несимметричной цепи без нейтрального провода рассчитывают по формуле:
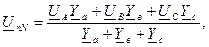
где 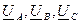 - комплексы фазных напряжений источника:
- комплексы фазных напряжений источника:
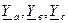 – комплексные проводимости фаз:
– комплексные проводимости фаз:
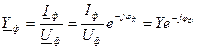 .
.
Ток в нейтральном проводе находят на основании 1-го закона Кирхгофа:
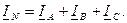
Для измерения мощности в несимметричной трехфазной цепи с доступной нейтральной точкой n нагрузки применяют схему трех ваттметров (рис.9.1). Каждый из ваттметров фиксирует активную мощность фазы: P1=Pa, P2=Pb, P3=Pc. Мощность цепи P=P1+P2+P3.
При симметричной нагрузке достаточно измерить мощность одной фазы, например, Р1, при этом Р=3P1 (схема одного ваттметра).
Для измерения мощности в трех проводной цепи (нейтральный провод отсутствует) применяют схему двух ваттметров независимо от того, симметрична или несимметрична нагрузка (рис.9.2). При этом Р =Р1+Р2 (или Р1’+ Р2’, или Р1’’+ Р2’’). Показания отдельных приборов могут отличаться как по величине, так и по знаку (то есть в общем случае P1¹ P1’¹ P1” и P2¹ P2’¹ P2”) и не соответствуют мощности ни одной из фаз нагрузки.
б) Построение векторно-топографических диаграмм четырех проводной цепи при различных режимах ее работы.
Если пренебречь сопротивлением соединительных проводов, то система линейных напряжений нагрузки совпадает с системой линейных напряжений источника. Поэтому треугольник векторов линейных напряжений нагрузки остается неизменным при любых режимах работы цепи, и построение всех векторных диаграмм следует начинать с построения треугольника векторов линейных напряжений. Точки n и N совпадают, так как сопротивление нейтрального провода близко к нулю.
Рассмотрим различные режимы работы цепи.
1)Нагрузка фаз активная равномерная.


 Принимая начальную фазу фазного напряжения источника
Принимая начальную фазу фазного напряжения источника  равной нулю, откладываем вектор фазного напряжения вдоль по-ложительного направления вещественной оси. Вектор
равной нулю, откладываем вектор фазного напряжения вдоль по-ложительного направления вещественной оси. Вектор 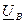 строим отстающим от вектора
строим отстающим от вектора  на угол 120° вектор
на угол 120° вектор 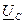 - опережающим вектор
- опережающим вектор  на 120. Векторы линейных напряжений источника получаем как геометрическую разность векторов соответствующих фазных напряжений:
на 120. Векторы линейных напряжений источника получаем как геометрическую разность векторов соответствующих фазных напряжений: 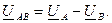
Векторы фазных токов совпадают по направлению с векторами фазных напряжении. Ток нейтрального провода равен нулю. В итоге получаем диаграмму, показанную на рис.9.3.
2)Нагрузка фаз симметричная (резистивно-емкостная).
В отличие от случая 1) векторы фазных токов опережают векторы соответствующих фазных напряжений на фазовый угол j рассчитываемый по данным эксперимента. В остальном построение, диаграммы аналогично случаю 1). Диаграмма приведена на рис.9.4.
3)Нагрузка несимметричная резистивно-емкостная.

 Допустим, что не симметрия образована отключением конденсатора в фазе в. Тогда вектор фазного тока
Допустим, что не симметрия образована отключением конденсатора в фазе в. Тогда вектор фазного тока 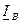 совпадает по направлению с вектором
совпадает по направлению с вектором 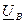 , векторы фазных токов
, векторы фазных токов  и
и 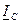 , как и в случае 2), опережают соответствующие векторы
, как и в случае 2), опережают соответствующие векторы  и
и 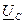 на угол j. Не симметрия нагрузки приводит к появлению тока в нейтральном проводе, вектор которого строим как геометрическую сумму фазных токов (рис. 9.5).
на угол j. Не симметрия нагрузки приводит к появлению тока в нейтральном проводе, вектор которого строим как геометрическую сумму фазных токов (рис. 9.5).
4)Обрыв фазы симметричной резистивной нагрузки.

 Предположим, что обрыв произошел в фазе в. Ток
Предположим, что обрыв произошел в фазе в. Ток 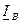 и напряжение
и напряжение 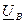 этой фазы равны нулю, а фазные напряжения
этой фазы равны нулю, а фазные напряжения  и
и 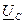 и токи
и токи  и
и 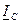 остаются такими же, как и в случае 1). Так как обрыв фазы приводит к несимметрии нагрузки, то появляется ток в нейтральном проводе
остаются такими же, как и в случае 1). Так как обрыв фазы приводит к несимметрии нагрузки, то появляется ток в нейтральном проводе  Диаграмма токов и напряжении приведена на рис. 9.6.
Диаграмма токов и напряжении приведена на рис. 9.6.
в) Построение векторно-топографических диаграмм трех-проводной цепи при различных режимах работы.
В трехфазной цепи без нейтрального провода между нейтралями источника и нагрузки возникает напряжение смещения:
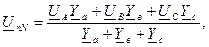
следовательно, положение точки n на векторной диаграмме изменяется при изменении проводимости хотя бы одной из фаз. Соответственно изменяются и фазные напряжения и фазные токи нагрузки. По этой причине соединение фаз приемника звездой без нейтрального провода не применяют, если заранее известно, что нагрузка несимметрична.
Рассмотрим различные режимы работы трех п