Реферат. Моделі поведінки фірми

на тему:

Моделі поведінки фірми

Виконала

студентка групи ПМа- 41

Ільків Юлія

Львів – 2015

Математичне моделювання виробницва повинно враховувати як внутрішні умови виробничих процесів, так і повнішій умови, що обумо­влюються довкіллям підприємства - середовищем прямої дії та сере­довищем непрямої дії. Це приводить до складного комплексу моделей діяльності підприємства (фірми) у тих чи інших умовах, при тих чи інших припущеннях. Велику роль тут грає увага до раціоналізації поведінки підприємства - об’єктивний бік оптимізації процесів вироб­ництва, оптимальне розподілення коштів та використання різних фак­торів виробництва.

Найбільш поширеними є моделі рівноваги фірми, що будуються на таких припущеннях.

1. Технологічні умови виробництва описуються виробничою фун­кцією 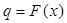. що має певний комплекс властивостей.

2. Враховується можливість фірми впливати на ціну своєї продукції та на ціни факторів виробництва. При цьому виникають різні моделі пов’язані, як з умовами досконалої конкуренції, так із різними типами недосконалої конкуренції.

3. Враховується наявність ресурсних обмежень. При цьому, зви­чайно, розрізняють короткострокові моделі поведінки фірми, коли ресурсні обмеження діють, та довгострокові моделі, коли такі обме­ження практично не беруться до уваги.

4. Метою діяльності фірми є забезпечення максимальних прибутків або мінімізація збитків.

При побудові конкретних моделей поведінки фірми можуть уводи­тись також різні доповнювальні припущення, наприклад, аналіз мо­же вестися із врахуванням фактору часу, не тільки граничних але й середніх величин, більш детально описуватись технологія виробництва тощо.

Розглянемо, як приклад, одну з найпростіших за формою моделей діяльності фірми. При заданій виробничій функції 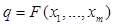заданій ціні на продукцію (умова досконалої конкуренції) та при зада­них цінах на фактори виробництва, що визначають функцію вироб­ничих видатків С(q) від обсягу випуску продукції q, потрібно спря­мувати роботу шляхом вибору q, а значить і вектора витрат виробни­чих факторів 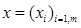, щоб одержати максимальний прибуток 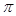, що є різницею між доходом R та видатками С. Будемо вважати, що розглядається довгострокова задача виробництва без обмежень на доступний обсяг виробничих факторів.

Таким чином задача полягає у максимізації функції прибутку :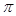

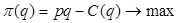(1)

шляхом вибору оптимальної кількості випуску продукції q при умові

q = F(x) (2)

вводячи у розгляд граничні видатки MC(q) [1], M.C(q) = dC(q)/dq, маємо через умову оптимальності випуску 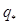першого порядку 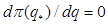, так що для оптимального випуску продукції 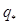ціна по­винна дорівнювати граничним видаткам

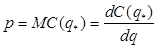(3)

При цьому умови достатності другого порядку для оптимуму 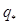ствер­джують. що граничні видатки в точці 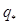повинні зростати

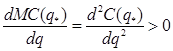(4)

Таким чином оптимальні витрати факторів 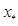в задачі (1)-(2) можна отримати як розв’язок рівняння 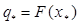де 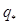визначається умова­ми (3), (4).

Розглянемо випадок, коли 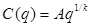, що характерно для однорідних виробничих функцій. Тоді 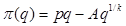. Якщо має місце стала ефекти­вність від збільшення масштабів виробництва (к = 1), то в залежності від значень ціни р та параметру А можливі три таких випадки.

1) р < А. Тоді прибуток від’ємний і фірма має тим більші збитки, чим більший випуск продукції. Тоді оптимальним рішенням є не виробляти про­дукцію (до проведення змін у структурі, технології та діяльності фірми, направлених на покращення її стану), що веде до нульових збитків та при­бутків.

2) р = А. Прибуток дорівнює нулеві незалежно від обсягу випуску про­дукції. Необхідна умова екстремуму виконується у кожній точці.

3) р > А. Прибуток тим більший чим більший обсяг випуску. Необхідна умова екстремуму, як і у випадку р < А, не виконується у жодній точці.

Тобто при обмеженості факторів виробництва задача не має розв’язку. Додаючи обмеження на можливий обсяг випуску через обмеженість факторів виробництва, слід обирати максимальне можливе значення д та, і.

Якщо має місце зростаюча ефективність від збільшення масштабів вироб­ництва (к > 1), то точка, що задовольняє необхідним умовам оптимальності, існує, але це точка мінімуму прибутків, а не максимуму. Прибуток у точці від’ємний. Праворуч від цієї точки чим більший випуск продукції, тим біль­ший прибуток. Задача не має розв’язку, якщо обсяг випуску не обмежений зверху.

Якщо ж має місце спадаюча ефективність від збільшення масштабів виробництва (k < 1), то тільки в цьому разі при всіх значеннях р та А необ­хідні умови оптимальності визначають єдину точку максимуму прибутку. В цьому випадку функція пропозиції, котра співставляє ціні продукції р обсяг випуску q (при фіксованих цінах факторів), виявляється добре визначеною.

Заслуговує на увагу той очевидний факт, що функція пропозиції збігаєть­ся формально із функцією, оберненою до функції витрат. Для однорідної виробничої функції при к < 1 функція пропозиції задається формулою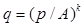

Слід зауважити,, що вибір оптимального обсягу випуску продукції є лиш частиною рішення про планування виробництва. Друга частина рішення полягає у визначенні обсягів витрат факторів виробництва із задачі мінімізації загальних витрат. У дійсності загальне рішення є єдиним рішенням про виробництво продукції та споживання факторів виробництва на основі вихідної інформації про технологію виробництва та ринкові ціни на продукцію і фактори.

Перейдемо тепер до вивчення зв’язків між задачами поведінки фір­ми та результатами сучасного опуклого аналізу, включаючи теорію двоїстості для виробничих функцій. Цікаво, що при цьому рядові формальних понять опуклого аналізу можна дати змістовне економічне тлумачення.

Будемо розглядати довільну угнуту виробничу функцію F: 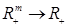(не обов’язково гладку). Припустимо, що ціна вихідної продукції прийнята за одиницю, а ціна на j-тий фактор дорівнює 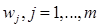т. Розглянемо задачу

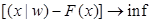
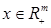(5)

де вектор 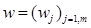є вектором цін факторів виробництва, а 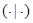позначає скалярний добуток векторів, так що ( 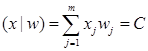є функцією загальних виробничих витрат. Задачу (5) можна інтерпрету­вати як задачу мінімізації збитків виробництва, що дорівнюють 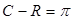бо за умовою R = F(x), (це очевидно еквівалентно задачі максимізації прибутку ).

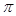Значення задачі (5), тобто значення інфімуму в (5), позначимо через F*(w) і будемо називати функцією спряженою до функції F(x), або функцією збитків.

Зауважимо, що задачу (5) не має смислу розглядати для всіх видів виробничих функцій. Наприклад, для невід’ємних лінійно-однорідних виробничих функцій F, коли 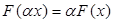для довільних > 0. Справді для таких функцій значення inf в (5) при довільному 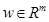не перевищує 0, оскільки 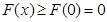F(x) > F(0) = 0. З другого боку, якщо існує 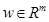, для котрого 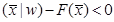, то, очевидно, що на промені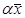 > 0 при 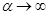а ос величина прямує до 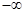. Таким чином для лінійно-однорідних виробничих фун­кцій F функція збитків 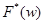у будь-якій точці 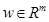приймає значення або 0, або .

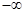Список використаної літератури:
1. Пономаренко, М.О. Перестюк, В.М. Бурим. Основи математичної економіки
2. С.П. Лавренюк. Математичні основи економіки