Краткая теория. Цель работы: определение зависимости прогиба стержня от силы и определение модуля упругости стали, алюминия и латуни.

Лабораторная работа №18

МОДУЛЬ УПРУГОСТИ

Цель работы: определение зависимости прогиба стержня от силы и определение модуля упругости стали, алюминия и латуни.

Приборы и принадлежности: установка для определения модуля упругости, индикатор часового типа, плоские стержни, гири с прорезью.

Краткая теория

Если тело рассматривать как однородное, а 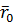или 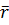определяют вектор P соответственно для малых векторов перемещения в недеформированном и деформированном состоянии:

,

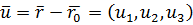то тензор деформации 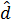равен

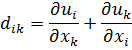
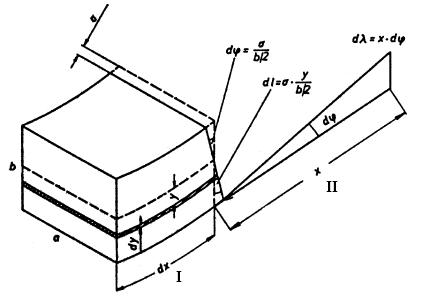
Рис. 3: Деформация стержня.

Силы 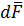, действующие на элементарный объем тела, края которого пересечены параллельно координатным поверхностям, описываются тензором напряжения .

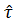Это размещает напряжение 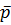по каждому элементарному объему тела 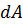определяемое единичным вектором 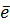по направлению к вектору нормали:

,

.

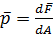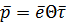Из закона Гука получаем зависимость между 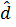и :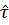

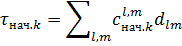
Тензор 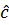симметричен в упругом теле, поэтому из 81 компонента остается только 21. В изотропном теле это число снижается до 2, т.е. модуль упругости E и или модуль сдвига G, или коэффициент Пуассона μ:

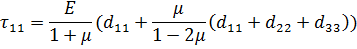
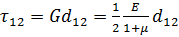(1)

Аналогично для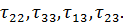

Если сила действует в одном направлении, то

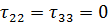
Таким образом, получаем

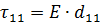(2)

Стержень высотой b и широтой a, имеющий 2 точки опоры на концах на расстоянии L, на который в центре действует сила F_y, ведет себя так же как стержень с точками опоры посередине, на концы которого действует сила F_y /2 в противоположном направлении. Чтобы выразить зависимость прогиба λ от модуля упругости E, сначала следует определить элементарный объем:

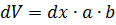
верхний слой которого сокращается при прогибе, а нижний – удлиняется. Длина среднего слоя остается неизменной (нейтральное волокно).

На рис. 3. указателями I и II обозначены стороны до и после деформации.

Учитывая указатели на рис. 3, получаем:

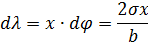
Сила упругости dF_x, вызывающая удлинение dl, согласно выражению (1), составляет

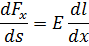
где 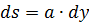‑ площадь повернутого слоя.

Сила вызывает вращающий момент:

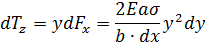
Сумма данных вращающих моментов, вызванных силами упругости, должна равняться моменту, вызванному внешней силой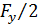

,

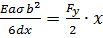из чего получаем

.

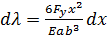Проинтегрировав выражение, получаем общий прогиб:

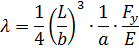
Таблица 1: Модуль упругости различных материалов

Материал	Размеры (мм)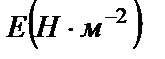
Сталь	10х1, 5	2, 059·1011
Сталь	10х2	2, 063·1011
Сталь	10х3	2, 171·1011
Сталь	15х1, 5	2, 204·1011
Сталь	20х1, 5	2, 111·1011
Алюминий	10х2	6, 702·1011
Латунь	10х2	9, 222·1011

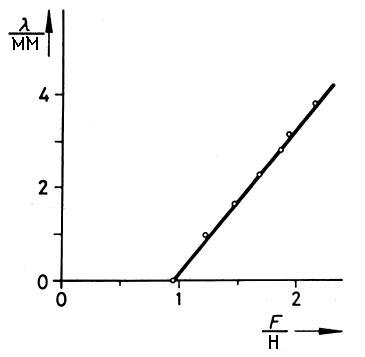
Рис. 4: Зависимость прогиба от силы (материал – сталь, 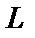= 0, 48 м, 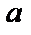= 10 мм, 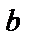= 1, 5 мм).