
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткие сведения из теории. Тема: Исследование арифметического сумматора
|
|
Практическая работа № 7
Тема: Исследование арифметического сумматора
Цель работы – исследовать арифметический сумматор, полусумматор и полный сумматор.
Краткие сведения из теории
Арифметические сумматоры – составная часть арифметико-логических устройств (АЛУ) микропроцессоров (МП). Арифметический сумматор состоит из двух устройств: полусумматора и n полных сумматоров. Полный сумматор имеет три входа: A, B – входы суммируемых операндов, Ci – вход переноса из предыдущего разряда сумматора и два выхода: S – выход полного сумматора и C 0 – выход переноса. Полусумматор отличается от полного тем, что у него нет входа переноса из предыдущего разряда. Полусумматор используется в качестве первого разряда арифметического сумматора, а в качестве остальных разрядов – полные сумматоры (рис. 47). Полусумматор – одна из простейших комбинационных логических схем.
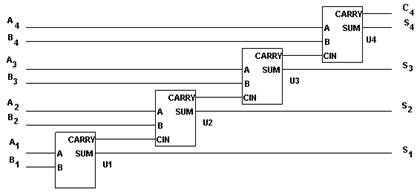
Рис. 47. Четырехразрядный арифметический сумматор
Рассматривая таблицу истинности полусумматора (табл. 12) можно заметить, что выход S полусумматора выполняет функции элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ», а выход переноса С полусумматора – элемента «И». Таким образом, логические выражения для функций S и C равны:
S=AB ′ +A ′ B, C=AB.
Т а б л и ц а 12
| Входы | Выходы | ||
| А | В | S | C |
Схема полусумматора представлена на рис. 48.
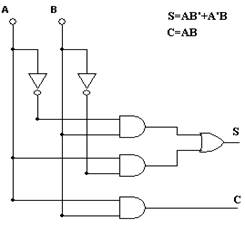
Рис. 48. Структура полусумматора
Из таблицы истинности полного сумматора (табл. 13) можно получить логические выражения для S (суммы) и C (переноса в следующий разряд). Логическое выражение для S будет иметь четыре слагаемых, соответствующих строкам таблицы, в которых выход S равен единице (стоки 4, 5, 7, 10),
S= A ′ B ′ Ci- 1 +A′ BCi- 1′ +AB ′ Ci- 1′ +ABCi- 1.
Т а б л и ц а 13
| Входы | Выходы | |||
| А | В | Ci -1 | S | Ci |
Логическое выражение для C также будет иметь четыре слагаемых (строки 6, 8, 9, 10):
Ci=A ′ BCi- 1 +A ′ BCi- 1′ +ABCi- 1′ +ABCi- 1.
С помощью законов булевой алгебры (см. лаб. раб. №1) это выражение можно упростить, тогда оно будет иметь вид
Сi=ACi- 1 +BCi- 1 +AB.
Схема полного сумматора изображена на рис. 49.
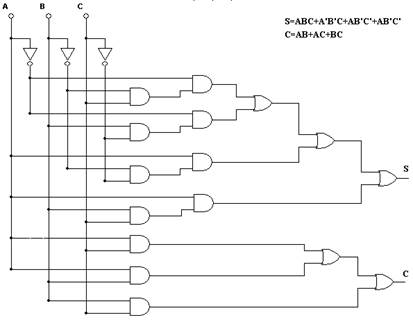
Рис. 49. Структура полного сумматора