
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Выбор как максимизация критерия
|
|
Если теперь сделать еще одно важное предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считать, что выбор осуществляется в условиях определенности) и заданный критерий q(x) численно выражает оценку этих последствий, то наилучшей альтернативой х * является, естественно, та, которая обладает наибольшим значением критерия:
х*= arg max q(x), при условии, что х е X.
Задача определения оптимального решения х*, простая по постановке, часто оказывается сложной для решения, поскольку метод ее решения (да и сама возможность решения) определяется как характером множества X, так и видом критерия. На возможность решения задачи оптимизации критерия оказывает влияние размерность вектора х и тип множества X - является ли оно конечным, счетным или континуальным. В свою очередь критерий может быть сформулирован в виде функции или функционала.
Однако сложность определения наилучшей альтернативы на практике существенно возрастает, так как оценивание любого варианта единственным числом обычно оказывается неприемлемым упрощением. Более полное рассмотрение альтернатив приводит к необходимости оценивать их не по одному, а по нескольким критериям, качественно различающимся между собой. При решении конкретных задач системным аналитикам следует учитывать множество критериев: технических, технологических, экономических, социальных, эргономических и пр.
Итак, пусть для оценивания альтернатив используется несколько критериев qi(х), i = \,..., p. Теоретически можно представить себе случай, когда в множестве X окажется одна альтернатива, обладающая наибольшими значениями всех p критериев; она и является наилучшей. Однако на практике такие случаи почти не встречаются, и возникает вопрос, как же тогда осуществлять выбор.
Путь к единому параметру оптимизации часто лежит через обобщение. Из многих критериальных функций, определяющих альтернативу, трудно выбрать один, самый важный. Будем рассматривать ситуацию, когда необходимо множество критериальных функций свернуть в единый количественный признак. Каждый критерий в общем случае имеет свой физический смысл и свою размерность. Чтобы объединить различные критерии, прежде всего, приходится вводить для каждого из них некоторую безразмерную шкалу. Шкала должна быть однотипной для всех объединяемых критериев - это делает их сравнимыми.
Сведение многокритериальной задачи к однокритериальной
Рассмотрим наиболее употребительные способы решения многокритериальных задач. Первый способ состоит в том, чтобы многокритериальную задачу свести к однокритериальной. Это означает введение суперкритерия, т.е. скалярной функции векторного аргумента:
Ч0(х) = % (?, (*). Я2{х),..., qp(x)).
Суперкритерий позволяет упорядочить альтернативы по величине qo, выделив тем самым наилучшую (в смысле этого критерия). Вид функции qo определяется тем, как мы представляем себе вклад каждого критерия в суперкритерий. Обычно для реализации данной процедуры используют аддитивные
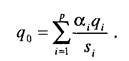
или мультипликативные функции
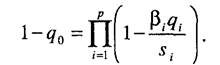
Коэффициенты s. обеспечивают безразмерность критериального значения (частные критерии могут иметь разную размерность, и тогда некоторые арифметические операции над ними, например сложение, не имеют смысла). Коэффициенты а., (3. отражают относительный вклад частных критериев в суперкритерий.
Итак, при данном способе задача сводится к максимизации суперкритерия:
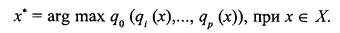
Очевидные достоинства объединения нескольких критериев в один суперкритерий сопровождаются рядом трудностей и недостатков, которые необходимо учитывать при использовании этого метода.
Рассмотрим примеры построения обобщенных критериальных показателей. Пусть рассматриваемая альтернатива характеризуется п частными критериальными функциями qt(i-\, 2,.., p). Каждая из функций q. имеет свой физический смысл и, чаще всего, свою размерность. Введем простейшее преобразование: набор данных для каждого q. поставим в соответствие с самым простым стандартным аналогом -шкалой, на которой имеется только два значения: 0 - брак, неудовлетворительное качество, 1 - годный продукт, удовлетворительное качество. В ситуации, когда каждый преобразованный критерий принимает только два значения 0 и 1, естественно желать, чтобы и обобщенный критерий принимал одно из двух возможных значений, причем так, чтобы значение 1 имело место тогда и только тогда, когда все частные критериальные показатели приняли бы значение равное 1. Если же, хотя бы один из показателей принял значение, равное 0, то и обобщенный критерий будет равным нулю. В этом случае для построения обобщенного критериального показателя естественно воспользоваться формулой
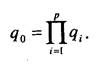
Иногда применяют запись
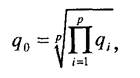
где q - обобщенный критериальный показатель; q. - частные критериальные функции.
Если для каждого из частных критериев известен «идеал», к которому нужно стремиться, то можно предложить следующий метод построения обобщенного параметра оптимизации (критериального показателя). Пусть q.o - наилучшее (идеальное) значение z-го критерия. Тогда (< 7, - Чт) ~ меР^ близости к идеалу. Поскольку при построении обобщенного критериального показателя необходимо, чтобы различные показатели были сопоставимы, надо привести их к безразмерному значению. Это можно осуществить, отнормировав полученное отклонение следующим образом
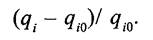
Чтобы исключить влияние знаков, возведем последнее выражение в квадрат
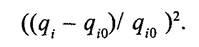
Тогда обобщенный критериальный показатель можно записать
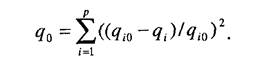
Если все частные критерии совпадают с идеалом, то q0 станет равным нулю. В таком правиле определения обобщенного критериального показателя каждый частный критерий входит в формулу на равных правах. На практике показатели бывают далеко не равноправны. Введем некоторые весовые коэффициенты ос., тогда правило определения обобщенного параметра можно записать в виде:
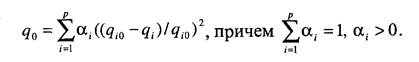
Задача определения значений весовых коэффициентов - это отдельная задача, она не входит в рамки обсуждения.
Если удается построить обобщенный критериальный показатель, то метод поиска оптимального решения будет аналогичен методу оптимизации в случае единственного критерия. В зависимости от вида критериального показателя в качестве метода решения могут быть использованы прямые оптимизационные процедуры, в случае невозможности аналитического решения используются численные методы.
Условная максимизация
Вторым способом решения задач выбора в условиях наличия нескольких критериальных показателей является сведение задачи к задаче условной максимизации. Данный метод решения задач выбора целесообразно применять в тех случаях, когда заведомо известно, что частные критерии неравнозначны между собой, одни из них более важны, чем другие. В этом случае происходит выделение основного, главного критерия, остальные рассматриваются как вспомогательные, дополнительные к выделенному. Такое разделение критериев позволяет сформулировать задачу принятия решений как задачу определения условного экстремума:
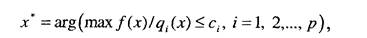
где через/(х) обозначен основной критерий; q.(x) - вспомогательные или второстепенные критериальные функции. В ограничениях могут иметь место различные сочетания знаков: от строгого равенства до строгого неравенства. Например, если вспомогательный критерий характеризует стоимость затрат, то разумнее задавать их верхний уровень и формулировать задачу с ограничениями в виде неравенств. Для решения задач в такой постановке разработаны специальные методы математического программирования, рассмотренные в гл. 2 работы [57].
Нахождение паретовского множества
Следующий способ многокритериального выбора состоит в сравнении альтернатив между собой по всем сформированным критериям и выделении подмножества наилучших альтернатив. В данном подходе отказываются от поиска одной единственной наилучшей альтернативы. Решающее правило в этом случае строится на основе аксиомы В. Парето, которая формулируется следующим образом: «Если в задаче принятия решений частные критерии независимы по предпочтению и значение каждого из них желательно увеличивать, то из двух альтернатив, характеризуемых набором частных критериев, предпочтительнее та, для которой выполняются соотношения qu(x) > q2i(x) по всем i, где первый индекс характеризует номер стратегии, второй индекс -номер частного критерия. То есть первая альтернатива предпочтительнее второй только в том случае, когда значения ее частных критериев не меньше значений частных критериев второй альтернативы. Если все значения частных критериев одной альтернативы равны значениям критериев другой, то альтернативы равнозначны». Таким образом, предпочтение одной альтернативе перед другой можно отдавать только если первая по всем критериям лучше второй. Если же предпочтение хотя бы по одному критерию расходится с предпочтением по другому, то такие альтернативы признаются несравнимыми. В результате попарного сравнения альтернатив все худшие по всем критериям альтернативы отбрасываются, а все оставшиеся несравнимые между собой принимаются. Если все максимально достижимые значения частных критериев не относятся к одной и той же альтернативе, то принятые альтернативы образуют множество Парето и выбор на этом заканчивается. При необходимости выбора единственной альтернативы следует привлекать дополнительные соображения: либо корректировать систему предпочтений, либо обращаться к услугам экспертов, либо воспользоваться методами, рассмотренными ранее (построение обобщенного критерия или сведение задачи к задаче поиска условного экстремума).
13.3. Выбор в условиях неопределенности
Рассмотренные до настоящего времени задачи осуществления выбора формулировались таким образом, что последствия сделанного выбора предполагались однозначно определенными. Выбор одной из альтернатив был связан с известным однозначным следствием. В этом случае проблема выбора состояла в сравнении разных вариантов, т.е. альтернатив.
В реальной практике в большинстве случаев приходится иметь дело с более сложной ситуацией, когда выбор альтернативы неоднозначно определяет последствия сделанного выбора. Адекватное реальности описание проблемы практически всегда содержит различного рода неопределенности, отражающие то естественное положение, в котором находится исследователь: любое его знание относительно и неточно. Принято различать три типа неопределенностей. С одной стороны это неопределенности природы. К данному виду неопределенностей относят факторы, неизвестные исследователю. Далее неопределенности противника. Нередки ситуации, когда исследователь принимает решения в условиях, при которых результаты его решений не строго однозначны. Они зависят от действий других лиц (партнеров, противников и т.п.), которые он не может учесть или предсказать. И, наконец, существуют так называемые неопределенности целей. Такая ситуация возникает в случае, когда при принятии решений формулируется несколько целей, которые в общем случае могут противоречить друг другу. В этом случае мы приходим к многокритериальной задаче выбора. Подходы к принятию решения в условиях многокритериальной задачи рассмотрены в предыдущем параграфе.
Существует также классификация неопределенностей по соотношению альтернатив и исходов. Различают неопределенности дискретного и непрерывного типа, стохастические и расплывчатые неопределенности.
Рассмотрим следующую ситуацию: имеется набор возможных исходов у е Y, из которых один окажется совмещенным с выбранной альтернативой, но какой именно - в момент выбора неизвестно, а станет ясным позже, когда выбор уже сделан и изменить ничего нельзя. Будем предполагать, что с каждой альтернативой х связано одно и то же множество исходов Y, для разных альтернатив одинаковые исходы имеют разное значение. В случае дискретного набора альтернатив и исходов такую ситуацию можно изобразить с помощью матрицы, представленной в табл. 13.1:
Таблица 13.1
| У\ | У) | У- | |||
| Х\ | <? " | Чч | Ч\т | ||
| Xi | *i | Чч | Qim | ||
| х„ | Чч | Чгт |
В этой матрице все возможные исходы образуют вектору = (у,,..., ут), числа q.. выражают оценку ситуации, когда сделан выбор альтернативы х.п реализовался исходу.. В конкретных случаях числа q.. могут иметь различный смысл: это может быть «выигрыш», «потери», «платежи» и т.п. Если все строки q. = (qn,..., qjm) при любых г одинаковы, то проблемы выбора нет. Если же строки матрицы различны, возникает вопрос, какую альтернативу предпочесть, не зная заранее, какой из исходов реализуется.
Аналогичная ситуация возникает в случае, когда множества X и Y непрерывны. В этом случае зависимость между альтернативами и исходами задается в виде функции q(x, y), x e X, y e Yc соответствующей постановкой вопроса о выборе х.
Введенных до настоящего времени параметров недостаточно для формальной постановки задачи выбора. При различной конкретизации этой задачи она приобретает различный смысл и требует различных методов решения. Методологической базой для решения такого рода задач является теория игр. Метод решения конкретной задачи будет зависеть от характера воздействующих на ситуацию факторов, не зависящих от лица, принимающего решения. Здесь необходимо различать уже отмеченные ранее неопределенности природы и неопределенности противника. В задачах выбора с природной неопределенностью считается, что исходы у = (ур..., ут) есть возможные состояния природы. Желательность каждой альтернативы х, зависит от того, каково состояние природы, но узнать это состояние исследователь сможет лишь после того, как сделан выбор.
В задачах выбора с неопределенностью противника предполагается, что исходы Y- это множество альтернатив, на котором выбор осуществляет второй игрок. В отличие от природной неопределенности игрок преследует свои интересы, отличные от интересов исследователя (первого игрока). При этом матрица Q = Ц^Ц, характеризующая оценки ситуаций с точки зрения системного исследователя или лица, принимающего решения, выбирающего х, уже недостаточна для описания всей ситуации. Необходимо задать вторую матрицу и = ||м; ,.|, описывающую систему предпочтений с позиции противника. Задание X, Y, < 2 и [/называется нормальной формой игры. Расхождение между матрицами Q и U определяет степень антагонизма лица, принимающего решения, и его противника. Остановимся на анализе природных неопределенностей и неопределенностей противника.
Природные неопределенности
Рассмотрение природных неопределенностей начнем с примера. Пусть перед системным аналитиком стоит задача проложить маршрут океанского лайнера и распорядиться запасом горючего так, чтобы судно как можно быстрее дошло до пункта назначения. При этом известно, что время нахождения в пути будет существенно зависеть от погодных условий на трассе в момент ее прохождения. В данном случае погодные условия представляют собой природную неопределенность. Ситуация типична для ряда задач принятия решений. Рассмотрим ее формализацию. Запишем целевую функцию, например время нахождения судна в пути, в следующем виде
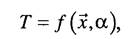
где а е Ga - некоторый параметр, который заранее неизвестен. Выбор альтернативы х, которая бы минимизировала значение целевой функции будет существенно зависеть от того, какое значение параметра а реализуется в момент прохождения судна по трассе. Таким образом, говоря о природной неопределенности, имеем в виду, что выбор осуществляется в условиях, когда целевая функция задана, но не совсем точно, а именно, она содержит неопределенный параметр. Постановка задачи выбора будет выглядеть следующим образом
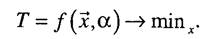
При этом решение будет представлять собой функцию от параметра а: х =х(ос). Если никакой дополнительной информацией о факторе неопределенности ос лицо, принимающее решение, не располагает, то результат оптимизации произволен. В реальных ситуациях информация о параметре ос обычно имеет вид ос е G, где G - некоторое множество. Но подобной информации также недостаточно для однозначного решения задачи. Решение х = х(ос) определяет лишь некоторое отображение множества неопределенности природных факторов Ga на множество альтернатив X, которое естественно назвать множеством неопределенности результата. Множество неопределенности результатах- важная характеристика процедуры принятия решений, но его построение сопряжено с большим объемом сложных вычислений.
Рассмотрим другой подход, который дает строгую оценку. Данный подход основан на применении принципа наилучшего гарантированного результата. Суть его состоит в следующем. Так как для любой альтернативы х справедливо неравенство
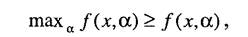
Число f *, определенное данным способом, называется гарантированной оценкой, а соответствующая альтернатива х - х* - гарантированной стратегией в том смысле, что каково бы ни было значение параметра неопределенности ос, выбор х = х* гарантирует, что при любом а значение целевой функции будет не меньше, чем f*.
Выбор гарантирующей стратегии поведения - это рациональный способ принятия решений. В результате использования данной стратегии лицо, принимающее решение, гарантирует исход, защищенный от всевозможных случайностей. Каковы бы ни были неконтролируемые факторы, в результате такого выбора обеспечивается значение целевой функции не меньше, чем/*. Данный результат может быть улучшен, если принять решение, связанное с определенным риском. Критерии принятия решений в условиях риска рассмотрим несколько позже.
Неопределенности противника
Перейдем теперь к описанию неопределенностей, связанных с существованием активных партнеров или противников, действия которых лицо, принимающее решение, не может полностью контролировать.
В теории принятия решений особое место занимает изучение ситуации, в которой участвует много субъектов (много оперирующих сторон), причем каждый из них стремится достичь своей цели
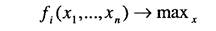
и имеет для этого определенные возможности, которые описываются вектором х, х е X. Заметим, что формально такая ситуация включает в себя проблему многокритериальности, требующую определения вектора х, при котором достигается максимум критериев ffX). В самом деле, если отождествить цель каждого из субъектов с его критерием ДХ), а в качестве описания множествах принять условия
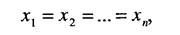
то в результате будет получен частный случай задачи со многими активными партнерами. Общий случай ситуации со многими субъектами гораздо сложнее и требует для своего анализа целый ряд специфических гипотез. Поясним это на примере двух субъектов. Итак, пусть два субъекта Aw. Б, располагающие возможностью выбора векторов х и у, стремятся к достижению своих целей, которые будем записывать в виде
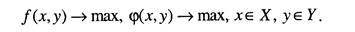
В частном случае может оказаться, что/(х, у) - - ф(х, у); такую ситуацию называют антагонистической. Антагонистические ситуации были предметом множества исследований и сделались основным объектом изучения в теории игр. Чисто антагонистическая ситуация является в известном смысле вырожденной. Наиболее типичен конфликт, в котором интересы партнеров или противников не совпадают, но и не строго противоположны.
Общий случай нетождественности интересов (целей) партнеров (субъектов) называют конфликтом. При изучении конфликтных ситуаций, т.е. при изучении возможных способов выбора, удобно отождествлять исследователя с одним из субъектов. Условимся называть лицо, принимающее решение субъектом А.
В связи с тем, что исход выбора зависит от выбора субъекта Б, необходимо принять ту или иную гипотезу о его поведении, которое, в свою очередь, будет зависеть от характера информированности субъекта Б. Здесь возможно существование нескольких гипотез (нескольких • случаев).
1) Каждый из субъектов не имеет никакой информации о выборе, который сделал другой субъект. В этом случае имеется возможность найти гарантированную оценку. Для субъекта А она будет выражаться формулой
f=maxxminyf(x, y), для субъекта Б - формулой
ф* = max min x ф(х, у).
Решая сформулированные задачи, определяют векторы х* и у*, которые реализуют значения/* и ф*. Такое решение означает, что сделав выбор х = х*, лицо, принимающее решение, при любых условиях (любом выборе у е У) гарантирует, что значение целевой функции/(х, у) будет не меньше, чем/*.
В этой ситуации могут быть предложены различные варианты риска. Например, имеется возможность принять гипотезу о том, что другой субъект использует гарантирующую стратегию у = у*. Тогда необходимо делать другой выбор:
/* =ma.xxf(x, y').
В этом случае определяется вектор х = х1 и соответствующее значение функции/=/'. При этом/1 > /, но если противник сделает иной выбор, например, у - у\ то может оказаться, что/(х', у1) < /*. В данной ситуации следует иметь в виду, что риск есть риск, и если исследователь сформулировал гипотезу и она оказалась неверной, то и результат может оказаться не тем, который ожидается.
2) Вторая ситуация характеризуется тем, что исследователь во время принятия решения имеет информацию о выборе субъекта Б, т.е. ему известно выбранное субъектом Б значение у.
Тогда стратегию (выбор) х следует искать в виде функции х = х(у). Данная стратегия может быть определена эффективно, для этого требуется решить задачу оптимизации
f(2) =тзх xf(x, y).
Решая данную оптимизационную задачу, определяем искомую стратегию х = х(у). Для этого случая можно также вычислить гарантированный результат (он будет отличен от/*):
/ =minmaxxf(x, y)
и во всех случаях / > / *.
Заметим, что выбирая свою стратегию - вектор х - лицо, принимающее решение, никак не можем повлиять на выбор, который сделал другой субъект.
3) Предположим теперь, что субъект Б в момент принятия своего решения будет знать выбор лица, принимающего решение (субъектаЛ); например, субъект Л обязан сообщить свое решение субъекту Б. В этом случае исключается возможность оказать влияние на выбор, который сделает субъект Б. В самом деле, если исследователь знает целевую функцию субъекта Б, то естественно сделать предположение о том, что субъект Б будет делать выбор из условия
ф = тахуф(.х,; у).
Решая данную задачу исследователь может определить отклик субъекта Б на свой выбор, который, согласно сформулированной гипотезе, будет оптимальной стратегией субъекта Б:
У = У(х)-
Теперь имеется возможность распорядиться выбором вектора х. Подставляя последнее выражение в формулу для целевой функцииДх, у), можно получить
f(x, y(x)) = F(x).
Свой выбор исследователь может сделать из условия
/< 3> = F(x).
Итак, информация о том, что субъект Б будет знать выбор лица, принимающего решения, а также гипотеза о том, что субъект Б выберет свою оптимальную стратегию, позволяют так воздействовать на его выбор, чтобы он в максимальной степени соответствовал целям исследователя.
Описанная ситуация достаточно часто встречается на практике и ей нетрудно придать ту или иную экономическую интерпретацию. Так, вектор х можно отождествить с ресурсом, а функцию у = у(х) назвать производственной функцией, которая описывает наивыгоднейший для субъекта Б способ использования ресурса. Таким образом, субъекту Б выделяется такое количество ресурса, чтобы его деятельность наилучшим образом соответствовала целям субъекта А.
Критерии сравнения альтернатив
Теория принятия решений в настоящее время представляет собой самостоятельную научную дисциплину. По данному направлению опубликовано множество монографий [3], поэтому не имеет смысла подробно останавливаться на результатах данной теории. Изложим основополагающие идеи и подходы к решению задач теории принятия решений.
Центральным моментом данной теории является введение критерия для оценки выбираемого варианта. В силу неопределенности исхода требуется дать оценку сразу целой строке матрицы (см. табл. 13.1). Имея такие оценки для всех строк, и сравнивая их, можно приступать к решению задачи выбора. Для этого требуется ввести критерии сравнения альтернатив.
Самым распространенным является уже рассмотренный ранее максиминный критерий, который гарантирует результат выбора по принципу «наименьшего из зол». Рассмотрим суть данного критерия применительно к табл. 13.1 (матрица платежей). В каждой из строк матрицы определяем наименьший из выигрышей minjqij, который характеризует гарантированный выигрыш в самом худшем случае. Данное значение считаем оценкой альтернативы х.. Далее определяем альтернативу х'', обеспечивающую наибольшее значение этой оценки:
х* = are max. min. a...
Эта альтернатива называется оптимальной по максиминному критерию. Если платежную матрицу определить не через выигрыш, а через проигрыш, то тот же принцип рассмотрения приводит к минимаксному критерию. Минимаксный критерий использует оценочную функцию, соответствующую позиции крайней осторожности. Правило выбора решения в соответствии с минимаксным критерием можно интерпретировать следующим образом: матрица платежей, на основании которой осуществляется поиск оптимального решения, дополняется еще одним столбцом из наименьших результатов q.r каждой строки. Выбрать надлежит те варианты х., в строках которых стоят наибольшие значения q.r этого столбца.
Выбранные таким образом варианты полностью исключают риск. Это означает, что лицо, принимающее решение, не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Какие бы условия ни сложились при развитии ситуации, соответствующий результат не может оказаться ниже q. Это свойство заставляет считать минимаксный критерий одним из фундаментальных. В задачах системных исследований применительно к техническим системам данный критерий находит наиболее широкое применение. Однако следует заметить, что положение об отсутствии риска стоит различных потерь. Осознавая данную ситуацию, в теории принятия решений предложено большое количество критериев, учитывающих всевозможные особенности конкретных задач и предпочтений субъектов, принимающих решения. Это такие критерии как Байеса-Лапласа, Сэвиджа, Гурвица, Ходжа-Лемана, Гермейера и т.д. Детальное описание данных критериев можно найти, например, в [3].
Применение минимаксного критерия бывает оправдано в ситуациях, которые характеризуются следующими обстоятельствами:
• о возможности появления внешних состояний ничего не известно;
• приходится считаться с возможностью появления нескольких различных по своему характеру негативных внешних состояний;
• решение реализуется лишь один раз;
• при принятии решения необходимо исключить любой риск, т.е. ни при каких условиях не допускается получать результат, меньший чем
13.4. Концепция риска в задачах системного анализа
Допущение пусть даже малой вероятности а принятия ошибочного решения не исключает возможности риска. Полное устранение риска при принятии решений практически даже и не требуется; мало того, определенная степень риска вводится сознательно, так как принятие решения без риска, например, с предельно пессимистической позиции, как правило, невыгодно. Однако при этом разумный риск следует отличать от риска азартного игрока. Любой риск, во-первых, должен учитываться по возможности полно, описываться количественными характеристиками и ограничиваться, а во-вторых, ни в коем случае не превышать уровень, при котором результат достигается с достаточной надежностью. В качестве опорного для оценки риска принимается решение, получаемое на основании минимаксного критерия, так как данное решение соответствует позиции крайней осторожности.
В литературе встречается различное понимание термина «риск» и в него иногда вкладывают довольно сильно отличающиеся друг от друга трактовки. Однако общим во всех этих представлениях является то, что под риском понимают неуверенность, произойдет ли нежелательное событие и возникнет ли неблагоприятное состояние. Проблемы риска, тем не менее, часто приходится решать, и выбор варианта решения в общем случае, так или иначе, связан с риском. Поэтому попытаемся найти такое определение риска, которое в достаточной степени соответствовало бы содержанию рассматриваемых задач и в то же время отвечало бы общей концепции теории принятия решений.
С понятием риска часто связывается представление о возможных или грозящих событиях с катастрофическими последствиями и потерями. Отсюда следует точка зрения, что такого события следует избежать любой ценой. При ожидаемых потерях, связанных с жизнью и здоровьем, это представление выражено особенно резко, и оно ясно формулируется в соответствующих инструкциях, например по технике безопасности. Конечно, нужно четко сказать, что полностью свободной от риска техники, несмотря на самые большие затраты, не существует. Однако техническим задачам далеко не всегда сопутствуют такие отягчающие обстоятельства. Ущерб вследствие решения, принятого с учетом риска, может оказаться ничтожно малым по сравнению с затратами на то, чтобы избежать такого ущерба. Учитывая необходимость количественных оценок, можно предложить следующую формулировку понятия риска: величина риска, связанная с реализацией нежелательного события или состояния, есть произведение величины последствий реализации события на меру возможности его наступления.
Обозначим через А некоторое нежелательное событие или состояние, которое может произойти. Пусть данное событие характеризуется некоторой вероятностью наступления Р(А) и некоторыми последствиями U(A). Тогда риск, связанный с наступлением события Л, будет определяться следующим образом:
R(A) = ЩА) Р(А).
Последствие в принципе нежелательного события или состояния может в соответствии со своей величиной описываться и оцениваться специфическими параметрами. Диапазон при этом весьма широк - от экономических до этических ценностей. Мерой возможности наступления события служит вероятность q его наступления.
При угрозе материальным ценностям степень риска измеряют в денежном выражении. Если различные последствия нежелательного
события одинаковы или очень велики, то для сравнения достаточно рассматривать одни соответствующие вероятности. Наряду с этим может быть угроза ценностям, которую нельзя выразить количественно, например, когда последствия события нельзя предусмотреть достаточно полно. Примером могут служить последствия выхода из строя прибора, используемого в различных областях народного хозяйства, которые поставщик оценить не может. В этом случае мерой риска остается принять вероятность превышения предела нагрузки. При риске, связанном со здоровьем, последствия могут быть частично оценены количественно в таких категориях, как простой в работе или расходы на оплату подменяющего персонала и т.п. При риске, связанном с летальным исходом, количественные оценки последствий в большинстве случаев отсутствуют. При существовании угрозы жизни люди в настоящее время почти всегда, тем не менее, работают. Особые проблемы возникают в случаях, когда опасность грозит и людям, и материальным ценностям одновременно, и желательно меру такого риска сравнить с другими рисками. Риск может быть явно связан с факторами, не поддающимися учету. Так, эстетический вред, наносимый построенным сооружением уникальному ландшафту, практически невозможно оценить.
Заключительная оценка риска бывает проста, когда имеют дело только с угрозой материальным ценностям, а возможный ущерб выражен количественно. При угрозе материальным ценностям и невозможности количественно выразить возможный ущерб нужно этот ущерб оценить приблизительно и продолжать рассмотрение, мирясь с таким недостатком информации. Поскольку нецелесообразно идти на сколь угодно большие затраты, чтобы устранить риск полностью, нужно оценить угрозу людям. Субъективные оценки сильно отклоняются от известных частот реализации тех или иных нежелательных событий. Значения риска субъективно привлекательной деятельности обычно занижаются. Риск события, на которое оценивающему трудно или невозможно оказать влияние, наоборот, обычно переоценивается. Риск события катастрофического характера, как правило, тоже получает более высокую оценку. Кроме того, субъективные оценки меняются со временем. В результате из-за этих некорректностей субъективные оценки не могут быть положены в основу технических решений.
Сравнение рассматриваемой рискованной ситуации с возникавшими в прошлом аналогичными ситуациями дает для оценки риска более надежные исходные данные. Проблема оценки этим, однако, все же не решается. В отдельных случаях, конечно, можно довольствоваться требованием, чтобы допустимый риск был заведомо ниже имевшего место в аналогичных ситуациях ранее. Но в других случаях, особенно при очень высоком уровне затрат, проблема остается нерешенной. Требование четко ограничить допустимые вероятности реализации нежелательного события наталкивается на препятствия, обусловленные следующими положениями:
• такого рода границы должны быть независимыми от экономических затрат, но аналогичная независимость должна существовать также для угрозы безопасности людей и материальным ценностям;
• лицо, принимающее решения, должно для подобных границ принимать общее решение, учитывающее всю специфику частных случаев;
• одно лишь утверждение, что такие границы будут соблюдаться, может освободить лицо, принимающее решение, от обязанности анализировать ситуацию дальше и направлять свои усилия на дальнейшее снижение угрозы безопасности людей. При этом возможны случаи, когда ценой очень небольших затрат опасность может быть еще больше снижена, а этим пренебрегают, поскольку границы уже установлены;
• утверждение, что выдерживаются определенные границы, предполагает качественное единство данных, что на самом деле недостижимо, так как имеют место проблемы самого различного типа;
• ограничения допустимого риска зависят от времени и меняются с изменениями технических и экономических возможностей общества.
Угроза безопасности людей чаще всего состоит из многих составляющих риска, например, из основного существующего риска, риска вследствие ошибок и риска, на который идут сознательно при известных условиях.
Любой математический алгоритм оценки риска должен исходить из того, что твердо установлен экономический эквивалент угрозы. Этот эквивалент должен быть обоснован в том смысле, что он соответствует затратам, которые общество при данных условиях может себе позволить, чтобы предотвратить или уменьшить угрозу. Необходимо воспрепятствовать тому, чтобы, с одной стороны, ценой больших затрат был уменьшен и без того незначительный риск, а с другой - чтобы оставался большой риск, который может быть устранен с небольшими затратами. Установить такой эквивалент - еще не значит добиться успеха. И при многоцелевых решениях эквивалент такого типа не удается получить без влияния субъективных факторов. Тем не менее, эти эквиваленты делают более ясным риск при принятии решения и помогают лучше определить ответственность за выполненную оценку. Решения, связанные с риском, всегда остаются для исследователя сомнительными, так как нельзя заранее определить затраты для четкого разделения во всех случаях оправданного и неоправданного риска. Проконтролировать, был ли оправдан данный риск, удается всегда только после наступления нежелательного события, и возможно это только при оправданных убытках.
Примеры формирования риска в задачах системных исследований
Технический риск. Технические объекты подвергаются опасности при возрастании нагрузки. Если при этом будет превзойден предел (например, прочности), произойдет выход объекта из строя. В данном частном случае под риском целесообразно понимать вероятность наступления определенного сочетания неблагоприятных событий. Риск целесообразно описывать вероятностью при следующих условиях:
а) если последствия выхода из строя объекта нельзя выразить экономическими показателями;
б) если экономические соображения играют подчиненную роль;
в) если экономические последствия важны, но не поддаются количественной оценке;
г) если последствия столь велики, что без особых рассуждений нужно минимизировать вероятность выхода объекта из строя.
Технический риск характеризуется, таким образом, вероятностью превышения предела. Если X и 7- случайные переменные, причем X характеризует нагрузку, a 7- несущую способность, то для технического риска справедливо соотношение
Rm=p{X> Y).
Если существуют плотности распределения нагрузки и несущей способности fjx) и/у(у), то при независимости X и 7 можно записать
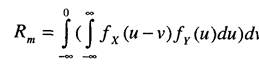
Если, кроме того, известна зависимость плотностей распределения от временных, t) ufy(y, t), то получим
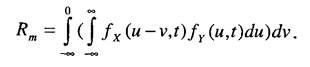
Зависимость плотности распределения нагрузки от времени отражает характер воздействия факторов во времени на исследуемый объект. Зависимость плотности распределения несущей способности от времени отражает процессы старения в самом исследуемом объекте.
Таким образом, задача определения технического риска сводится к определению плотностей распределения нагрузки и несущей способности.
Технико-экономический риск. В данном пункте рассмотрим случай, когда последствия при конкретных нагрузке X и несущей способности Y можно описать функцией h(x, у). На первый взгляд кажется важным рассмотреть критический случай, когда х > у, т.е. когда уровень нагрузки превышает несущую способность. Это условие можно было бы выразить в виде h(x, у) = 0 для х < у и однозначно оценить критический случай х> у простым утверждением, что при этом h(x, y) = \. Однако реальные данные из практики показывают, что первые признаки разрушения появляются еще до достижения нагрузкой несущей способности, и, наоборот, в других случаях, при нагрузке, превышающей несущую способность, объект продолжает функционировать. Так что ограничение функции h(x, у) всего двумя значениями 0 и 1 может оказаться слишком грубым описанием. Определим технико-экономический риск Re при независимости нагрузки X и несущей способности Уи известных ^плотностях распределения fjx) и/у(у) ожидаемых случайных величин следующим соотношением:
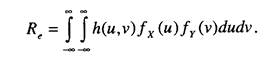
Для определенного данного значения х нагрузки условное математическое ожидание риска равно
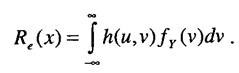
Угроза безопасности людей. Если при анализе безопасности технических объектов существуют события А., при достижении которых возникает угроза здоровью обслуживающего персонала, описываемая количественно функцией потерь h(A), то для описания функции риска можно пользоваться выражениями, аналогичными тем, которые были получены для технико-экономического риска. Если функцию потерь сформировать не удается, то в качестве меры риска допустимо использовать вероятность наступления нежелательного события, как это было сделано в случае технического риска. Дополнительно следует, однако, рассмотреть еще ряд возможных случаев.
Угроза при эксплуатации технических средств определяется двумя категориями влияний - событиями, представляющими угрозу, и попаданием в опасную зону. События, представляющие угрозу, и попадание в опасную зону - явления случайные. В предположении равномерности распределения событий во времени можно получить следующие выражения для вероятности наступления события, представляющего угрозу:
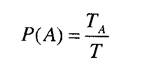
и для вероятности попадания в опасную зону:
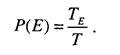
То есть вероятности выражаются как отношения интервалов времени. Здесь приняты следующие обозначения: ТА - суммарная продолжительность события, представляющего угрозу; ТЕ - продолжительность пребывания в опасной зоне; Т - рассматриваемый интервал времени, для которого принимается решение.
Если событие А, представляющее угрозу, и пребывание в опасной зоне Е независимы, то вероятность совместной реализации этих двух событий можно оценить по формуле
Р(АпЕ) = Р(А)Р(Е).
Эта формула говорит, что при данных значениях Р(А) и Р{Е) следует считаться с вероятностью совпадения опасностей, т.е. одновременного наступления представляющего угрозу события и попадания в опасную зону в рассматриваемый отрезок времени. Однако отсюда не следует, с какой вероятностью нужно ожидать реализации по меньшей мере одной угрозы. Поэтому при использовании величины как вероятности угрозы возможны серьезные ошибки в интерпретации рассматриваемых ситуаций.
13.5. Принятие решений в условиях стохастической неопределенности
При решении вопросов системных исследований, таких как проектирование автоматизированных систем, организация их эксплуатации и т.п. возникает большое количество задач, в основе которых лежат вероятностные модели объектов или процессов, описывающих исследуемые явления. Примерами таких задач являются задачи оценивания параметров эффективности и надежности технических средств, прогнозирование поведения параметров системы, задачи, связанные с контролем работоспособности и диагностикой неисправностей при функционировании систем и отдельных компонентов, задачи организации оптимального обслуживания технических средств, задачи обоснования срока службы отдельных элементов, узлов, подсистем. В большинстве случаев существуют естественные вероятностные модели, отражающие реальный ход процессов динамического поведения объектов. Эти модели строятся на основе математических, физических или технических закономерностей, отражающих функционирование отдельных объектов, воздействие объектов друг на друга. В ряде случаев для построения вероятностной модели используется объективная информация о поведении объектов в процессе эксплуатации. По результатам обработки этой информации с помощью специальных методов математической статистики производят построение зависимостей. Например, существующие методы проверки статистических гипотез позволяют обоснованно подойти к выбору закона распределения некоторой случайной величины на основании реализовавшихся значений.
И, наконец, существуют ситуации, когда построение вероятностной модели происходит субъективно, на основании интуиции и опыта системного аналитика. При построении вероятностной модели на основании субъективной информации необходимо тщательно анализировать комбинации состояний динамических объектов, возможность появления критических ситуаций, степень вероятности ситуаций. Необходимо также привлекать информацию о сходных процессах, результатах приближенных расчетов.
Следует заметить, что при построении вероятностных моделей процессов предпочтение следует отдавать моделям, учитывающим объективные данные. Субъективные оценки необходимо применять, когда отсутствуют возможности для получения объективных данных. Однако в некоторых задачах учет субъективных вероятностей наряду с объективной информацией бывает весьма полезным. При формировании субъективных вероятностей исследователь должен постараться выразить вероятности рассматриваемых событий через вероятности более простых явлений, которые либо являются заданными, либо поддаются объективной оценке или вычислению.
Общей чертой всех подобных задач является необходимость выбора на основании косвенных или прямых, но обязательно «зашумленных» данных. Основным предположением для формализации решения задач такого типа является предположение о вероятностном характере экспериментальных данных.
Методологической основой для решения задач выбора в такой постановке является теория оптимальных статистических решений. В основе данной теории лежит понятие статистической функции риска.
Рассмотрим постановку задачи. Будем считать заданным вероятностное распределение Р на множестве возможных исходов Y, причем значение Р(у) определено для каждого исхода у. Предположим, что системный аналитик, не зная результата развития системы, должен принять решение, последствия которого зависят от этого результата (исхода). Пусть X множество всех возможных решений, которые может принять исследователь. Положим, что в результате выбора решения х и реализации исхода у исследователь получает доход г, принадлежащий пространству всех возможных доходов R. Понятие «доход» обычно определяют через полезность, которая служит для численного выражения предпочтений лица, принимающего решения.
Элементы множества R, которые названы доходами, могут быть весьма сложными объектами. Приведем примеры: множество билетов на различные концерты; множество возможных экономических состояний фирмы в определенный момент времени в будущем, измеряемых разностью ее денежных доходов в будущем и в настоящий момент; множество экономических состояний государства и т.д.
Рассмотрим пример, иллюстрирующий понятие дохода в задачах системных исследований. Пусть решается задача выбора варианта реализации структуры сложной системы. Группа проектировщиков должна принять решение о выборе одного варианта реализации системы управления из нескольких рассматриваемых. В качестве множества доходов, получаемых от реализации того или иного варианта, могут служить денежные доходы, получаемые в результате внедрения системы выработки и принятия управляющих воздействий с использованием конкретного варианта структуры системы по сравнению с традиционным способом управления. Под доходом может также пониматься длительность обработки запросов пользователей; длительность обработки результатов функционирования отдельных подразделений, например цехов; точность и достоверность выводов, полученных в результате реализации управляющих воздействий и т.д. Совокупность всех этих составляющих образует вектор дохода конкретного варианта реализации структуры системы.
Для любого множества R у системного аналитика будут предпочтения к тем или иным доходам. В некоторых ситуациях эти предпочтения очевидны. Например, в случае денежных доходов, чем больше доход, тем он предпочтительнее.
Сложнее сформулировать предпочтение в случае, когда доход -векторная величина. При сравнении двух векторных доходов, если каждая компонента первого вектора представляется более желательной, нежели соответствующая компонента второго вектора, то предпочтение отдается первому вектору. Если первый выгоднее только в отношении некоторых своих компонент, в то время как второй вектор предпочтительнее по другим компонентам, то какому из этих векторов отдать предпочтение, не очевидно. Для окончательного решения вопроса следовало бы приписать соответствующие веса отдельным компонентам.
При сравнении двух доходов г, е R и r2 e R пишут гу< гг, если г2 предпочтительнее rv и г, = г2, если гх эквивалентен г2, т.е. имеет место одинаковая выгодность. Если гх не является более предпочтительным, чем rv то пишут г, < г,.
Предполагается, что на основе своих предпочтений среди доходов системный аналитик может задать полное упорядочение множества R. Другими словами налагаются следующие условия.
1. Если г, и г2 - произвольные доходы из множества R, то верно одно и только одно из следующих соотношений:
2. Если г,, г2 и гъ - доходы из R, причем г, < г2 и г, < гъ, то г{ < гу Наконец, будем предполагать, что не все доходы в R эквивалентны
между собой, т.е. исключается тривиальная ситуация, а именно, предполагается, что s0 -< t0 хотя бы для одной пары s0 e R, tQe R.
В большинстве задач аналитик не вполне свободен в выборе дохода. Обычно он может лишь выбрать из некоторого класса возможных распределений вероятностное распределение на R, согласно которому будет определен его доход.
Например, ставится вопрос о выборе определенного технологического процесса из двух или более возможных таких процессов. Хотя доходы и можно точно выразить через производительность и издержки, производственные характеристики различных процессов могут быть описаны лишь вероятностью.
Другой пример. Системный аналитик хочет получить информацию о значении некоторого параметра. Его доход - это количество информации об этом значении, получаемое после эксперимента. Пусть он выбирает эксперимент из некоторого класса доступных ему, но информация, которую он получит в каждом из экспериментов, носит случайный характер. В любой задаче такого рода аналитик производит выбор не непосредственно среди доходов из множества R, а среди вероятностных распределений на R.
Вероятностное распределение на множестве доходов задают в том случае, когда величина, определяющая доход, имеет характер непрерывной случайной величины. Так, в задаче выбора определенного технологического процесса из нескольких возможных вариантов для каж-
дого процесса могут быть известны средние характеристики. Однако в реальной эксплуатации характеристики технологического процесса могут изменяться в широких пределах. На них оказывает влияние ряд факторов, таких как наличие ресурсов для стабильной работы предприятия, психологический климат в коллективе, состояние здоровья работников, занятых в данном производстве и т.п. Таким образом, доход, получаемый от реализации конкретного варианта технологического процесса, будет величиной случайной, зависящей от большого количества факторов.
То же можно сказать и в случае решения задачи выбора варианта структуры системы управления. Допустим, что проектные документы гарантируют некоторые характеристики качества функционирования системы, такие как быстродействие системы, объем информации, передаваемой по каналам связи, объемы памяти и т.д. Но необходимо отдавать отчет в том, что эти характеристики являются средними. Они могут существенно меняться в зависимости от характеристик конкретных технических средств, например, характеристик надежности. Так, частые отказы одной системы приводят к снижению характеристик качества, в то время как надежная работа другой системы позволяет поддерживать ее характеристики качества на достаточно высоком уровне. В данном случае вектор дохода, получаемого от эксплуатации системы, будет величиной случайной, зависящей от вероятности безотказной работы технических средств (впрочем, как и от ряда других факторов).
Функции полезности.
Таким образом, величина дохода, получаемого от реализации того или иного варианта решения, является случайной величиной, зависящей от различных факторов. В случае благоприятного стечения факторов можно получить максимальный доход от выбора определенной альтернативы. В случае неблагоприятного стечения факторов получают минимальный доход. Естественно, что будет некоторое количество промежуточных доходов, зависящих от вероятности реализации того или иного набора факторов.
Поскольку доходы могут иметь различное выражение (денежное выражение дохода, быстродействие системы, объем памяти и т.п.) необходимо обеспечить возможность их сравнения. Как было указано ранее нужно иметь систему предпочтений, систему весовых коэффициентов, с помощью которых можно было бы производить сравнение вариантов реализации различных альтернатив, когда они описываются векторными системами доходов. В качестве такой системы предпочтений выступает функция полезности. Для всякого распределения Ре Хи всякой вещественной функции q на множестве R обозначим через E{glP) математическое ожидание функции q (если оно существует) относительно распределения Р. Другими словами
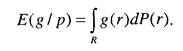
Вещественная функция g, заданная на множестве R, называется функцией полезности, а для любого дохода г е R число g(r) называется полезностью г. Для всякого распределения Р е 9? число E(g/P) называ-1 ют полезностью Р или средней полезностью.
Определение функции потерь
Рассмотрим теперь пространство X всех возможных решений х, а R пространство всех возможных доходов г, которые может получить исследователь в результате решения х и исхода у. Доход из R, получаемый исследователем при решении х и исходе у обозначим через о(х, у). Будем считать заданным вероятностное распределение Р на пространстве исходов Y, причем значение Р(у) определено для каждого исхода у. Предположим также, что на множестве R задана функция полезности.
Для всякого вероятностного распределения Рх, для которого функ-ция g интегрируема, среднюю полезность E{glP) можно вычислить по формуле
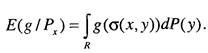
Тогда задача исследователя будет состоять в выборе решения х, максимизирующего E{glP).
В задачах принятия решения каждому доходу г е R принято сопоставлять не полезность, а потери. Функция потерь определяется равенством
L(x, у) = -g(o(x, у)).
При любом (х, у) число L(x, y) представляет собой ущерб исследователя от принятия решения х, в случае, когда реализовался исход у. Пусть Р - вероятностное распределение исхода у. При всяком решении х средний ущерб р(Р, х) называется риском и определяется по формуле
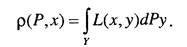
В этом случае системный аналитик должен стремиться к выбору решения х, минимизирующего риск р(Р, х). Таким образом, сформировано правило выбора решения в случае, когда на пространстве исходов задано распределение вероятностей.
Задачи решения с наблюдениями
Рассмотрим задачи решения, в которых исследователь перед тем как выбрать решение из множества X, наблюдает значение случайной величины или случайного вектора z, связанного с исходом у. Наблюдение z дает исследователю некоторую информацию о значении у, которая помогает ему принять рациональное решение. Будем полагать, что для всех у е Y задано условное распределение z.
Поскольку решение исследователя зависит от наблюдаемого значения z, он должен выбрать решающую функцию 8, задающую для любого возможного значения z & Z решение 8(z) e X. В этом случае функция риска будет определяться равенством
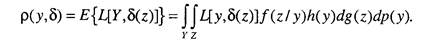
Термин «риск» здесь как и ранее относится к среднему ущербу. Для каждого решения х е Хр(у, 5) обозначает риск от принятия решения х. Распределение h(y) называется априорным, так как оно задает распределение у до проведения наблюдения над z.
Цена наблюдения
В задачах принятия решений наблюдение случайной величины z связано с определенными затратами, которые должны учитываться аналитиками, проводящими системные исследования, при расчете риска от принятия решающей функции, использующей результаты наблюдения z. Это обстоятельство играет особенно важную роль в случае, когда аналитику надо решить, какую из нескольких случайных величин предпочтительнее наблюдать, или ответить на вопрос, производить ли наблюдения вообще. Пусть с(у, z) обозначает цену наблюдения значения z из множества Z. Тогда, если h(y) есть априорная плотность распределения случайной величины у, то средняя цена наблюдения равна
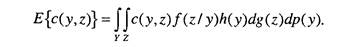
Будем предполагать, что для цены с(у, z) верно предположение о средней полезности. Иными словами, будем считать, что эта цена выражена в соответствующих единицах отрицательной полезности так, что существенным является лишь среднее значение вероятностного распределения цены.
Общим риском от наблюдения z и принятия решающей функции 8 называется сумма риска р(у, 5) и средней цены наблюдения Е{с(у, z)}. Системный аналитик должен выбрать наблюдением из некоторого класса доступных наблюдению случайных величин и соответствующую решающую функцию 5(z) е X, минимизирующую общий риск. Условное распределение у при известном значении z называется апостериорным распределением у, так как оно задает распределение у при зафиксированном значении z.
Сформировав общий риск от наблюдения можно решать задачу о необходимости проведения наблюдений. Если общий риск от наблюдения оказывается меньше, чем риск р(Р, х), получаемый без проведения дополнительных наблюдений, то наблюдения есть смысл проводить, если же общий риск оказывается больше риска р(Р, х), то организовывать дополнительные наблюдения смысла не имеет. Таким образом, организовывать наблюдения имеет смысл лишь в том случае, когда цена наблюдения меньше выигрыша, получаемого за счет поступления новой информации.
В рассмотренных задачах делалось предположение о том, что на пространстве решений Хи пространстве исходов Г заданы соответствующие распределения. Если вид закона распределения определяющего параметра считается известным, то применение описанных процедур осуществляется согласно приведенным формулам. Если же информации о виде закона распределения у исследователя нет, приходится отказываться от применения параметрического подхода. Здесь важно отметить, что приходится отказываться от необходимости знать вид распределения, а не от того что выборка подчинена какому-то, пусть неизвестному, но существующему закону распределения. Предположение о статистичности наблюдений остается в силе. В этом случае для описания распределения на множествах решений и исходов следует применять непараметрические методы.
Незнание функционального вида распределения не означает, что исследователь ничего не может сказать о свойствах распределения. Результаты специально организованных наблюдений, информация, полученная из эксплуатации объекта системного анализа, на этапе его реального функционирования, служит основой для построения непараметрических процедур, решающих задачу выбора. Методы обработки статистических данных с использованием непараметрических процедур рассмотрены ранее [56].
Остановимся на сложностях, которые необходимо осознавать при решении реальных задач выбора, т.е. когда теоретические методы применяются на практике. Неудачное или неправильное применение статистических методов к решению реальных проблем может привести к отрицательному результату. Причины неправильного применения статистических методов известны. Рассмотрим их
1. Статистический вывод по своей природе случаен, поэтому он никогда не может быть абсолютно достоверным. Поэтому при решении задач выбора любая процедура должна сопровождаться оценкой характеристик ее качества. При оценке параметра необходимо вычислять точность, характеризуемую, например, дисперсией. При проверке гипотез необходимо оценивать мощность критерия, с помощью которого осуществляется проверка, вычислять ошибки первого и второго рода. При повышении требований к качеству принимаемых решений необходимо организовать дополнительные исследования объекта системного анализа и тем самым увеличивать объем информации, на основании которой осуществляется принятие решения. Статистический вывод может быть ошибочным, но всегда имеется возможность варьировать характеристики ошибок.
2. Качество решения, принимаемого с помощью процедур статистического вывода, существенно зависит от информации, поступающей на вход. Какие данные в модель заложить, такое решение и получим. В реальной эксплуатации сложных систем встречаются ситуации, когда обслуживающий персонал умышленно скрывает информацию, не записывая все события, происходящие с объектами в оперативные журналы. Например, персонал не заинтересован в ведении журналов учета отказов объектов, так как эффективность функционирования объектов напрямую связана с материальными вознаграждениями персонала. Если они будут записывать все отказы, то это повлечет за собой лишение премий. Естественно, что принятие решений, связанные с планированием деятельности предприятия на основании такой неполной информации будет заведомо содержать ошибку.
3. Отрицательный результат применения теории статистических выводов может быть получен в тех случаях, когда природа явлений, относительно которых принимается решение, не имеет статистического характера. Иными словами встречаются ситуации, когда статистической обработке подвергаются данные, не имеющие статистической природы. Иногда этот факт трудно проверить, особенно при малых объемах выборки. Выяснению факта наличия статистической природы рассматриваемых явлений или процессов следует уделять специальное внимание при организации наблюдений или экспериментов.
4. Снижение кач
|