Моделей

5.1. Модели и виды подобия

Исследование систем с помощью моделей может быть обосновано только в том случае, когда модель адекватно описывает процессы и явления, происходящие в системах. При использовании моделей необходимо теоретически обосновать аналогию между моделью и реальным физическим явлением. Только в этом случае результаты, полученные на модели, могут быть перенесены на исследуемый объект. Без этого обоснования моделирование теряет познавательное значение, так как перестает быть достоверным источником информации о реальных явлениях и процессах. В основе доказательства степени соответствия модели и объекта лежит теория подобия. Необходимо отдавать отчет в том, что абсолютное подобие может иметь место только лишь при замене одного объекта другим, точно таким же. При моделировании абсолютного подобия добиться невозможно. Системные аналитики стремятся к тому, чтобы модель достаточно хорошо отображала исследуемую сторону функционирования объекта.

В предыдущих главах были рассмотрены основные понятия моделей, методы построения моделей систем, организация имитационного моделирования как метода проведения системных исследований. Остановимся еще раз на понятии моделирования с точки зрения теории подобия. Моделирование представляет собой процесс проведения исследований объекта, базирующийся на подобии модели и объекта, и включает в себя построение модели, ее изучение и, наконец, перенос полученных результатов на объект исследования. Под моделью понимают объект, например, явление, процесс, систему, экспериментальную установку, знаковое образование, математические выражения, находящиеся в отношении подобия к исследуемому объекту. Математическое моделирование использует подобие между величинами, входящими в ма-

тематические выражения, описывающие поведение изучаемого объекта. Иначе говоря, в математическом моделировании в отличие от других форм моделирования предполагается замена явления его математическим описанием, воспроизводимым вычислительными средствами.

Физическое моделирование использует подобие между объектом и моделью, имеющей физическую природу. Основой физического или математического экспериментального исследования являются методы теории подобия, которые применяются при постановке эксперимента, обработке данных о результатах экспериментальных исследований и испытаний.

В процессе проведения системных исследований необходимо решать вопросы измерения характеристик и обработки статистических данных, распространения полученных данных на другие явления, выбора аналогов при проектировании систем, повышении точности и достоверности оценок рассчитываемых характеристик исследуемых объектов. Перечисленные вопросы решаются с помощью методов теории подобия, которая дает ответы на ряд вопросов о том, как организовать исследования и испытания объекта анализа, как обрабатывать опытные данные, обобщать и распространять полученные результаты на другие объекты.

Модель и отображаемый ею объект находятся в отношении сходства, а не тождества. Это означает, что модель по определенным признакам подобна изучаемой системе, а по каким-то может быть от нее отлична. Важное условие при проведении исследований - реализовать подобие по наиболее важным признакам с точки зрения проведения конкретного, данного исследования. Понятие модели взаимно связано с понятием подобия. Модель обеспечивает подобие тех процессов, которые удовлетворяют критериям, полученным с помощью теории подобия. Характеристики любого явления в группе подобных явлений могут быть реализованы с помощью критериев подобия путем некоторого преобразования характеристик другого подобного явления. Примером такого преобразования может служить масштабирование.

Подобие определяют как взаимно однозначное соответствие между двумя объектами, при котором функции перехода параметров, характеризующих один из объектов, к другим параметрам известны, а математические описания этих объектов могут быть преобразованы в тождественные.

Итак, сформулируем очевидный тезис: чтобы некоторая конструкция могла быть отражением, т.е. замещала в некотором смысле оригинал, между оригиналом и моделью должно быть установлено отношение подобия. Существуют разные виды подобия. Первый тип подобия - это подобие, устанавливаемое в результате физического взаимодействия в процессе создания моделей. Приведем примеры такого подобия. Прежде всего, это масштабированные модели гидротехнических сооружений, самолетов, кораблей, автомобилей, макеты зданий и т.п. Такое подобие называется прямым. Только при прямом подобии возможна взаимозаменяемость модели и оригинала. Но даже в случае проведения исследований на модели, которая является макетом, созданным путем реализации отношения прямого подобия, возможны сложности с переносом результатов моделирования на оригинал. Например, при исследовании влияния водной среды на гидротехнические сооружения можно промасштабировать не только само сооружение, но и часть условий, в которых проводятся исследования (скорость течения воды, высоту волн), однако часть факторов масштабированию не поддается, например, вязкость воды, сила тяготения. В результате задача пересчета данных, полученных при проведении модельного эксперимента, на реальные условия становится нетривиальной.

Второй тип подобия - косвенное подобие. Косвенное подобие объективно существует в природе, обнаруживается в виде совпадений или достаточной близости оригинала и модели. Если установлена близость абстрактных моделей рассматриваемых объектов (оригинала и модели), то можно переходить к использованию их в практике реального моделирования. Наиболее известным примером косвенного подобия является подобие некоторых электрических и механических процессов, описываемых одинаковыми уравнениями. Различие в уравнениях состоит лишь в различной физической интерпретации переменных, входящих в эти уравнения. Рассмотрим примеры сходства математических описаний процессов различной физической природы: электрических, механических, гидравлических, процессов динамики жидкости и газа и пр. (табл. 5.1).

Законы Кулона и Ньютона описывают силу, действующую на единичные электрические заряды q_x и q₂ или тела, массой /я, и т₂, находящиеся друг от друга на расстояниях г, достаточно больших по сравнению с геометрическими размерами несущих их тел.

Уравнения электрической и гидравлической цепей описывают поведение потока зарядов (электрического тока/) и потока жидкости (гидравлического тока J) сквозь электрические и гидравлические сопротивления r_e, r, индуктивности L_e, L_g и емкости С,, С,. В этом случае аналогом напряжения электрической цепи является давление Р в расчете на единицу объемной плотности р_т текущей среды, заполняющей гидравлическую цепь.

Таблица 5.1

Принципы непрерывности электрического тока и неразрывности жидкости означают, что суммарный поток зарядов J и суммарный ток жидкости/, проходящие в единицу времени сквозь любую замкнутую поверхность S, в точности равны скорости изменения соответственно заряда или массы внутри этой поверхности. Эти принципы представляют собой законы сохранения вещества (заряда или массы) при любых преобразованиях, кроме аннигиляции.

Из закона сохранения энергии в установившемся режиме течения следует, что плотность полной электрической W или механической Р энергии постоянна вдоль всей цепи, хотя и может перераспределяться между потенциальной, кинетической и тепловой формами. В уравнениях используются обозначения: р_е и р_т - объемные плотности заряда и массы; g - ускорение в поле земного тяготения; h - расстояние от источника электрической энергии до данного места цепи или высота уровня жидкости над данным местом гидравлической цепи соответственно; к_е - коэффициент, характеризующий геометрию цепи; v - скорость течения зарядов или жидкости.

Убедившись в схожести описаний процессов различной физической природы, можно заменить исследования одних из них изучением других. Так, вместо громоздкого и сложного экспериментирования с механическими объектами можно проводить опыты с электрической схемой, исследовать при этом различные варианты, не переделывая механическую конструкцию. Примером косвенного подобия является проведение исследований на аналоговых вычислительных машинах. В свое время масштабы использования аналоговых вычислительных машин были очень широки.

Третий класс моделей - это модели, подобие которых оригиналу не является ни прямым, ни косвенным, а устанавливается в результате соглашения. Такое подобие называется условным. Примерами условного подобия являются чертежи (модели будущих объектов), карты (модели местности), сигналы (модели сообщений). Условное подобие не требует фактического сходства, но несмотря на это, оно должно строиться с учетом особенностей человека - создателя и потребителя моделей условного подобия.

5.2. Основные понятия физического подобия

Виды физического подобия

Теория подобия включает в себя такое обширное понятие как физическое подобие, которое объединяет геометрическое, динамическое, кинематическое, тепловое и другие виды подобия. При геометрическом подобии отношение любых сходных отрезков равно одному и тому же постоянному числу. Иными словами изучаемый объект подобен первоначальному, когда он получается путем изображения его в другом геометрическом масштабе. Кинематическое подобие означает, что в любых сходных точках систем скорости движущихся объектов параллельны и пропорциональны друг другу, т.е. отношение между их скоростями одинаково во всех точках системы. Если система рассматривается как состоящая из отдельных элементов, то у подобных систем отношение масс элементов между собой представляет постоянное число. Динамическое подобие заключается в параллельности и пропорциональности сил в сходных точках. Тепловое подобие означает пропорциональность друг другу всех характеризующих тепловое явление величин: температур, теплоемкостей, тепловых потоков, коэффициентов теплопроводности и т.д.

Приведем математическую формулировку подобия. Введем обозначения. Пусть /j и /₂ - сравниваемые отрезки длин первого и второго объектов, Vj и v₂ - скорости объектов, т, и т₂ - массы, ^ и/₂ - сравниваемые силы. Тогда можно записать

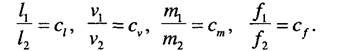
Коэффициенты, определяющие отношения длин с, скоростей с, масс с_т и сил с, называются константами подобия. Для каждого вида величин константы имеют свою особую численную величину.

В общем случае подобие явлений, процессов или систем определяется как пропорциональность друг другу всех величин, характеризующих данные объекты. Коэффициенты пропорциональности при этом сохраняют постоянное значение во всех точках системы для величин определенного наименования, но могут принимать отличные значения для величин разного наименования.

Подобных объектов может быть не два, а значительное количество, т.е. они могут составлять группу подобных объектов. Сравнивая все члены группы с одним объектом, который является образцовым или базовым, можно выявить закономерность: при переходе от одного, подобного базовому, объекта к другому константы подобия могут принимать разные значения. Но при этом сохраняется свойство постоянности констант во всех точках каждой системы, подобной базовому образцу. Объединяя переход от явлений образца ко всем подобным ему, можно рассматривать его выражение х'₂ =c_xix[ как групповое преобразование явления.

Инварианты подобия

Подобие явлений можно выражать не только константами подобия, но и так называемыми инвариантами подобия. Для пояснения понятия инварианта подобия необходимо перейти от абсолютной системы единиц измерений к относительной. С этой целью требуется отнормиро-вать все величины каждого из подобных объектов. При этом за базовое значение принимаются характеристики объектов, измеренные в сходных точках, например, объект характеризуется линейными размерами длиной /,, шириной d_x и высотой А,. Возьмем один из параметров за базовый, остальные отнормируем относительно него, получим

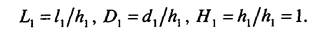
Аналогичные действия проведем для объекта, находящегося в отношении подобия к первому объекту, при этом в качестве базового возьмем аналогичный параметр, что и для первого объекта, в нашем случае это высота. В результате получим

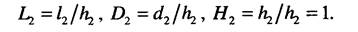
Поскольку первый и второй объекты находятся в отношении подобия, то для них выполняется условие /, //₂ =djd₂ =hjh₂ =c_n откуда получаем

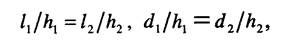
следовательно L_X⁼L_V D=D_r Точно такие же соотношения можно получить для любых других характеристик объектов, находящихся в отношении подобия друг к другу. Так для скоростей процессов будем иметь

^v! /^vi° ^{= v}i - ^V2 /^V2 = ^Vi > ^гД^е нижний индекс означает номер объекта, а верхний индекс - номер точки, в которой производятся измерения: при этом одинаковыми индексами обозначены результаты измерений в сходных точках. Проводя такую же процедуру, как это было сделано в случае линейных размеров, получим Vj' = V₂'. Для масс объектов будет справедливо выражение М/ = М₂'. Таким образом, получен результат, заключающийся в том, что значения соответствующих характеристик подобных объектов, выраженные в относительных единицах измерения и рассчитанные в сходных точках, равны друг другу. Эти величины и называются инвариантами подобия.

Необходимо различать понятия «константа подобия» и «инвариант подобия». Константа сохраняет постоянное значение во всех точках системы, но она изменяется, когда одна пара подобных явлений заменяется другой. Инвариант подобия, наоборот, различен для разных точек системы, так как он является отображением одной из величин этой системы, имеющей разное численное значение в разных точках системы. Инвариант подобия не меняется при переходе от одного явления к любому другому, подобному ему, т.е. сохраняет одно и то же значение в сходных точках всей группы подобных явлений.

Константы подобия не являются произвольными величинами. Характер взаимосвязи величин, входящих в константы подобия, определяется закономерностью физического явления и выражается в виде уравнений. Наличие взаимосвязи между величинами налагает определенные ограничения и на константы подобия.

Различают полное, неполное, приближенное и другие виды подобия, используемые в соответствующих способах моделирования. Полное подобие и соответственно способ моделирования в формализованном виде характеризуют тот случай, когда между всеми параметрами образцового объекта и модели выполняется соотношение у. = тх., где у. - i-й параметр системы-оригинала; х. - i-й параметр модели; т. - масштабный коэффициент, который обычно является постоянной величиной.

Неполное подобие и соответственно способ моделирования характеризуются частичным подобием протекания основных процессов в системе и модели или только в пространстве, или только во времени. Приближенное подобие имеет место в том случае, когда для части параметров системы и модели инварианты подобия приблизительно равны друг другу, т.е. значения инвариантов системы и модели укладываются в некоторые границы критической области.

Совокупность масштабных коэффициентов перехода от модели к натурному образцу представляет собой масштабный фактор системы в целом. Изменение масштабного коэффициента перехода от модели к образцу для одного из параметров приводит, как правило, к изменению масштабного фактора физической системы пропорционально значению этого параметра для исследуемого процесса. В сложной неоднородной системе при расчете масштабного фактора должны учитываться взаимовлияния подсистем. При этом необходимо обращать внимание на проверку критериев подобия в широком диапазоне изменения параметров в процессе проведения исследований. Для однородных моделей, полученных на основе теории подобия, как правило, выполняются требования автомодельности. Автомодельность - это свойство явления автоматически сохранять подобие явлению-оригиналу независимо от абсолютных величин параметров элементов той или иной системы, в которой данное явление протекает. Согласно теории подобия, если модель и натурный объект подобны, то они описываются одинаковыми критериями и эти критерии тождественны. Если отношения подобия между моделью и оригиналом установлены, то результаты, полученные при исследовании модели, можно переносить на объект-оригинал.

5.3. Формирование критериев физического подобия

До сих пор речь шла об установлении подобия объектов на основании сравнения определяющих параметров, характеризующих свойства сравниваемых объектов. Однако в теории подобия известны результаты, которые говорят о том, что количество сравниваемых величин можно уменьшить, сформировав так называемые критерии подобия. Критерием подобия к назовем безразмерный (т.е. нулевой размерности) функционал, зависящий от нескольких определяющих параметров объекта (двух и более):

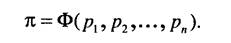
Рассмотрим способ формирования критериев подобия для некоторого явления, процесса или системы. Пусть рассматриваемый объект характеризуется п параметрами/^, р₂,.. ., р_п. Каждый параметр представляет собой некоторую измеримую физическую величину, для которой определена шкала измерения и установлена размерность. Размерность величины находится при помощи определительного уравнения, которое описывает эту величину в математической форме. Например, определительное уравнение для скорости имеет вид v-dLI dT, где L - расстояние; Г- время; для силы F - Mg, где M, g- соответственно масса и ускорение. Размерность величины будем указывать при помощи символа, взятого в квадратные скобки, так, например, для размерности скорости движения объекта запишем [v] = [L][7]', где [L], [7] - соответственно размерности длины и времени; для размерности силы получим [F] = [M][L][7]" ², где \М\ - размерность массы. Короче говоря, размерность любой физической величины представляет собой произведение возведенных в степень размерностей первичных величин.

Рассмотрим механические системы, для которых первичными единицами измерения являются длина [L], время [7] и масса [М\. Размерность любого определяющего параметра можно выразить через эти единицы:

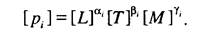
Критерий подобия определим как комбинацию величин p., i = 1, п, т.е. п = pi¹ p% —р^, или выразив через размерности соответствующих величин, будем иметь:

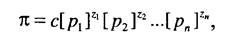
где с - безразмерная величина, численно равная произведению значений параметров. Выразив далее размерность определяющих параметров системы через первичные единицы измерения и подставив эти выражения в критерий подобия, получим:

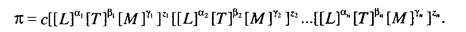
Группируя выражения одной размерности, получим

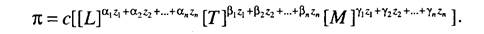
Поскольку критерий подобия был определен как безразмерный функционал, можно записать соотношение, связывающее степени у размерностей:

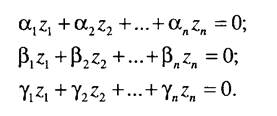
Получена система из трех уравнений. Ранг системы равен трем; таким образом, число независимых переменных равно п-r, где г - количество первичных величин, определяющих систему единиц измерения, в рассматриваемом примере г = 3. Это число независимых переменных определяет количество критериев подобия, необходимых и достаточных для решения задачи о подобии оригинала и модели.

Таким образом, для определения критериев подобия необходимо выявить число определяющих параметров, которые характеризуют исследуемый процесс, составить матрицы размерностей каждого параметра, установить число независимых между собой параметров, представить описание исследуемого явления в критериальной форме, записать выражения критериев подобия. Проиллюстрируем формирование критериев подобия на примере системы вынужденных механических колебаний с демпфированием. Пусть груз массой М колеблется на пружине жесткостью С, причем при перемещении его на расстояние / в вязкой среде появляется сила сопротивления, пропорциональная скорости v: F_c= -Kv. На груз действует возмущающая CHnaF_b=Fsin((Ot). Участвующих величин семь: р_х = М, р₂= со, р₃ = F, р_А = I, р₅ = К, р₆= С, р_п = t. Функциональная зависимость, подлежащая исследованию, имеет вид Ф(М, О), F, I, К, С, t). Выберем три независимые единицы применительно к системе измерений LMT. Пусть р_х=М, р₂~ со_о, p₃ = F_Q, тогда получаем систему

Для остальных параметров будем иметь

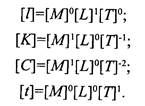
Правильность выбора числа независимых параметров проверяется путем вычисления определителя, составленного на основании системы (5.1):

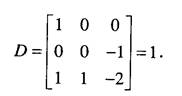
Поскольку определитель не равен нулю, то выбранное значение числа независимых параметров, равное трем, оказывается верным, и величины М, со, F_Q действительно независимы. Дальнейшие действия заключаются в определении формы записи критериев подобия согласно системе уравнений (5.1) и отыскании числовых значений показателей степеней в выражении для размерностей соответствующих параметров. Применительно к данному примеру будем иметь

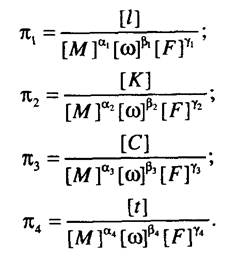
Определим значения показателей степеней ос., р\, %. Выразив размерность каждой из составляющих, входящих в формулы приведенной системы, через первичные единицы измерения, получим

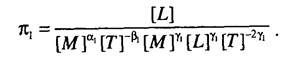
Приравнивая показатели одноименных первичных единиц измерения, стоящих в числителе и знаменателе, получим у= 1, ос, = -1, Р, = -2. Далее для второго критерия

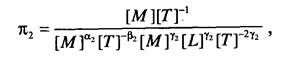
откуда получаем у₂ = 0, а, = 1, Р₂ = 1. Для третьего критерия

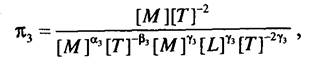
и можно определить показатели степеней у₃=0, < х₃-1, р₃-2. И, наконец, для последнего критерия

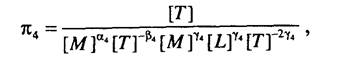
показатели степеней равны у₄= О, (Х₄= 0, |3₄= -1. Критерии подобия, таким образом, будут иметь следующий вид:

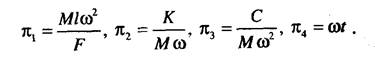
Поскольку в рассматриваемой системе имеется семь определяющих параметров, а выделено четыре независимых критерия, то можно сказать, что на основании данных критериев подобия имеется возможность сформировать новые группы независимых между собой критериев. Имеется в виду независимость критериев внутри группы. Критерии, взятые из разных групп, будут зависимыми. Новую группу независимых критериев можно построить, например, перемножив некоторые критерии из исходной группы.

Таким образом, показано, что для решения задачи определения подобия объектов (оригинала и модели) сравнивается не множество определяющих параметров, а множество критериев, размерность которого меньше, чем размерность множества определяющих параметров.

5.4. Элементы статистической теории подобия

В общем случае параметры исследуемых систем, процессов или явлений могут представлять собой случайные величины. Поэтому необходимо применять основные положения теории подобия с учетом стохастического характера процессов и явлений, происходящих в объектах. Принципы подобия в стохастическом смысле основаны на том, что сравниваемые параметры являются случайными величинами, а критерии подобия - функциями этих случайных величин.

Рассмотрим постановку задачи определения подобия системы-оригинала и модели. Пусть имеется соотношение [29] вида

где р, =, / = 1, т - статистики критериев, сформированные для каж-

дой группы одноименных параметров; {х_х. } - параметры системы-оригинала; {х₂.} - параметры модели.

Считается, что системы подобны, если отношение (5.2) равно единице. Параметры, входящие в выражение (5.2), в общем случае являются случайными величинами. В такой постановке можно говорить о равенстве критерия р единице только с некоторой долей вероятности. Если критерий р является непрерывной случайной величиной, то вероятность того, что р = 1, в точности равна 0. В стохастической постановке принято считать, что две системы подобны, когда функции распределения параметров, характеризующих эти системы, равны, а статистика критерия подобия находится в пределах верхней и нижней границ Доверительного интервала. Вектор параметров системы в общем случае представляет собой набор функциональных и конструктивно-технологических параметров системы. Примерами таких параметров могут служить физические характеристики: коэффициент теплопередачи, рабочее давление, число оборотов вала турбины, параметры, характеризующие габаритные размеры объекта и т.п. В качестве параметров могут использоваться обобщенные параметры, например, характеристики надежности типа среднего времени до отказа (наработка на отказ), коэффициент готовности, вероятность выполнения задачи и т.д.

Примеры параметров промышленных объектов. Проведем анализ параметров на примере конкретных промышленных объектов. Рассмотрим агрегаты, входящие в структуру атомных электростанций (АЭС). Так при анализе модульных парогенераторов АЭС определяющими параметрами являются количество трубок в модуле, количество модулей, длина трубки, толщина стенок трубки, коэффициент теплопередачи, параметры рабочего тела. При исследовании подобия турбин определяющими параметрами являются мощность турбины, габаритные размеры, параметры пара, такие как влажность, температура и пр. Для электронных устройств помимо конструктивного подобия необходимо анализировать электрические параметры: напряжение и силу тока на входе и выходе, коэффициент усиления и т.п.

Изложим способ получения численного значения статистик критерия подобия. Пусть случайные параметры х„, х, ₂,..., jc_lm имеют плотность распределения/„(*,.), соответственно параметры х₂₁, x₂₂,..., х_2т имеют плотность/^.(х₂.). Тогда в терминах задачи проверки статистических гипотез нулевая гипотеза Н_о будет состоять в том, что/,.(х,.) ~/₂₁(^х₂) для всех одноименных параметров.

Альтернативная гипотеза заключается в том, что/,.(х,.) ^f₂fx₂)- Для критерия подобия можно записать, что сравниваемые системы подобны, если р е [р_п, р J. Здесь p_n, p_fe - соответственно нижняя и верхняя границы доверительного интервала для критерия подобия, определяемые с некоторым уровнем значимости.

Для определения численного значения статистики критерия р при справедливости гипотезы Н_о необходимо по известным плотностям распределения случайных величин х,. и х₂. определить плотности распределения/,.(х,.) и/₂.(х₂.), от этих плотностей перейти к плотности распределения величины р и, наконец, вычислить выборочное значение статистики р и границы критической области [р_п, р_ь].

Итак, пусть каждый объект характеризуется некоторым числом параметров х., i=l, т. Перепишем формулу (5.2) в следующем виде:

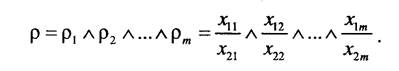
Иными словами сравнению подлежат параметры одного типа. Например, сравнивают длину трубок парогенераторов оригинала и модели, толщину стенок этих парогенераторов, их теплопроводность и т.д.

Множество величин р. представляет собой набор независимых случайных величин. Тогда объекты - оригинал и модель - находятся в отношении подобия, если они подобны по каждому определяющему параметру.

Теперь задача сводится к определению доверительного интервала по каждому критерию подобия р₍ с одним и тем же уровнем значимос-. ти. Если такие интервалы найдены и для каждого критерия выполняются условия ре [p_n, pj, то объекты можно считать подобными. Если же хотя бы по одному критерию условие подобия не выполняется, то оснований считать объекты подобными нет.

Следует заметить, что часть анализируемых параметров может иметь детерминированный характер. Так, в примере с парогенератором можно считать, что длина трубок, толщина стенок трубок - величины неслучайные, поэтому при анализе подобия объектов по этим параметрам решение тривиальное, не требующее привлечения аппарата случайных функций. Подобие по этим параметрам определяется путем деления параметров объекта-оригинала на соответствующие параметры модели. Таким образом, размерность задачи (5.2), требующей анализа с использованием аппарата случайных функций, существенно понижается.

Методика определения плотности распределения величины р состоит в следующем. Итак р = —— выборочное значение статистики критерия, определенное по результатам испытаний системы оригинала и модели, F_p (к) - функция распределения величины р.. Не нарушая общности, опустим индекс в записи для функции распределения, так как аналогичные выкладки будут иметь место для любых параметров системы, имеющих характер случайных величин. Запишем выражение для функции распределения:

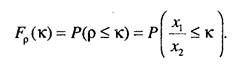
Величины х, и х₂, независимы, следовательно, их совместная плотность распределения есть произведение плотностей этих величин. Соу

гласно [31], вероятность соотношения —^l< k выражается интегралом от совместной плотности по области, определенной неравенствами х> О, х, < х₂к:

Будем считать, что функция F (к) дифференцируема, т.е. существует плотность/(к).

Точные доверительные границы определяются из соотношений

где а -- уровень значимости.

В данных соотношениях неизвестными величинами являются значения границ доверительного интервала р_я, р_ь, относительно которых необходимо решить интегральные уравнения (5.4). Определив функцию распределения статистики критерия (5.3) можно ограничиться вычислением приближенных границ доверительного интервала. Для этого необходимо получить плотность распределения статистики критерия р, вычислить математическое ожидание

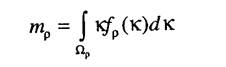
и среднее квадратическое отклонение статистики критерия

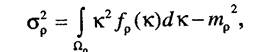
где D - область определения критерия р. В общем случае область определения критерия О. = [О, °о]. Определив математическое ожидание и среднее квадратическое отклонение, можно вычислить приближенный доверительный интервал по формулам р„ = т_р - t_aa_p, р_ь=т_р+ t_ao_p, где t_a - квантиль распределения Стьюдента, определенный для уровня значимости а.

Рассмотрим методику проверки гипотезы о подобии объектов оригинала и модели. Решение о подобии объектов будем принимать на основании сравнения оценок, полученных на различных этапах исследования, а именно, при функционировании объекта-оригинала и при исследовании модели. Особо подчеркнем, что в качестве сравниваемых параметров фигурируют оценки. Поскольку оценки определяются путем обработки выборки случайных чисел ограниченного объема, то они сами являются случайными величинами, имеющими плотность распределения^/). В ряде случаев плотность распределения оценок характеристик довольно просто получить на основании плотности распределения исходной случайной величины. Известно [30], что если оценка характеристики выражается через достаточную статистику М(Т) (через М{Т) в математической статистике принято обозначать сумму случайных величин), то для определения ее плотности распределения можно воспользоваться аппаратом характеристических функций. Такая ситуация имеет место при определении средней наработки, интенсивности отказа, вероятности отказа, коэффициента готовности и ряда других параметров системы. Рассмотрим два случая распределения наблюдаемых случайных величин.

1. Случайная величина (например, наработка до отказа) имеет гамма-распределение t~T(t, А,, а) с параметрами: X - параметр масштаба и а - параметр формы. Определим плотность распределения средней величины. Рассмотрим функционирование объекта-оригинала. Пусть за время его работы наблюдаемая случайная величина реализовалась it раз. Положим, что все случайные величины независимы и распределены по гамма-закону

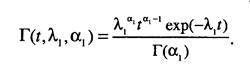
Характеристическая функция для данной плотности имеет вид

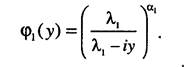
Характеристическая функция величины X = ^7}, где к - объем стати-стических данных, определяется из соотношения

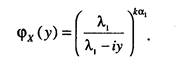
Применяя к данному выражению обратное преобразование Фурье, получаем плотность распределения случайной величины X

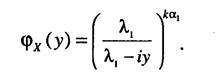
Перейдем от плотности распределения случайной величины X, представляющей собой сумму случайных величин, к величине Г_р, являющейся средней величиной

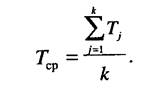
Плотность распределения средней величины будет иметь вид

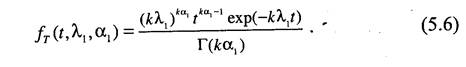
Аналогичное выражение получим для распределения оценки, рассчитанной по результатам испытаний модели:

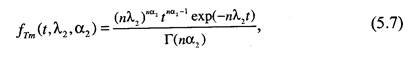
здесь п - объем статистических данных, полученных при проведении исследования модели. Определим теперь функцию распределения статистики критерия р, для чего подставим выражения (5.6) и (5.7) в (5.3) и получим

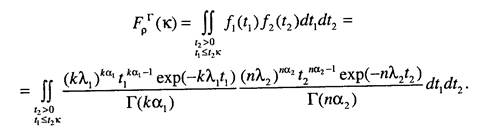
Перейдем в данном выражении к повторному интегралу и произведем замену переменных t₂=v, t_x = uv, получим

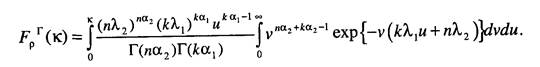
Внутренний интеграл в данном выражении представляется через гамма-функцию следующим образом:

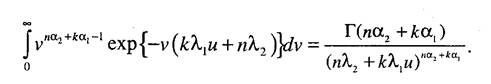
Таким образом, функция распределения критерия р будет иметь вид

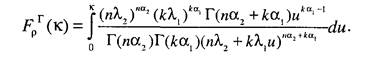
Соответствующая данной функции плотность распределения получается дифференцированием данного выражения по к и равна

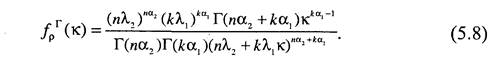
При справедливости гипотезы Н_о должны выполняться соотношения Х, ₁=А.₂=Я,, ос^ос^а, тогда условная плотность распределения статистики критерия будет иметь вид

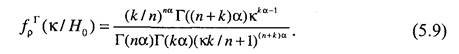
Точные верхнюю и нижнюю границы доверительного интервала р_п, р_ь определяем, решая уравнения (5.4), подставляя в них выражение (5.9). Данные уравнения решаются численными методами, например, методом последовательных приближений. Гамма-распределение является довольно общим распределением. К семейству гамма-распределений относятся распределение Рэлея, экспоненциальное распределение, %²-распределение. Таким образом, полученные результаты могут быть обобщены на ряд других законов распределения случайной величины, для которой формируется критерий подобия.

2. Второй случай характеризует ситуацию, когда наблюдаемые случайные величины подчиняются нормальному распределению. Методику разработки критерия будем рассматривать на примере сравнения средних арифметических выборочных данных, полученных при функционировании оригинала и модели. Пусть наблюдаемые случайные величины имеют плотность распределения соответственно

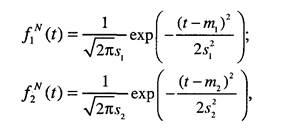
где m_v s - параметры плотности распределения случайной величины, полученной при наблюдении за объектом-оригиналом; т₂, s₂ - параметры плотности распределения случайной величины, полученной при исследовании модели. Тогда выборочные средние значения, определяемые

из выражения X =£ г,., будут иметь соответственно следующие выра-жения для плотностей распределения:

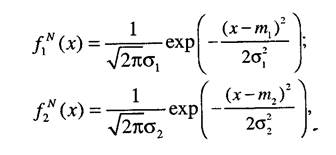
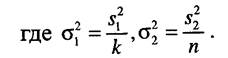
Запишем функцию распределения статистики критерия р:

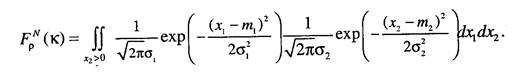
Переходим в данном выражении к повторному интегралу, выполняя при этом замену переменных х₂ - v, х, = uv:

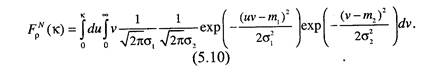
Произведем в данном выражении следующую замену переменных:

пи с, _

ц, = —-, 5 = —-, далее индексы у параметров для простоты опустим. Запишем показатель у экспоненты, предварительно суммируя слагаемые:

Приведем подобные члены в данном выражении:

Разделим числитель и знаменатель на (c²+s²), получим

_ v² - 2у(цо² + ms¹) /(о² + s²) + (|Го² + mV) /(о² + s²) 2s²a²/(o²+s²)

В числителе данного выражения добавим и отнимем величину

, тогда выражение примет вид

В первом слагаемом получили квадрат разности двух выражений, причем выделили переменную v. Второе слагаемое получилось не зависящим от интегрируемой переменной. Упростим второй член данной суммы, для чего вынесем за скобку (c²+s²)'², тогда получим

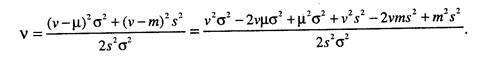
Приведем подобные члены в данном выражении:

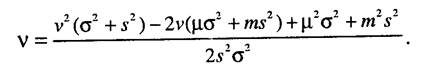
Разделим числитель и знаменатель на (c²+s²), получим

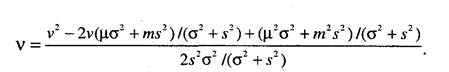
В числителе данного выражения добавим и отнимем величину

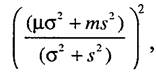тогда выражение примет вид

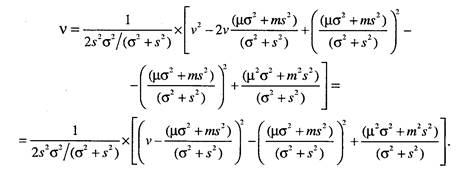
В первом слагаемом получили квадрат разности двух выражений, причем выделили переменную v. Второе слагаемое получилось не зависящим от интегрируемой переменной. Упростим второй член данной суммы, для чего вынесем за скобку (c²+s²)'², тогда получим

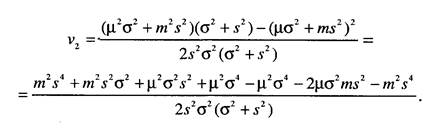
Приведем подобные члены и получим простое выражение

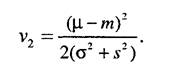
Преобразуем выражение (5.10) с учетом полученных результатов:

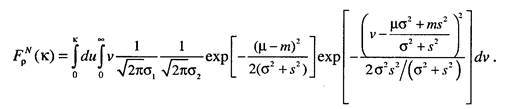
Первая экспонента в данном выражении не зависит от v, поэтому ее можно вынести за знак внутреннего интеграла. Тогда получим

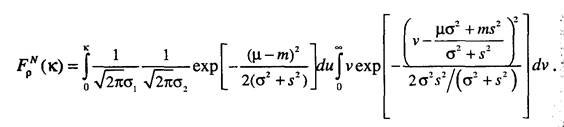
Внутренний интеграл в данной формуле выражается через функцию Лапласа. Покажем это. Для этого введем обозначение:

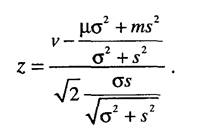
Тогда интеграл можно записать в виде

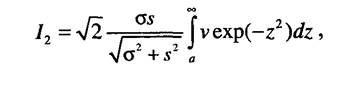
где нижний предел интегрирования равен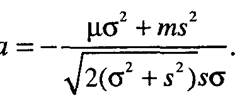

По определению функция Лапласа имеет вид

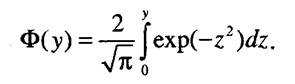
Следовательно, можно записать

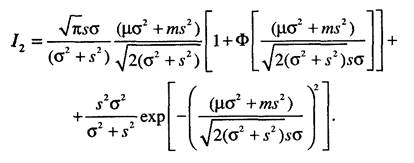
Подставляя полученное значение в (5.10) и переходя к прежним обозначениям, будем иметь

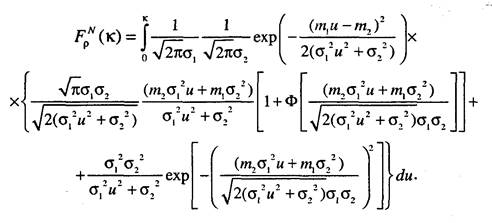
Соответствующая плотность распределения статистики критерия выглядит следующим образом:

При условии справедливости нулевой гипотезы должны выполняться соотношения m, = m₂, s= s_r Следовательно, условная плотность распределения статистики критерия при условии справедливости нулевой гипотезы будет иметь вид

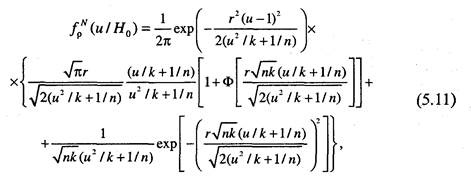
здесь r = m/s.

Зная плотность распределения статистики критерия подобия, можно вычислить по аналогии с предыдущим случаем границы доверительного интервала для заданного уровня значимости. Для этого необходимо подставить выражение (5.11) в (5.4) и решить уравнения относительно верхней и нижней границ доверительного интервала. Нормальный закон распределения также является общим случаем, частными случаями которого будут усеченное нормальное распределение, логарифмическое нормальное распределение.

Таким образом, проверяя по каждой группе одноименных параметров гипотезу о их подобии, решаем задачу подобия системы оригинала и модели.