
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
S Состояние электрона в атоме водорода.
|
|
1 s -Состояние электрона в атоме водорода является сферически-симметричным, т. е. не зависит от углов q и j. Волновая функция y электрона в этом состоянии определяется только расстоянием r электрона от ядра, т. е. y = y 100(r), где цифры в индексе соответственно указывают, что п= 1, l= 0 и ml =0. Уравнению Шредингера для 1 s -состояния электрона в атоме водорода удовлетворяет функция вида
: 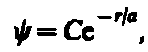
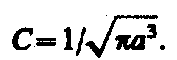
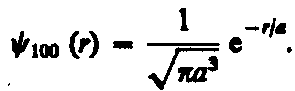
19. Спин электрона. Спиновое квантовое число
Для объяснения тонкой структуры спектральных линий, а также ряда других трудностей в атомной физике американские физики Д. Уленбек (1900—1974) и С. Гаудсмит (1902—1979) предположили, что электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве, спином.
Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.
Если электрону приписывается собственный механический момент импульса (спин) L s, то ему соответствует собственный магнитный момент р ms. Согласно общим выводам квантовой механики, спин квантуется по закону
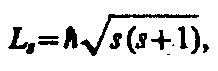
где s — спиновое квантовое число.
20. Принцип неразличимости тождественных частиц. Фермионы и бозоны
Все электроны имеют одинаковые физические свойства — массу, электрический заряд, спин и другие внутренние характеристики (например, квантовые числа). Такие частицы называют тождественными.
Необычные свойства системы одинаковых тождественных частиц проявляются в фундаментальном принципе квантовой механики — принципе неразличимости тождественных частиц, согласно которому невозможно экспериментально различить тождественные частицы.
Принимая во внимание физический смысл величины | y |2, принцип неразличимости тождественных частиц можно записать в виде
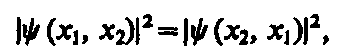
Если при перемене частиц местами волновая функция не меняет знака, то она называется cимметричной, если меняет — антисимметричной.
В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса. Частицы с полуцелым спином (например, электроны, протоны, нейтроны) описываются антисимметричными волновыми функциями и подчиняются статистике Ферми — Дирака; эти частицы называются фермионами. Частицы с нулевым или целочисленным спином (например, p-мезоны, фотоны) описываются симметричными волновыми функциями и подчиняются статистике Бозе — Эйнштейна; эти частицы называются бозонами.
21. Принцип Паули. Распределение электронов в атоме по состояниям
Если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Отсюда следует, что два одинаковых фермиона, входящих в одну систему, не могут находиться в одинаковых состояниях, так как для фермионов волновая функция должна быть антисимметричной. Обобщая опытные данные, В. Паули сформулировал принцип, согласно которому системы фермионов встречаются в природе только в состояниях, описываемых антисимметричными волновыми функциями (квантово-механическая формулировка принципа Паули).
Из этого положения вытекает более простая формулировка принципа Паули, которая и была введена им в квантовую теорию (1925) еще до построения квантовой механики: в системе одинаковых фермионов любые два из них не могут одновременно находиться в одном и том же состоянии. Отметим, что число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется.
Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел:
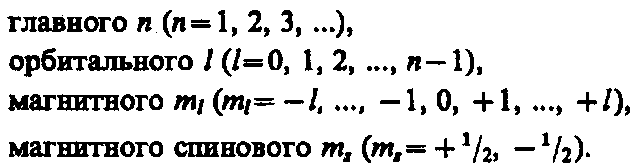
Распределение электронов в атоме подчиняется принципу Паули, который может быть использован в его простейшей формулировке: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел п, l, ml и тs т. е.
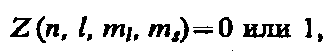
где Z (п, l, ml, тs) — число электронов, находящихся в квантовом состоянии, описываемом набором четырех квантовых чисел: п, l, ml, тs. Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.
Согласно формуле 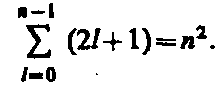 , данному n соответствует n 2 различных состояний, отличающихся значениями l и ml. Квантовое число тs может принимать лишь два значения (± ½). Поэтому максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно
, данному n соответствует n 2 различных состояний, отличающихся значениями l и ml. Квантовое число тs может принимать лишь два значения (± ½). Поэтому максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно
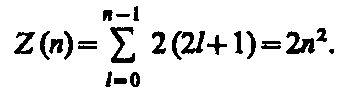
Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному l. Поскольку орбитальное квантовое число принимает значения от 0 до n –1, число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2 l +1).
22. Периодическая система элементов Менделеева
Принцип Паули, лежащий в основе систематики заполнения электронных состояний в атомах, позволяет объяснить Периодическую систему элементов Д. И. Менделеева (1869) — фундаментального закона природы, являющегося основой современной химии, атомной и ядерной физики.
Д. И. Менделеев ввел понятие порядкового номера Z химического элемента, равного числу протонов в ядре и соответственно общему числу электронов в электронной оболочке атома. Расположив химические элементы по мере возрастания порядковых номеров, он получил периодичность в изменении химических свойств элементов. Однако для известных в то время 64 химических элементов некоторые клетки таблицы оказались незаполненными, так как соответствующие им элементы (например, Ga, Se, Ос) тогда еще не были известны. Д. И. Менделеев, таким образом, не только правильно расположил известные элементы, но и предсказал существование новых, еще не открытых элементов и их основные свойства. Кроме того, Д. И. Менделееву удалось уточнить атомные веса некоторых элементов. Например, атомные веса Be и U, вычисленные на основе таблицы Менделеева, оказались правильными, а полученные ранее экспериментально — ошибочными.
Так как химические и некоторые физические свойства элементов объясняются внешними (валентными) электронами в атомах, то периодичность свойств химических элементов должна быть связана с определенной периодичностью в расположении электронов в атомах. Поэтому для объяснения таблицы будем считать, что каждый последующий элемент образован из предыдущего прибавлением к ядру одного протона и соответственно прибавлением одного электрона в электронной оболочке атома. Взаимодействием электронов пренебрегаем, внося, где это необходимо, соответствующие поправки. Рассмотрим атомы химических элементов, находящиеся в основном состоянии.
Единственный электрон атома водорода находится в состоянии 1 s, характеризуемом квантовыми числами п= 1, l= 0, ml =0 и ms =± ½; (ориентация его спина произвольна). Оба электрона атома Не находятся в состоянии 1 s, но с антипараллельной ориентацией спина. Электронная конфигурация для атома Не записывается как 1 s 2(два 1 s -электрона). На атоме Не заканчивается заполнение K -оболочки, что соответствует завершению I периода Периодической системы элементов Менделеева.
Третий электрон атома Li (Z =3), согласно принципу Паули, уже не может разместиться в целиком заполненной K -оболочке и занимает наинизшее энергетическое состояние с n =2 (L -оболочка), т.е. 2 s -состояние. Электронная конфигурация для атома Li: 1 s 22 s. Атомом Li начинается II период Периодической системы элементов. Четвертым электроном Be (Z =4) заканчивается заполнение подоболочки 2 s. У следующих шести элементов от В (Z= 5 ) до Ne (Z= 10) идет заполнение подоболочки 2 р. II период Периодической системы заканчивается неоном — инертным газом, для которого подоболочка 2 р целиком заполнена.
Одиннадцатый электрон Na (Z =11) размещается в М -оболочке (n =3), занимая наинизшее состояние 3 s. Электронная конфигурация имеет вид 1 s 22 s 22 p 63 s. 3 s -Электрон (как и 2 s -электрон Li) является валентным электроном, поэтому оптические свойства Na подобны свойствам Li. С Z= 12 идет последовательное заполнение M -оболочки. Аr (Z =18) оказывается подобным Не и Ne: в его наружной оболочке все s- и p -состояния заполнены. Аr является химически инертным и завершает III период Периодической системы.
Девятнадцатый электрон К (Z =19) должен был бы занять 3 d -состоянис в M -оболочке. Однако и в оптическом, и в химическом отношениях атом К схож с атомами Li и Na, которые имеют внешний валентный электрон в s -состоянии. Поэтому 19-й валентный электрон К должен также находиться в s -состоянии, но это может быть только s -состояние новой оболочки (N -оболочки), т. е. заполнение N -оболочки для К начинается при незаполненной M -оболочке. Это означает, что в результате взаимодействия электронов состояние n =4, l =0 имеет меньшую энергию, чем состояние n =3, l= 2. Спектроскопические и химические свойства Са (Z =20) показывают, что его 20-й электрон также находится в 4 s -состоянии N -оболочки. В последующих элементах происходит заполнение M -оболочки (от Sc (Z= 21) до Zn (Z =30)). Далее N -оболочка заполняется до Кr (Z =36), у которого опять-таки, как и в случае Ne и Аr,
s- и p -состояния наружной оболочки заполнены целиком. Криптоном заканчивается IV период Периодической системы. Подобные рассуждения применимы и к остальным элементам таблицы Менделеева, однако эти данные можно найти в справочниках. Отметим лишь, что и начальные элементы последующих периодов Rb, Cs, Fr являются щелочными металлами, а их последний электрон находится в s -состоянии. Кроме того, атомы инертных газов (Не, Ne, Ar, Кr, Хе, Rn) занимают в таблице особое положение — в каждом из них s - и p- состояния наружной оболочки целиком заполнены и ими завершаются очередные периоды Периодической системы.
Таким образом, открытая Менделеевым периодичность в химических свойствах элементов объясняется повторяемостью в структуре внешних оболочек у атомов родственных элементов. Так, инертные газы имеют одинаковые внешние оболочки из 8 электронов (заполненные s- и p -состояния); во внешней оболочке щелочных металлов (Li, Na, К, Rb, Cs, Fr) имеется лишь один s -электрон; во внешней оболочке щелочноземельных металлов (Be, Mg, Ca, Sr, Ba, Ra) имеется два s -электрона; галоиды (F, О, Br, I, At) имеют внешние оболочки, в которых недостает одного электрона до оболочки инертного газа, и т. д.
23. Рентгеновские спектры
Большую роль в выяснении строения атома, а именно распределения электронов по оболочкам, сыграло излучение, открытое в 1895 г. немецким физиком В. Рентгеном (1845—1923) и названное рентгеновским. Самым распространенным источником рентгеновского излучения является рентгеновская трубка, в которой сильно ускоренные электрическим полем электроны бомбардируют анод (металлическая мишень из тяжелых металлов, например W или Pt), испытывая на нем резкое торможение. При этом возникает рентгеновское излучение, представляющее собой электромагнитные волны с длиной волны примерно 10–12—10–8 м. Волновая природа рентгеновского излучения доказана опытами по его дифракции.
Исследование спектрального состава рентгеновского излучения показывает, что его спектр имеет сложную структуру и зависит как от энергии электронов, так и от материала анода. Спектр представляет собой наложение сплошного спектра, ограниченного со стороны коротких длин волн некоторой границей lmin, называемой границей сплошного спектра, и линейчатого спектра — совокупности отдельных линий, появляющихся на фоне сплошного спектра.
Исследования показали, что характер сплошного спектра совершенно не зависит от материала анода, а определяется только энергией бомбардирующих анод электронов. Детальное исследование свойств этого излучения показало, что оно испускается бомбардирующими анод электронами в результате их торможения при взаимодействии с атомами мишени. Сплошной рентгеновский спектр поэтому называют тормозным спектром. Этот вывод находится в согласии с классической теорией излучения, так как при торможении движущихся зарядов должно действительно возникать излучение со сплошным спектром.
Из классической теории, однако, не вытекает существование коротковолновой границы сплошного спектра. Из опытов следует, что чем больше кинетическая энергия электронов, вызывающих тормозное рентгеновское излучение, тем меньше lmin. Это обстоятельство, а также наличие самой границы объясняются квантовой теорией. Очевидно, что предельная энергия кванта соответствует такому случаю торможения, при котором вся кинетическая энергия электрона переходит в энергию кванта, т. е.
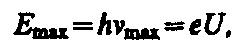
где U—разность потенциалов, за счет которой электрону сообщается энергия Еmax, nmax — частота, соответствующая границе сплошного спектра. Отсюда граничная длина волны
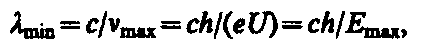
что полностью соответствует экспериментальным данным. Измеряя границу рентгеновского сплошного спектра, по формуле можно определить экспериментальное значение постоянной Планка h, которое наиболее точно совпадает с современными данными.
При достаточно большой энергии бомбардирующих анод электронов на фоне сплошного спектра появляются отдельные резкие линии — линейчатый спектр, определяемый материалом анода и называемый характеристическим рентгеновским спектром (излучением).
По сравнению с оптическими спектрами характеристические рентгеновские спектры элементов совершенно однотипны и состоят из нескольких серий, обозначаемых К, L, М, и O. Каждая серия, в свою очередь, содержит небольшой набор отдельных линий, обозначаемых в порядке убывания длины волны индексами a, b, g,... (Кa, Кb, Кg,.... La, Lb, Lg,...). При переходе от легких элементов к тяжелым структура характеристического спектра не изменяется, лишь весь спектр смещается в сторону коротких волн. Особенность этих спектров заключается в том, что атомы каждого химического элемента, независимо от того, находятся ли они в свободном состоянии или входят в химическое соединение, обладают определенным, присущим только данному элементу линейчатым спектром характеристического излучения. Так, если анод состоит из нескольких элементов, то и характеристическое рентгеновское излучение представляет собой наложение спектров этих элементов.
Рассмотрение структуры и особенностей характеристических рентгеновских спектров приводит к выводу, что их возникновение связано с процессами, происходящими во внутренних, застроенных электронных оболочках атомов, которые имеют сходное строение.
Исследуя рентгеновские спектры элементов, английский физик Г. Мозли (1887—1915) установил в 1913 г. соотношение, называемое законом Мозли:
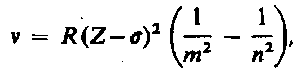
где n — частота, соответствующая данной линии характеристического рентгеновского излучения, R — постоянная Ридберга, s — постоянная экранирования, т = 1, 2, 3,... (определяет рентгеновскую серию), n принимает целочисленные значения начиная с m+1 (определяет отдельную линию соответствующей серии). Закон Мозли подобен обобщенной формуле Бальмера для атома водорода. 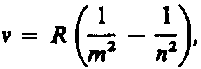
Смысл постоянной экранирования заключается в том, что на электрон, совершающий переход, соответствующий некоторой линии, действует не весь заряд ядра Zе, а заряд (Z–s)e, ослабленный экранирующим действием других электронов. Например, для Ka-линии s = 1, и закон Мозли запишется в виде 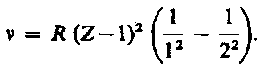
24. Молекулы: химические связи, понятие об энергетических уровнях
Молекула — наименьшая частица вещества, состоящая из одинаковых или различных атомов, соединенных между собой химическими связями, и являющаяся носителем его основных химических и физических свойств. Химические связи обусловлены взаимодействием внешних, валентных электронов атомов. Наиболее часто в молекулах встречается два типа связи: ионная и ковалентная.
Ионная связь (например, в молекулах NaCl, KBr) осуществляется электростатическим взаимодействием атомов при переходе электрона одного атома к другому, т. е. при образовании положительного и отрицательного ионов. Ковалентная связь (например, в молекулах H2, С2, СО) осуществляется при обобществлении валентных электронов двумя соседними атомами (спины валентных электронов должны быть антипараллельны). Ковалентная связь объясняется на основе принципа неразличимости тождественных частиц, например электронов в молекуле водорода. Неразличимость частиц приводит к специфическому взаимодействию между ними, называемому обменным взаимодействием. Это чисто квантовый эффект, не имеющий классического объяснения, но его можно себе представить так, что электрон каждого из атомов молекулы водорода проводит некоторое время у ядра другого атома и, следовательно, осуществляется связь обоих атомов, образующих молекулу. При сближении двух водородных атомов до расстояний порядка боровского радиуса возникает их взаимное притяжение и образуется устойчивая молекула водорода.
Молекула является квантовой системой; она описывается уравнением Шредингера, учитывающим движение электронов в молекуле, колебания атомов молекулы, вращение молекулы. Решение этого уравнения — очень сложная задача, которая обычно разбивается на две: для электронов и ядер.
Энергия изолированной молекулы
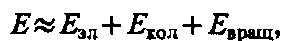 (1)
(1)
где Еэл — энергия движения электронов относительно ядер, Екол — энергия колебаний ядер (в результате которых периодически изменяется относительное положение ядер), Евращ — энергия вращения ядер (в результате которых периодически изменяется ориентация молекулы в пространстве). В формуле (1) не учтены энергия поступательного движения центра масс молекулы и энергия ядер атомов в молекуле. Первая из них не квантуется, поэтому ее изменения не могут привести к возникновению молекулярного спектра, а вторую можно не учитывать, если не рассматривать сверхтонкую структуру спектральных линий. Отношения Еэл: Екол: Евращ = 1: 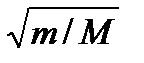 : т/М, где т — масса электрона, М — величина, имеющая порядок массы ядер атомов в молекуле, т/М»10–5¸ 10–3. Поэтому Еэл > > Екол > > Евращ. Доказано, что Еэл»1¸ 10 эВ, Екол»10–2¸ 10–1 эВ, Евращ»10–5¸ 10–3 эВ.
: т/М, где т — масса электрона, М — величина, имеющая порядок массы ядер атомов в молекуле, т/М»10–5¸ 10–3. Поэтому Еэл > > Екол > > Евращ. Доказано, что Еэл»1¸ 10 эВ, Екол»10–2¸ 10–1 эВ, Евращ»10–5¸ 10–3 эВ.
Каждая из входящих в выражение (1) энергий квантуется (ей соответствует набор дискретных уровней энергии) и определяется квантовыми числами. При переходе из одного энергетического состояния в другое поглощается или испускается энергия DE=hn. При таких переходах одновременно изменяются энергия движения электронов, энергии колебаний н вращения. Из теории и эксперимента следует, что расстояние между вращательными уровнями энергии DEвращ гораздо меньше расстояния между колебательными уровнями DEкол которое, в свою очередь, меньше расстояния между электронными уровнями DEэл.