Примеры типовых макроэкономических моделей

Экономико-математические модели и принятие решений

Модель межотраслевого баланса (модель В. Леонтьева). Каждая из n отраслей производит свой (обобщенный) продукт. Выпуск распределяется в заданной пропорции между конечным потреблением, другими отраслями и внутренними потребностями отрасли. Кроме того, описывается прирост производственных мощностей. Модель описывается уравнениями:

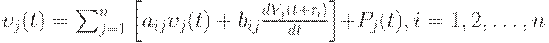
где 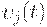- поток выпуска продукта 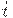в момент времени 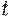(единица измерения = единица продукта / единица времени);

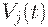- мощность 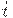- го производства или максимальный выпуск;

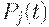- поток конечного (непроизводственного) потребления;

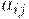- коэффициенты прямых сырьевых затрат (количество продукта 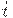, необходимое для производства продукта );

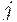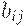- количество фондообразующего продукта 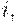идущее на единичный прирост мощности в отрасли ;

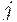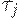- продолжительность строительства мощности в отрасли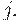

Таким образом, выпуск 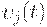расходуется на покрытие сырьевых и фондообразующих затрат и конечное потребление.

Эконометрические модели народного хозяйства (типа Брукингской и Уортоновской). В основе этих моделей лежат: 1) балансовые соотношения; 2) функциональные зависимости - производственная функция и функция потребительского спроса.

Производственная функция 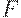задает зависимость национального дохода 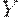от стоимости основных фондов (капитала) 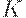и от используемых трудовых ресурсов :

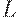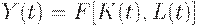
Функция спроса 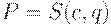задает зависимость вектора 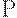конечного потребления, т.е. набора потребляемых товаров, от вектора с цен на эти товары и дохода .

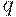Паутинообразные модели имеют дело с динамикой спроса и предложения. Пусть 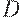- спрос, 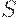- предложение, 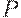- цена, 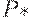- равновесная цена, 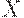- объем производства, 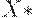- равновесный объем производства. Равновесные 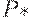и 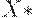находят из условия совпадения спроса и предложения .

Однако более реалистичной является гипотеза запаздывания предложения. Например, пусть при цене в прошлый период 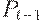объем предложения в данный период есть 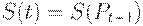. Считаем, что цена 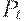устанавливается на рынке так, чтобы был куплен весь объем выпущенной продукции 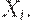Следовательно,

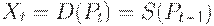
Пусть спрос и предложение достаточно точно описываются линейными функциями от цены

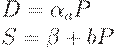
Такое предположение вполне естественно, если в модели рассматривается окрестность точки равновесия, а функции спроса и предложения гладкие. Тогда

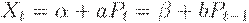
(1)

Равновесие наступает, когда

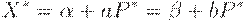
(2)

Вычитая (1) из (2), получаем, что

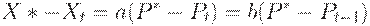
(3)

Обозначим 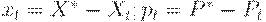- отклонения от равновесия. Из (3) получим 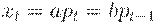, откуда 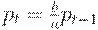Решение этого уравнения имеет вид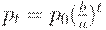

В зависимости от того, чему равно 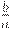, получим либо затухающие колебания 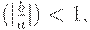сходящиеся к 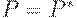и 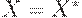, либо колебания c возрастающей амплитудой 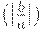. В промежуточном случае 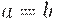амплитуда колебаний постоянна.

Тот же результат справедлив и в модели с непрерывным временем. Будем считать, что спрос меняется не только в зависимости от цены, но и в зависимости от ее динамики, т.е.

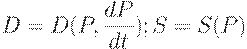
Тогда аналогом (13.1) является уравнение 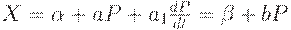, решением которого является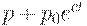

В рассматриваемых моделях считалось, что производители ожидают, что цена останется, как в предшествующий период (и устанавливают объем изготавливаемого товара исходя из этих ожиданий). Модель может быть усовершенствована. Для установления объема изготавливаемого товара производителям более реалистично считать, что в момент времени 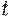цена на товар будет равна , где 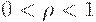, т.е. цена изменится в направлении, обратном тому, в котором она изменялась в прошлый период. Тогда 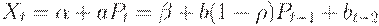, следовательно,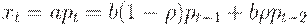

Дальнейшее развитие модели состоит во введении в нее запасов. Ожидая повышения цен, продавцы создают запасы товара.

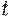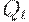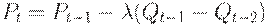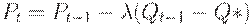Запасы в момент времени обозначим . Тогда изменение запасов за период времени от t-1 до t есть . В модели цену можно устанавливать различными способами, например, или , где 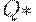- запасы в точке равновесия. В первом случае получим 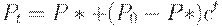, где 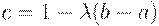, а во втором - .

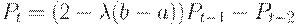Модель экономического цикла. Сначала рассмотрим простую модель без учета запаздывания, а также без учета экспорта-импорта, налогов и государственных расходов.

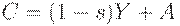
	(4)
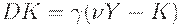
	(5)

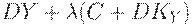
(6)

где 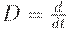- символ операции дифференцирования; 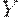- реальный чистый доход, - реальное потребление, 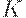- объем основного капитала, 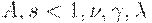- положительные константы. Более точно, 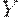- сумма всех видов конечных доходов, полученных в народном хозяйстве, деленная на индекс инфляции (т.е. реальный валовой национальный продукт за вычетом затрат на возмещение основного капитала); - общие затраты на потребительские товары конечных покупателей в народном хозяйстве, деленные на индекс инфляции; K - объем основного капитала всего народного хозяйства (в сопоставимых ценах).

Уравнение (4) вытекает из теории Кейнса, а именно, из соотношения: потребление = национальный доход - сбережения + автономное потребление. Значит, 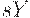- часть дохода, идущая на сбережения, 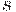- предельная склонность к сбережениям, 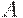- автономное потребление (та доля потребления, которая не зависит от дохода, своеобразный прожиточный минимум).

Уравнение (5) допускает несколько интерпретаций. Рассмотрим две из них.

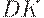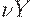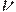1. В первой интерпретации - это норма капитальных вложений в основной капитал. Допустим, существует оптимальный объем основного капитала и он равен некоторой доле от национального дохода - , где - оптимальное соотношение " капитал-выпуск". Тогда уравнение (5) означает, что норма капитальных вложений в основной капитал пропорциональна превышению оптимального объема основного капитала над действительным.

2. Основное соотношение, описывающее капитальные вложения, имеет вид:

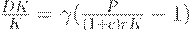
(7)

где P - реальная прибыль, 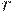- норма процента, 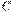- премия за риск. Из соотношения (7) легко получить (5).

В уравнении (6) 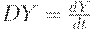- рост производства (поскольку все производство = всему доходу = 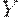). Рост производства зависит от избытка спроса. Потребление (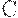) + накопление (оно превращается в капитальные вложения 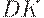) - чистый национальный доход (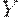) - это и есть избыток спроса (то, что потребляется и накопляется, может быть не равно чистому доходу).

Для равновесной системы все производные по времени равны 0. Равновесные значения и 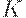таковы:

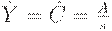
	(8)
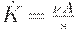
	(9)

Этот результат не предназначен для непосредственного практического использования, т.к. в модели не учитываются ограничения на выпуск, накладываемые рабочей силой и объемом основного капитала. Однако он нужен, чтобы найти отклонения от равновесия 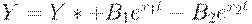- решение системы (4)-(5)-(6)-(8)-(9), где 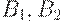зависят от 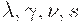. В зависимости от 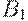и 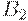получим согласно теории линейных дифференциальных уравнений следующие четыре варианта траекторий 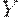: 1) незатухающие колебания (экономические циклы); 2) затухающие колебания; 3) взрывоподобные колебания; 4) взрывоподобная, но не колебательная траектория.

Довольно часто в экономике реально осуществляется приближение к первому варианту - экономические циклы.

Усложним модель, введем запаздывание. В модели (4)-(6) предполагается мгновенная реакция потребления на изменение дохода. На самом деле это неверно. Вместо уравнения (4) напишем

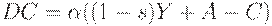
(10)

где 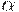- параметр, определяющий быстродействие системы.

Теперь добавим запасы. Вместо уравнения (6) получим

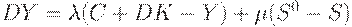
	(11)
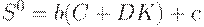
	(12)

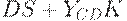
(13)

где 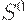- оптимальный уровень запасов, равен некоторой постоянной величине + часть потребления и капитальных вложений, 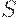- фактический уровень запасов. Уравнение (11) отражает тот факт, что рост производства зависит от избытка спроса и от превышения оптимальных запасов над фактическими. (Уравнения (10) и (11) аналогичны соответствующим соотношениям для паутинообразных моделей.)

Добавим в систему экспорт-импорт, налоги и государственные расходы. Теперь с учетом (11)-(13) получим модель в виде системы уравнений

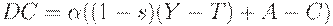
	(14)
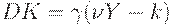
	(15)

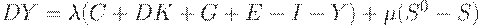
	(16)
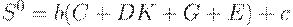
	(17)

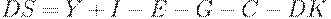
	(18)
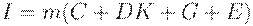
	(19)

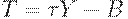
(20)

где 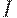- реальный импорт, 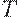- реальный объем налогов за вычетом государственных трансфертных платежей, 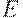- реальный экспорт, 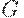- реальные государственные расходы на товары и услуги.

В уравнении (14) национальный доход, идущий на потребление и накопление, уменьшился на сумму налогов, т.е. по сравнению с (10) произошла замена .

Далее заметим, что теперь - общее потребление товаров как отечественного, так и импортного производства, а 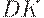теперь есть рост основного капитала частного сектора. Накопление основного капитала частного сектора входит в .

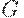Уравнение (16) отличается от (11) на величину 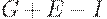, т.к. 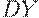- рост производства зависит от избытка спроса, который теперь равен тому, что общество расходует (т.е. потребляет () + вкладывает (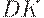) + экспорт (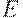) + государственные расходы (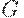)) за вычетом того, что общество получает (национальный доход (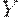) + импорт ()).

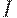Уравнение (17) предполагает, что желаемый уровень запасов есть линейная функция валового сбыта, а валовой сбыт это: 1) сбыт потребительских товаров отдельным потребителям ; 2) сбыт капитальных благ фирмам (капитальные вложения) 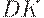; 3) сбыт товаров в государственном секторе 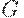; 4) сбыт иностранным производителям .

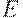Уравнение (18) означает, что изменение запасов равно всем товарам 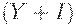минус весь сбыт .

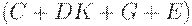Уравнение (19) предполагает, что импорт - это доля всего сбыта.

Уравнение (20) предполагает, что налоги - линейная функция доходов, тогда 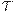- аналог процентной ставки. То, что в уравнении имеется отрицательная константа 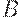, говорит о том, что - возрастающая функция, т.е. чем больше доход, тем больше налог.

При решении системы (14)-(20) выяснилось, в частности, что введение налогов и импорта оказывает на экономику стабилизирующее воздействие.

Модель экономического роста. В этой модели, в отличие от модели экономического цикла, считается, что предложение денег пропорционально 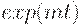, и предложение труда пропорционально , т.е явно учитываются процессы инфляции и изменение численности необходимой рабочей силы, причем и в том, и в другом случае предполагается экспоненциальный рост.

Без учета бюджетной политики модель выглядит так:

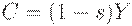
	(21)
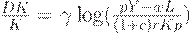
	(22)

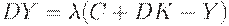
	(23)
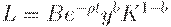
	(24)

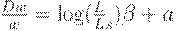
	(25)
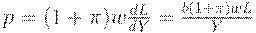
	(26)

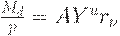
	(27)
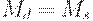
	(28)

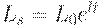
	(29)
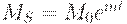
	(30)

где 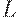- численность используемой рабочей силы;

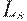- предложение труда;

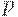- уровень цен;

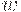- ставка заработной платы;

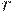- норма процента;

- спрос на деньги;

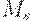- предложение денег;

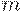- темп роста предложения денег;

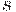- склонность к сбережениям.

Остальные переменные определены выше при рассмотрении модели экономического цикла.

Уравнение (21) означает, что " доход = сбережение + потребление". Уравнение (22) - формула для нормы прироста основного капитала, аналогичная (7). Уравнение (23) означает, что рост производства равен избытку спроса. Уравнение (24) отражает тот факт, что количество рабочей силы, требуемой для выпуска одного и того же количества продукции, все время убывает благодаря НТР. Таким образом, это уравнение учитывает технический прогресс. Уравнение (25) описывает изменение цен на рынке труда. Уравнение (26) утверждает, что уровень цен равен предельным издержкам (издержки на рабочую силу 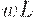, предельные издержки 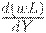) плюс некоторая добавка. В уравнении (27) - те активы, которые население желает держать в денежной форме. Реальный спрос на деньги 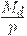тем выше, чем выше доход 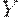и ниже норма процента r. Уравнение (28) означает, что спрос на деньги равен предложению денег. Это возможно, если считать, что норма процента все время подстраивается так, чтобы выполнялось это равенство. В уравнении (29) зафиксировано, что предложение труда растет со временем. В уравнении (30) предполагается, что предложение денег растет со временем.

При решении этой системы выяснилось, что, как и раньше, чем больше 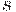, тем стабильнее 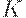и 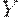, но в отличие от модели экономического цикла, равновесные 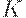и 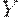теперь растут при увеличении 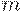- темпа роста и предложения денег.

Теперь отразим в модели экономическое регулирование. Существование денежной политики можно выразить заменой уравнения (30) на

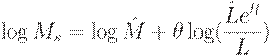
(31)

где 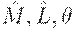- положительные константы, 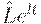- оптимальная траектория занятости, 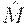- оптимальное предложение денег при оптимальном уровне занятости.

Чтобы отразить существование государственных расходов и налогов, изменим в системе уравнений (21)-(29), (31) значения некоторых переменных:

C- личное потребление и государственные расходы;

K- сумма государственного и частного основного капитала;

sY- сумма частных и государственных сбережений.

Государственные сбережения - это налоги минус государственные расходы, поэтому, чтобы отразить налоги, сделаем s переменной величиной:

(32)

где 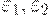- параметры бюджетной политики. В параметре s учитывается: 1) отношение личного потребления к личному доходу; 2) отношение поступлений от налогов к доходу; 3) отношение текущих государственных расходов к поступлениям от налогов. Все это можно учесть с помощью параметров 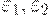\theta, которые являются управляющими.

Модель межотраслевых взаимодействий. Рассмотрим типичную макроэкономическую модель открытого типа (незамкнутую) - модель межотраслевых взаимодействий. Ее формируют две группы математических зависимостей: 1) система уравнений - баланс объема производства каждого вида продукции и его распределение между потребителями (другими производителями и конечными потребителями); 2) система неравенств, которые описывают зависимость между производственными возможностями каждой отрасли и ограничивающими наличными ресурсами (основные фонды и живой труд).

В эту модель нужно ввести извне вектор 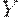- конечный продукт и учесть его деление на потребление, накопление, экспорт, государственные резервы, налоги. Далее, следует задать вектор 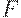- производственные фонды и вектор 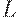- ресурсы живого труда. Это означает, что " вокруг" модели межотраслевых взаимодействий необходимо построить модель доходов и потребления населения - для определения 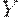, модель формирования национального дохода - для определения 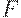, модель " демография - трудовые ресурсы" для определения 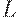и.т.п., то есть создать т.н. макромодельный комплекс.

Макроэкономические модели можно условно разделить на два вида. Одни из них описывают, как сказать, типовую страну, без привязки к ее конкретным особенностям. Другие предназначены для использования в конкретных условиях, описывают вполне определенную экономическую реальность. Рассмотрим модели экономики отдельных стран и мирового хозяйства в целом.

Модель влияния государственной финансовой политики на экономику США. В эту модель входят всего 6 переменных, она подходит для аналитического анализа и иллюстрации влияния правительственного фонда заработной платы, правительственного заказа, налога на деловую активность, на личное потребление, заработную плату частного сектора, прибыли, инвестиции, основной капитал и национальных доход.

В рассматриваемой модели переменные управления таковы:

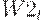- правительственный фонд заработной платы на 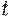-м отрезке времени;

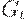- правительственные заказы на 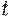-м отрезке времени;

- налог на деловую активность.

Используются эндогенные (заданные извне) переменные:

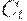- потребление на 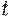-м отрезке времени,

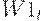- фонд заработной платы в частном секторе на 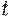-м отрезке времени,

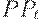- прибыли на 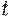-м отрезке времени,

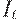- инвестиции на 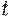-м отрезке времени,

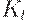- основной капитал в конце 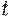-го отрезка времени,

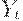- национальный доход на 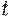-м отрезке времени.

В модель входят уравнения функционирования и тождества. Уравнения функционирования касаются потребления:

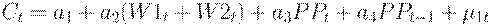
инвестиций:

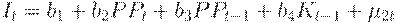
и спроса на рабочую силу:

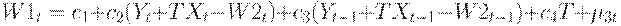
где - случайные возмущения.

Тождества имеют смысл балансовых соотношений (законов сохранения):

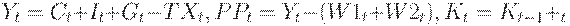
Таким образом, в уравнении потребления зафиксировано, что потребление зависит от заработной платы в частном и государственном секторах, от прибыли в настоящий и предшествующий период времени. В уравнении инвестиций принято, что инвестиции зависят от прибылей в настоящий и предшествующий периоды времени и от основного капитала в предшествующий период времени. Спрос на рабочую силу фактически зависит от прибыльности в настоящий и предшествующий периоды времени.

Коэффициенты в уравнениях и тождествах определяются путем анализа конкретных экономико-статистических данных эконометрическими методами.

Модель экономики США. Существует множество моделей экономики США. Рассмотрим сначала т.н. Уортонскую модель (фактически макромодельный комплекс). Эта модель содержит 734 соотношения, из них 292 уравнения поведения и 442 тождества. Модель состоит из 8 блоков:

1. конечный спрос;

2. межотраслевые потоки;

3. потребность в трудовых ресурсах;

4. заработная плата;

5. цены производства;

6. цены конечного потребления;

7. прочие доходы;

8. финансы.

Используемые в модели сценарии состоят в том или ином изменении

1. федеральных закупок товаров;

2. закупок товаров и услуг органами штатов и местного управления;

3. трансфертных платежей;

4. экспорта;

5. налога на инвестиции.

Управляющими параметрами были следующие:

1. статьи расходов государственного бюджета;

2. ставки налогов;

3. цены и заработная плата;

4. курс доллара;

5. импортные пошлины.

Цель модели - оценка эффективности деятельности федерального правительства. Упрощенная схема этой модели была приведена выше.

Рассмотрим более простую, нежели Уортонская, модель, содержащую гораздо меньше уравнений, однако хорошо иллюстрирующую принципы построения моделей рассматриваемого типа.

Сначала выделяются блоки, из которых будет состоять модель, затем перечисляются переменные, которые входят в модель (их 35). Формируется таблица объясняемых переменных и объясняющих факторов. На основании этой таблицы строится система уравнений. Например, по таблице находим, что основной капитал 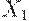зависит от:

1. основного капитала в предшествующий период времени ;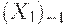

2. инвестиций производственного назначения в предшествующий момент времени ;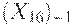

3. краткосрочного процента в предшествующий момент времени ;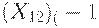

4. возмещения выбытия фондов ;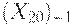

5. занятости в частном секторе .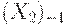

Теперь строим линейное регрессионное уравнение с авторегрессионным членом:

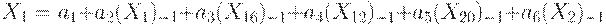
Сложный вопрос состоит в выборе тех переменных, от которых зависит 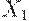. Он решается с помощью того или иного алгоритма нахождения " информативного подмножества переменных" в регрессионном анализе. Используются парные и множественные коэффициенты линейной или непараметрической корреляции.

Модель мирового хозяйства. Рассмотрим проект ЛИНК, который разработан в 1970-х годах Уортонской ассоциацией эконометрических прогнозов под руководством нобелевского лауреата по экономике Л.Клейна.

Макромодельный комплекс ЛИНК - совокупность разрабатываемых независимо друг от друга, различных по размерам и структуре эконометрических моделей национальной экономики ряда стран и регионов, которые увязываются в единую систему посредством субмодели мировой торговли.

В систему ЛИНК включены:

1. модель экономики США - 207 уравнений;

2. модель экономики Канады - 183 уравнения;

3. модель экономики Франции - 32 уравнения;

4. модель экономики ФРГ - 137 уравнений;

5. и.т.д. (модели национальных экономик Великобритании, Италии, Швеции, Финляндии, Бельгии, Нидерландов, Австрии, Японии, Австралии);

6. единая модель экономики развивающихся стран;

7. единая модель экономики социалистических стран;

8. единая модель экономики стран остального мира.

Модель для каждой страны (группы стран) разрабатывалась независимо. Сначала модели опробовались для каждой страны (группы стран) отдельно. Потом все эти модели объединялись в мировую модель посредством модели мировой торговли.

Модели развитых стран содержали блоки:

1. блок производства;

2. блок потребления;

3. блок инвестиций;

4. блок доходов и занятости;

5. блок цен;

6. блок денежного обращения;

7. блок внешней торговли.

Каждая страна описывалась с помощью моделей верхнего и нижнего уровня.

Верхний уровень состоит из вышеперечисленных блоков. Далее каждый блок раскрывается. Например, в блок денежного обращения включены параметры: 6.1) количество денег в обращении; 6.2) дефицит бюджета; 6.3) сальдо платежного баланса; 6.4) индекс цен (дефлятор ВНП); 6.5) индекс розничных цен; 6.6) индекс оптовых цен; 6.7) учетная ставка по долгосрочным кредитам; 6.8) учетная ставка по краткосрочным кредитам. Модели верхнего уровня содержат взаимосвязи между этими параметрами.

Нижний уровень модельного комплекса содержит детализированные модели, описывающие регионально-страновые и проблемно-функциональные отношения.

С помощью системы ЛИНК были выявлены нетривиальные экономические связи. Например, оказалось, что снижение налогов в США приводит к улучшению платежного баланса Франции.

Модель мировой торговли. Рассмотрим моделирование товарных потоков между парами стран. Для этого используются, например, гравитационные методы, приводящие к соотношениям:

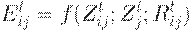
где 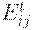- экспорт из страны i в страну j в интервал времени t;

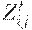- факторы, определяющие потенциальное предложение экспорта страной 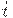для страны 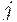в интервал времени ;

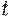- факторы, определяющие потенциальный спрос страны 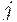на импорт в интервал времени ;

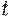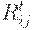- факторы, относящиеся к продвижению товарного потока из страны 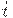в страну 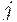в интервал времени t.

С помощью этой и других моделей независимо разработанные модели отдельных стран можно увязать в единую мировую макромодель.

Вопросам построения, изучения и использования макроэкономических моделей при разработке и принятии управленческих решений посвящена огромная литература.

В системы поддержки принятия решений входят не только общие макроэкономические модели, но и модели, касающиеся отдельных сторон функционирования народного хозяйства, в частности, модели налогообложения.

Модель вычетов при налогообложении прибыли. Математические модели налогообложения, используемые в зарубежных странах, весьма разнообразны. Начнем с канадской модели Т2. Она посвящена моделированию изменения нормы вычетов из налоговых обязательств затрат капитальных активов (при уплате налогов на прибыль). Предполагается, что каждая фирма самостоятельно проводит максимизацию скидок и минимизацию налоговых сборов (в рамках действующего налогового законодательства).

Анализируются изменения в первый год после управляющего воздействия и в " зрелой" системе через большой промежуток времени. Любопытно, что управляющим воздействием является не изменение ставки налога, а изменение правил расчета амортизационных начислений, причем это изменение касается лишь вновь приобретаемых единиц основных фондов (поэтому новые ставки амортизации лишь постепенно распространяются на налоговую базу).

В модели " зрелой" системы налогообложения используются такие параметры, как:

· средняя прошлая норма прироста капитала,

· показатель экспоненциальной амортизации,

· индекс цен капитала (учитывающий, например, рост во времени стоимости участков земли в неизменных ценах),

· средний коэффициент (индекс) инфляции (для народного хозяйства в целом),

· норма вычетов из налоговой базы затрат капитальных активов.

Моделируется также влияние на налоговые поступления изменения ставки зачета налога на инвестиции.

Модель построена на основе анализа данных, приведенных в выборке налоговых деклараций 15000 фирм (из 760000 фирм Канады).

Модели поступлений от налога на добавленную стоимость. В Румынии и Венгрии для оценки суммарных поступлений от налога на добавленную стоимость сначала оценивают налоговую базу на основе макроэкономических показателей. Считают, что она равна:

(валовой внутренний продукт) + (импорт) - (экспорт) - (фиксированные капиталовложения) - (изменение запасов) - (добавленная стоимость по освобожденным от налога секторам) - (оценка НДС для малого бизнеса и строительства частного жилья (до 1992 г.)).

Прогноз на следующий год осуществляется умножением налоговой базы предыдущего года на коэффициент, равный сумме прогнозов индекса инфляции и экономического роста за следующий год.

Действительная ставка налоговых поступлений от НДС рассчитывается путем деления объема чистых поступлений на налоговую базу. Для целей прогноза налоговая ставка считается постоянной (либо прогнозируется с помощью теории временных рядов).

Прогноз объема налоговых поступлений получают перемножением прогнозов объема налоговой базы и прогноза действительной ставки поступлений от НДС.

В Венгрии в Министерстве финансов разработана модель налоговой базы и поступлений от налога на добавленную стоимость на основе межотраслевой модели " вход-выход" (21 отрасль).

Модель подоходного налога в Великобритании построена на основе репрезентативной выборки, включающей 80000 налогоплательщиков (физических лиц) из 25 миллионов плательщиков подоходного налога. Используются данные налоговых деклараций.

С использованием соображений демографии, социологии, медицинской статистики и макроэкономики прогнозируется изменение налоговой базы, при этом структура модели определяется экспертами из представителей перечисленных наук, а коэффициенты оцениваются по выборочным данным.

Знание налоговой базы позволяет прогнозировать первоначальное (в первый год) изменение налоговых сборов при применении управляющих воздействий. Для оценки дальнейшей динамики необходимо учитывать реакцию налогоплательщиков на изменение системы налогообложения (в первом приближении - линейный отклик с коэффициентами эластичности в качестве множителей перед приращениями переменных). Прогнозирование на далекую перспективу возможно лишь методом сценариев, поскольку необходимо спрогнозировать, в частности, динамику народонаселения.

Моделирование процессов налогообложения в России Разработка имитационных моделей процессов налогообложения с целью оценки влияния управляющих воздействий на эти процессы, сбора и обобщения информации о процессах налогообложения на основе компьютерных систем представляет собой достаточно наукоемкую и трудоемкую задачу. Основные задачи, которые необходимо решить при разработке подобной модели, таковы:

· анализ нормативной базы и практической реализации процессов налогообложения,

· постановка основных задач оценки управляющих воздействий на процессы налогообложения,

· разработка и изучение системы математических моделей, имитирующих процессы налогообложения в реально действующей налоговой системе,

· решение тех же задач для будущей, модифицированной согласно решениям государственной власти, налоговой системы;

· разработка диалоговой компьютерной системы и соответствующих программных средств, позволяющих сотрудникам налоговых служб решать стоящие перед ними задачи оценки управляющих воздействий на процессы налогообложения.

Целесообразна разработка моделей для анализа предлагаемых различными организациями и лицами налоговых систем, а также для оценки влияния процессов налогообложения на статику и динамику микро- и макроэкономических характеристик.

Сформулируем основные требования к выполнению подобного исследования в российских условиях:

· работа должна основываться на анализе действующей системы сбора налогов и других обязательных платежей в бюджетную систему Российской Федерации (в федеральный бюджет и в бюджеты территорий),

· математические модели и соответствующие компьютерные разработки, предназначенные для оценки управляющих воздействий на процессы налогообложения, должны позволять рассчитывать объемы налоговых поступлений при тех или иных значениях управляющих воздействий - ставок налогов, льгот, штрафов,

· они должны предоставлять возможности для анализа модификаций налоговой системы (в частности, путем изменения ставок, системы льгот и штрафов, правил относительно времени внесения платежей, а также введения новых видов налогов),

· конечный программный продукт должен предназначаться для эксплуатации специалистами государственной налоговой службы, не имеющими специальных знаний в программировании и математическом моделировании.

Проблемам моделирования процессов налогообложения в России посвящена монография [13.10]. Рассмотрим один конкретный подход к моделированию процессов налогообложения.

Основные идеи метода компьютерного моделирования ЖОК. Различные субъекты и факторы экономической жизни постоянно влияют друг на друга. Как правило, для каждого из рассматриваемых экономических субъектов (и факторов) можно выделить " непосредственное окружение", которое оказывает влияние на него в конкретный момент. Как правило, на него же этот субъект оказывает некоторое обратное влияние. Дальше начинается самое интересное - волны влияний, порожденные разными субъектами, распространяются по всей совокупности, частично усиливают друг друга, частично погашают, порождая в каждый момент времени новые волны.

Разработан компьютерный метод, называемый далее ЖОК, предназначенный для оценки результатов влияния описывающих ситуацию факторов на итоговые показатели и друг на друга. Метод ЖОК позволяет получать выводы, полезные для управления различными экономическими структурами на микро- и макроуровнях, от бригад и предприятий до государства в целом. Этот метод использует экономико-математическую модель многомерного временного ряда, в которой коэффициенты непосредственного влияния факторов друг на друга и начальные условия задаются экспертами, т.е. представляет собой синтез экспертных и экономико-математических методов. Опишем основные составляющие этого метода.

Сначала экспертным путем определяется список факторов, которые необходимо учитывать при анализе конкретной ситуации. В качестве примера рассмотрим здесь типовое промышленное предприятие. Для него такими факторами являются, на наш взгляд, устойчивость развития, уровень рентабельности, оценка состояния основных и оборотных фондов, положение на рынке, кадровый потенциал, финансовое положение, технологический уровень, технический уровень и качество продукции, степень учета экологических требований, уровень сертификации, научно-технический потенциал и степень его использования, положение в социальной сфере, развитость профсоюзного движения, оценка отношений с конкурентами и властями, и т.д. Основная часть перечисленных факторов носит качественный характер.

Далее определяются необходимые для работы модели начальные уровни факторов, соответствующие современному (т.е. начальному) состоянию изучаемого экономического объекта (проводится оцифровка нечисловых переменных). Они оцениваются экспертами на шкале от (-1) до (+1) с шагом 0, 1. В методе ЖОК степень привлечения экспертов может быть различна - от использования одного эксперта, хорошо знающего ситуацию и на основе своих знаний и интуиции указывающего необходимые параметры и связи, до подключения к работе комиссии экспертов, коллективно оценивающих указанные параметры и связи, с использованием той или иной схемы сбора и анализа экспертных мнений.

Затем экспертами составляется блок-схема непосредственных влияний факторов друг на друга и оценивается степень непосредственных влияний с помощью такой же шкалы от (-1) до (+1) с шагом 0, 1. Получается экономико- математическая модель в виде взвешенного ориентированного графа с начальными данными в вершинах. Она несколько напоминает хорошо известную экономистам схему межотраслевого баланса В. Леонтьева, но в отличие от нее использует не только количественные, но - в основном - качественные факторы. Затем просчитываются итерации (опосредованные влияния второго, третьего и т.д. уровней, соответствующие второму, третьему и т.д. моментам времени) вплоть до получения стабильного состояния. Результат работы модели - конечные уровни факторов.

Модель позволяет просчитать развитие экономической структуры при различных сценариях. Обычно одновременно используют три типа сценариев - " Прогноз", " Поиск " и " Оптимизация ".

Сценарий " Прогноз" показывает результат при отсутствии управляющих воздействий. Он демонстрирует, как будет развиваться ситуация, если в нее не вмешиваться. Исходные данные для сценария " Прогноз" - начальные значения факторов и матрица непосредственных взаимовлияний факторов.

В сценариях типа " Поиск " вводится новое понятие - управляющие факторы. В сценариях этого типа анализируются результаты изменений при наличии тех или иных конкретных воздействий на управляющие факторы. Обычно специалист, работающий с системой ЖОК, имеет целью увеличение значений тех или иных факторов при " удержании" некоторых иных в заданных пределах. В сценариях типа " Поиск " осуществляется эвристический процесс оптимизации, а также анализ поведения системы при тех или иных воздействиях на начальные значения факторов.

В сценариях типа " Оптимизация " кроме списка управляющих факторов задаются целевые факторы и условия на них, которых необходимо добиться. Обычно это - условия выхода на определенные уровни, например, рентабельность должна быть не менее 0.5, а социальная напряженность - не более 0.3. С помощью оптимизационных алгоритмов находится наилучшее управление, позволяющее достигнуть цели или максимально к ней приблизиться. Однако найденные компьютером рекомендации могут включать слишком резкие изменения тех или иных начальных параметров, поэтому результаты расчетов скорее указывают на перспективные варианты изменения управляющих параметров, чем непосредственно задают план действий. С помощью сценариев типа " Поиск " можно на основе этих результатов найти практически реализуемые рекомендации.

Система ЖОК позволяет проследить динамику изменения значений факторов вплоть до их стабилизации, которая обычно наступает через 15-25 итераций (интервалов времени). Такая быстрая сходимость вначале кажется неожиданной. Возможно, сам факт стабилизации является самым важным методологическим выводом из экспериментов с моделью ЖОК: " После первоначальных всплесков замкнутая экономическая система стабилизируется, хотя бы и на весьма низком уровне производства и потребления".

При этом с помощью оцененных экспертами коэффициентов важности факторов (с учетом знака) можно отслеживать общую оценку экономической ситуации.

Система ЖОК является человеко-машинной. Для эффективной работы специалиста желательно, чтобы общее число факторов, используемых в конкретной модели, не превышало 20, а число непосредственных взаимосвязей - 40, хотя эти ограничения несущественны для математического обеспечения компьютерной системы ЖОК. Они существенны для наглядности при построении, обсуждении и совершенствовании модели, для того, чтобы факторы и связи между ними можно было изобразить на листе бумаги или экране компьютера в виде блок-схемы.

Система ЖОК с успехом использовалась для анализа ряда конкретных экономических ситуаций. Так, по заказу Минфина РФ она применялась для анализа взаимовлияний факторов, определяющих динамику налогооблагаемой базы и сбора подоходного налога с физических лиц, налога на имущество, налогов и сборов за пользование природными ресурсами и др. Построенная серия эконометрических моделей обладала некоторыми общими чертами. Прогноз, исходящий из экономического положения 1999 г., во всех случаях указывал на дальнейшее ухудшение ситуации. Активное вмешательство государства в экономику приводило к значительному улучшению показателей, в то время как управление с помощью чисто экономических (монетаристских) методов не позволяло улучшить исходное положение. Полученные результаты подтверждают известную концепцию пяти нобелевских лауреатов по экономике (К.Эрроу, В.Леонтьев и др.), разрабатываемую совместно с Отделением экономики Российской академии наук (Д.С. Львов, С.Ю. Глазьев и др.), о необходимости активного регулирования государством экономических процессов

Другие примеры применения системы ЖОК касались оптимизации экономической стороны деятельности промышленного предприятия или организации в иной сфере, экономических взаимоотношений отраслей народного хозяйства, а также макроэкономического моделирования, в ходе которого удалось вскрыть две неточности в основной схеме известной монографии К.Р. Макконнелла и С.Л. Брю " Экономикс: Принципы, проблемы и политика", а затем исправить их, включив дополнительные блоки в соответствующую модель.

Эконометрический метод ЖОК предназначен для широкого применения при анализе экономического состояния и перспектив промышленных предприятий, банков, различных государственных и коммерческих структур.