
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Принятие решений в задачах логистики
|
|
Термин " логистика" происходит от французского слова " loger" (размещение, расквартирование), которое употребляется в военной терминологии для определения движения военных грузов, их складирования и размещения, а также для описания процесса размещения и расквартирования военных подразделений. В настоящее время термин " логистика" широко используется в деловом мире и определяет теорию и практику движения сырья, материалов, комплектующих изделий, производственных, трудовых и финансовых ресурсов, готовой продукции от их источников к потребителям.
ЛОГИСТИКА - наука о планировании, управлении и контроле за движением материальных, информационных и финансовых ресурсов в различных производственно-экономических системах. Предметом логистики является комплексное управление всеми материальными и нематериальными потоками в таких системах. Новизна концепции логистики в области управления промышленными системами состоит во всестороннем подходе к вопросам движения материальных благ в процессе производства и управления. Логистическая система должна охватывать и согласовывать процессы производства, закупок и распределения продукции, а также быть основой при стратегическом планировании и прогнозировании. Итак, логистика - это экономическая дисциплина, занимающаяся оптимальной организацией материальных, финансовых и информационных потоков.
Одна из основных частей логистики - теория управления запасами. Сколько товара держать на складе? Много - будут омертвляться оборотные средства, вложенные в запас. Мало - слишком часто надо будет заниматься получением новых партий товара и нести соответствующие расходы. Значит, надо рассчитать и использовать оптимальный размер запаса. А для этого необходимо построить соответствующую математическую модель.
Управление запасами (другими словами, материально-техническое снабжение) - неотъемлемая часть работы фирм и организаций. Речь идет о запасах сырья, топлива, материалов, инструментов, комплектующих изделий, полуфабрикатов, готовой продукции на промышленном (или сельскохозяйственном) предприятии, о запасах товаров на оптовых базах, складах магазинов, на рабочих местах продавцов, наконец, у потребителей. Запасы постоянно расходуются и пополняются по тем или иным правилам, принятым на предприятии. Оптимизация этих правил, т.е. оптимальное управление запасами, дает большой экономический эффект.
Математическая теория управления запасами является крупной областью экономико-математических исследований, получившей свое развитие, в основном, начиная с пятидесятых годов ХХ века. Предложенная, видимо, еще в 1915 г. Ф.Харрисом классическая модель теории управления запасами, называемая также моделью Вильсона (в связи с тем, что получила известность после публикации работы Р.Г. Вильсона в 1934 г.), является одним из наиболее простых и наглядных примеров применения математического аппарата для принятия решений в экономической области. В то же время формула оптимального размера заказа, полученная в модели Вильсона, широко применяется на различных этапах производства и распределения продукции, поскольку оказывается практически полезной для принятия решений при управлении запасами, в частности, приносящей заметный экономический эффект. Рассмотрим эту модель подробнее.
Классическая модель управления запасами. Пусть 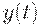 - величина запаса некоторого товара на складе в момент времени
- величина запаса некоторого товара на складе в момент времени 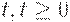 . Дефицит не допускается, т.е.
. Дефицит не допускается, т.е. 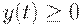 при всех
при всех 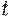 . Товар пользуется равномерным спросом с интенсивностью
. Товар пользуется равномерным спросом с интенсивностью 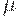 , т.е. за интервал времени
, т.е. за интервал времени 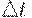 со склада извлекается и поступает потребителям часть запаса величиной
со склада извлекается и поступает потребителям часть запаса величиной 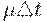 .В моменты времени
.В моменты времени  пополняется запас на складе - приходят поставки величиной
пополняется запас на складе - приходят поставки величиной  соответственно. Таким образом, изменение во времени величины запаса
соответственно. Таким образом, изменение во времени величины запаса 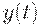 товара на складе изображается зубчатой ломаной линией (рис. 13.1), состоящей из наклонных и вертикальных звеньев, причем наклонные отрезки параллельны.
товара на складе изображается зубчатой ломаной линией (рис. 13.1), состоящей из наклонных и вертикальных звеньев, причем наклонные отрезки параллельны.
Таким образом, в момент t_i величина запаса на складе 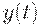 скачком увеличивается на
скачком увеличивается на 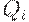 . Следовательно, функция
. Следовательно, функция 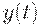 имеет разрывы в точках
имеет разрывы в точках  Для определенности будем считать, что эта функция непрерывна справа.
Для определенности будем считать, что эта функция непрерывна справа.
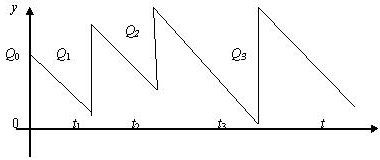
Рис. 13.1. График изменения величины запаса на складе
Пусть 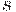 - плата за хранение единицы товара в течение единицы времени. Поскольку можно считать, что величина запаса
- плата за хранение единицы товара в течение единицы времени. Поскольку можно считать, что величина запаса 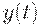 не меняется в течение интервала времени
не меняется в течение интервала времени 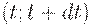 , где
, где 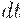 - дифференциал, т.е. бесконечно малая, то плата за хранение всего запаса в течение этого интервала времени равна
- дифференциал, т.е. бесконечно малая, то плата за хранение всего запаса в течение этого интервала времени равна 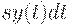 . Следовательно, затраты за хранение в течение интервала времени [0; T), где
. Следовательно, затраты за хранение в течение интервала времени [0; T), где 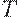 - интервал планирования, пропорциональны (с коэффициентом пропорциональности
- интервал планирования, пропорциональны (с коэффициентом пропорциональности 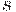 ) площади под графиком уровня запаса на складе
) площади под графиком уровня запаса на складе 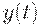 и равны
и равны
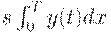
Пусть 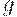 - плата за доставку одной партии товара. Примем для простоты, что она не зависит от размера поставки. Позже покажем, что если эта плата равна
- плата за доставку одной партии товара. Примем для простоты, что она не зависит от размера поставки. Позже покажем, что если эта плата равна  , где
, где 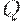 - размер поставки, то оптимальный план поставки - тот же, что и при отсутствии линейного члена. Будет проанализирована и более сложная модель, в которой предусмотрена скидка с ростом поставки, приводящая к выражению
- размер поставки, то оптимальный план поставки - тот же, что и при отсутствии линейного члена. Будет проанализирована и более сложная модель, в которой предусмотрена скидка с ростом поставки, приводящая к выражению 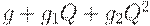 для платы за доставку одной партии товара размером
для платы за доставку одной партии товара размером 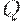 .
.
Пусть 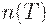 - количество поставок, пришедших в интервале
- количество поставок, пришедших в интервале  . При этом включаем поставку в момент
. При этом включаем поставку в момент 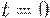 и не включаем поставку в момент
и не включаем поставку в момент 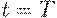 (если такая поставка происходит). Тогда суммарные издержки на доставку товара равны
(если такая поставка происходит). Тогда суммарные издержки на доставку товара равны 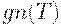 . Следовательно, общие издержки (затраты, расходы) за время
. Следовательно, общие издержки (затраты, расходы) за время 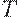 равны
равны
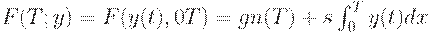
Запись 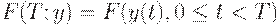 означает, что общие издержки зависят от значений функции
означает, что общие издержки зависят от значений функции 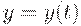 при всех
при всех 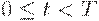 . Символ у обозначает функцию как целое. Другими словами, область определения
. Символ у обозначает функцию как целое. Другими словами, область определения 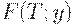 при фиксированном
при фиксированном 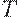 - не множество чисел, а множество функций.
- не множество чисел, а множество функций.
Общие издержки, очевидно, возрастают при росте горизонта планирования  . Поэтому часто используют средние издержки, приходящиеся на единицу времени. Средние издержки за время
. Поэтому часто используют средние издержки, приходящиеся на единицу времени. Средние издержки за время  равны
равны
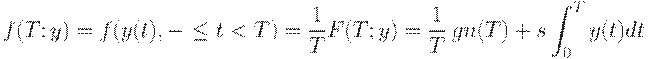
Поскольку товар отпускается со склада с постоянной интенсивностью (скоростью), дефицит не допускается, то доходы от работы склада пропорциональны горизонту планирования, средние доходы постоянны. Следовательно, максимизация прибыли эквивалентна минимизации издержек или средних издержек.
Если задать моменты прихода поставок и величины партий, то будет полностью определена функция 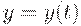 при всех
при всех 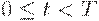 . Верно и обратное - фиксация функции
. Верно и обратное - фиксация функции 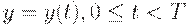 , рассматриваемого вида (рис. 13.1) полностью определяет моменты прихода поставок и величины партий. И то, и другое будем называть планом поставок или планом работы системы управления запасами. Для ее оптимизации необходимо выбрать моменты времени
, рассматриваемого вида (рис. 13.1) полностью определяет моменты прихода поставок и величины партий. И то, и другое будем называть планом поставок или планом работы системы управления запасами. Для ее оптимизации необходимо выбрать моменты времени  пополнения запаса на складе и размеры поставляемых партий товара
пополнения запаса на складе и размеры поставляемых партий товара  так, чтобы минимизировать средние издержки
так, чтобы минимизировать средние издержки 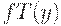 при фиксированном
при фиксированном  . Модель производственной ситуации (т.е. работы склада) описывается четырьмя параметрами -
. Модель производственной ситуации (т.е. работы склада) описывается четырьмя параметрами - 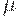 (интенсивность спроса),
(интенсивность спроса), 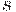 (стоимость хранения единицы продукции в течение единицы времени),
(стоимость хранения единицы продукции в течение единицы времени), 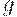 (стоимость доставки партии товара),
(стоимость доставки партии товара),  (горизонт планирования).
(горизонт планирования).
Решение задачи оптимизации. Поставленная задача оптимизации работы склада интересна тем, что неизвестно число 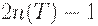 параметров, определяющих план поставок. Поэтому ее решение не может быть проведено с помощью стандартных методов теории оптимизации.
параметров, определяющих план поставок. Поэтому ее решение не может быть проведено с помощью стандартных методов теории оптимизации.
Решим эту задачу в три этапа. На первом установим, что оптимальный план следует искать среди тех планов, у которых все зубцы доходят до оси абсцисс, т.е. запас равен 0 в момент доставки очередной партии. Цель второго этапа - доказать, что все зубцы должны быть одной и той же высоты. Наконец, на третьем находим оптимальный размер поставки.
Оптимальный план. Найдем наилучший план поставок. План, для которого запас равен 0 (т.е. 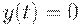 ) в моменты доставок очередных партий, назовем напряженным.
) в моменты доставок очередных партий, назовем напряженным.
Утверждение 1. Для любого плана поставок, не являющегося напряженным, можно указать напряженный план, для которого средние издержки меньше.
Покажем, как можно от произвольного плана перейти к напряженному плану, уменьшив при этом издержки. Пусть с течением времени при приближении к моменту 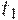 прихода поставки
прихода поставки 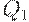 уровень запаса не стремится к 0, а лишь уменьшается до
уровень запаса не стремится к 0, а лишь уменьшается до 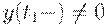 (где знак " минус" означает предел слева функции
(где знак " минус" означает предел слева функции 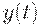 в точке
в точке 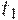 ). Тогда рассмотрим новый план поставок с теми же моментами поставок и их величинами, за исключением величин поставок в моменты
). Тогда рассмотрим новый план поставок с теми же моментами поставок и их величинами, за исключением величин поставок в моменты 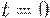 и
и  . А именно, заменим
. А именно, заменим 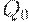 на
на 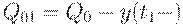 , а
, а 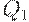 на
на 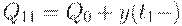 . Тогда график уровня запаса на складе параллельно сдвинется вниз на интервале
. Тогда график уровня запаса на складе параллельно сдвинется вниз на интервале 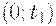 , достигнув 0 в
, достигнув 0 в 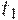 , и не изменится правее точки
, и не изменится правее точки 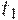 . Следовательно, издержки по доставке партий не изменятся, а издержки по хранению уменьшатся на величину, пропорциональную (с коэффициентом пропорциональности
. Следовательно, издержки по доставке партий не изменятся, а издержки по хранению уменьшатся на величину, пропорциональную (с коэффициентом пропорциональности 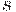 ) площади параллелограмма, образованного прежним и новым положениями графика уровня запаса на интервале
) площади параллелограмма, образованного прежним и новым положениями графика уровня запаса на интервале 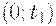 (см. рис. 13.2).
(см. рис. 13.2).
Итак, в результате первого шага перехода получен план, в котором крайний слева зубец достигает оси абсцисс. Следующий шаг проводится аналогично, только момент времени 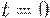 заменяется на
заменяется на  . Если есть такая возможность, второе наклонное звено графика уровня запаса на складе параллельно сдвигается вниз, достигая в крайней правой точке
. Если есть такая возможность, второе наклонное звено графика уровня запаса на складе параллельно сдвигается вниз, достигая в крайней правой точке 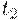 оси абсцисс.
оси абсцисс.
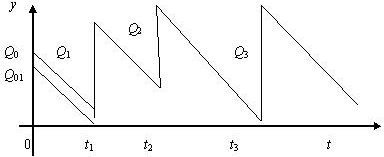
Рис. 13.2. Первый шаг перехода к напряженному плану
Аналогично поступаем со всеми остальными зубцами, двигаясь слева направо. В результате получаем напряженный план. На каждом шагу издержки по хранению либо сокращались, либо оставались прежними (если соответствующее звено графика не опускалось вниз). Следовательно, для полученного в результате описанного преобразования напряженного плана издержки по хранению меньше, чем для исходного плана, либо равны (если исходный план уже являлся напряженным).
Из утверждения 1 следует, что оптимальный план следует искать только среди напряженных планов. Другими словами, план, не являющийся напряженным, не может быть оптимальным.
Утверждение 2. Среди напряженных планов с фиксированным числом поставок минимальные издержки имеет тот, в котором все интервалы между поставками равны.
При фиксированном числе поставок затраты на доставку партий не меняются. Следовательно, достаточно минимизировать затраты на хранение.
Для напряженных планов размеры поставок однозначно определяются с помощью интервалов между поставками:
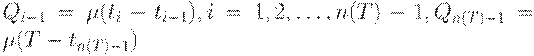
Действительно, очередная поставка величиной 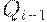 совпадает с размером запаса на складе в момент
совпадает с размером запаса на складе в момент 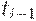 , расходуется с интенсивностью
, расходуется с интенсивностью 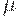 единиц товара в одну единицу времени и полностью исчерпывается к моменту
единиц товара в одну единицу времени и полностью исчерпывается к моменту 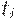 прихода следующей поставки.
прихода следующей поставки.
Для напряженного плана издержки по хранению равны
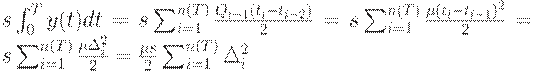
где 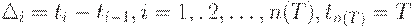 Ясно, что
Ясно, что 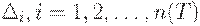 - произвольные неотрицательные числа, в сумме составляющие
- произвольные неотрицательные числа, в сумме составляющие  . Следовательно, для минимизации издержек среди напряженных планов с фиксированным числом поставок достаточно решить задачу оптимизации
. Следовательно, для минимизации издержек среди напряженных планов с фиксированным числом поставок достаточно решить задачу оптимизации
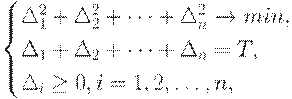
где 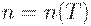
Полученная задача оптимизации формально никак не связана с логистикой, она является чисто математической. Для ее решения целесообразно ввести новые переменные
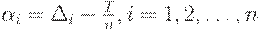
Тогда
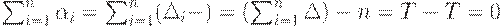
Поскольку
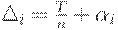 то
то 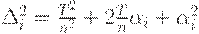 следовательно, с учетом предыдущего равенства имеем
следовательно, с учетом предыдущего равенства имеем
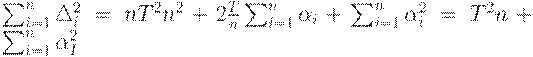
Сумма квадратов всегда неотрицательна. Она достигает минимума, равного 0, когда все переменные равны 0, т.е. при 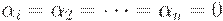 Тогда
Тогда
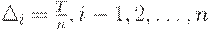
При этих значениях 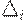 выполнены все ограничения оптимизационной задачи. Итак, утверждение 2 доказано.
выполнены все ограничения оптимизационной задачи. Итак, утверждение 2 доказано.
Для плана с равными интервалами между поставками все партии товара имеют одинаковый объем. Для такого плана издержки по хранению равны
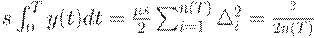
Средние издержки (на единицу времени) таковы:
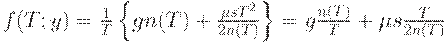
Итак, минимизация средних издержек - это задача дискретной оптимизации. На третьем этапе построения оптимального плана необходимо найти натуральное число 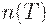 - самое выгодное число поставок.
- самое выгодное число поставок.
Поскольку к моменту  запас товара должен быть израсходован, то общий объем поставок за время
запас товара должен быть израсходован, то общий объем поставок за время 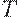 должен совпадать с общим объемом спроса, следовательно, равняться
должен совпадать с общим объемом спроса, следовательно, равняться 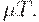 Справедливо балансовое соотношение (аналог закона Ломоносова-Лавуазье сохранения массы при химических реакциях):
Справедливо балансовое соотношение (аналог закона Ломоносова-Лавуазье сохранения массы при химических реакциях):
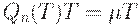
Из балансового соотношения следует, что
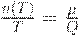
Средние издержки (на единицу времени) можно выразить как функцию размера партии 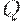 :
:
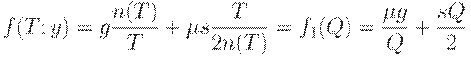
| (33) |
Задача состоит в минимизации 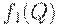 по
по 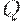 . При этом возможная величина поставки принимает дискретные значения,
. При этом возможная величина поставки принимает дискретные значения, 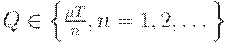
Изучим функцию 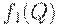 , определенную при
, определенную при 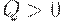 . При приближении к 0 она ведет себя как гипербола, при росте аргумента - как линейная функция. Производная имеет вид
. При приближении к 0 она ведет себя как гипербола, при росте аргумента - как линейная функция. Производная имеет вид
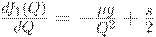
Производная монотонно возрастает, поэтому рассматриваемая функция имеет единственный минимум в точке, в которой производная равна 0, т.е. при
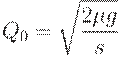
| (34) |
Получена знаменитая " формула квадратного корня".
В литературе иногда без всяких комментариев рекомендуют использовать напряженный план, в котором размеры всех поставляемых партий равны 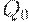 . К сожалению, получаемый таким путем план почти всегда не является оптимальным, т.е. популярная рекомендация неверна или не вполне корректна. Дело в том, что почти всегда
. К сожалению, получаемый таким путем план почти всегда не является оптимальным, т.е. популярная рекомендация неверна или не вполне корректна. Дело в том, что почти всегда
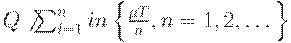
Всегда можно указать неотрицательное целое число 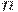 такое, что
такое, что
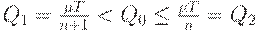
| (35) |
Утверждение 3. Решением задачи оптимизации
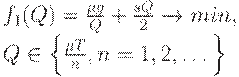
является либо 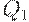 , либо
, либо 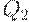 .
.
Действительно, из всех 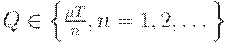 часть лежит правее
часть лежит правее 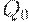 , из них наименьшим является
, из них наименьшим является 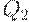 , а часть лежит левее
, а часть лежит левее 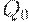 , из них наибольшим является
, из них наибольшим является 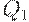 . Для построения оптимального плана обратим внимание на то, что производная функции
. Для построения оптимального плана обратим внимание на то, что производная функции 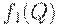 отрицательна левее
отрицательна левее 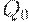 и положительна правее
и положительна правее 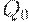 , следовательно, функция средних издержек
, следовательно, функция средних издержек 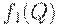 убывает левее
убывает левее 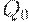 и возрастает правее
и возрастает правее 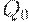 . Значит, минимум по
. Значит, минимум по 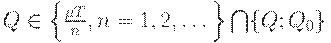 достигается при
достигается при  , а минимум по
, а минимум по 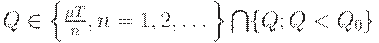 - при
- при  Последнее утверждение эквивалентно заключению утверждения 3.
Последнее утверждение эквивалентно заключению утверждения 3.
Итак, алгоритм построения оптимального плана таков.
1. Найти 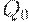 по формуле квадратного корня (34).
по формуле квадратного корня (34).
2. Найти n из условия (35).
3. Рассчитать 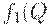 ) по формуле (33) для
) по формуле (33) для  и
и  , где
, где 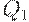 и
и 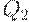 определены в (35).
определены в (35).
4. Наименьшее из двух чисел  и
и 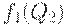 является искомым минимумом, а то из чисел
является искомым минимумом, а то из чисел 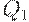 и
и 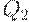 , на котором достигается минимум - решением задачи оптимизации. Обозначим его
, на котором достигается минимум - решением задачи оптимизации. Обозначим его 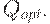
Оптимальный план поставки - это напряженный план, в котором объемы всех поставок равны 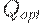 .
.
Замечание. Если 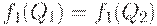 , то решение задачи оптимизации состоит из двух точек
, то решение задачи оптимизации состоит из двух точек 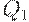 и
и 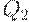 . В этом частном случае существует два оптимальных плана.
. В этом частном случае существует два оптимальных плана.
Пример 1. На складе хранится некоторая продукция, пользующаяся равномерным спросом. За 1 день со склада извлекается 5 т продукции. Плата за хранение 1 т продукции в день - 50 руб. Плата на доставку одной партии - 980 руб. Горизонт планирования - 10 дней. Найти оптимальный план поставок.
В рассматриваемом случае 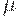 =5 (т/день),
=5 (т/день), 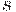 =50 (руб./т.день),
=50 (руб./т.день), 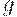 =980 (руб./партия),
=980 (руб./партия),  = 10 (дней). По формуле (34) рассчитываем
= 10 (дней). По формуле (34) рассчитываем
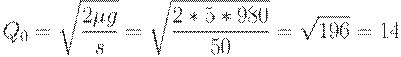
Множество допустимых значений для 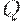 имеет вид
имеет вид
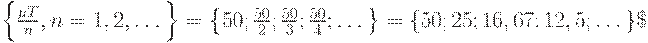
Следовательно, 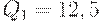 и
и 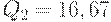 . Первое значение определяет напряженный план с четырьмя одинаковыми зубцами, а второе - с тремя. Поскольку
. Первое значение определяет напряженный план с четырьмя одинаковыми зубцами, а второе - с тремя. Поскольку
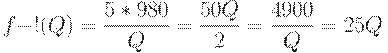
то
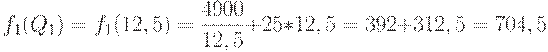
и
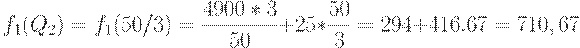
Поскольку 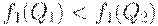 , то
, то  . Итак, оптимальным является напряженный план с четырьмя зубцами.
. Итак, оптимальным является напряженный план с четырьмя зубцами.
Как уже отмечалось, часто рекомендуют применять план поставок с  . Каков при этом проигрыш по сравнению с оптимальным планом?
. Каков при этом проигрыш по сравнению с оптимальным планом?
Для плана с  интервал между поставками составляет
интервал между поставками составляет 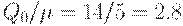 дня. Следовательно, партии придут в моменты
дня. Следовательно, партии придут в моменты 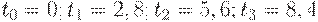 . Следующая партия должна была бы придти уже за пределами горизонта планирования
. Следующая партия должна была бы придти уже за пределами горизонта планирования 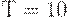 , в момент
, в момент 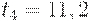 . Таким образом, график уровня запаса на складе в пределах горизонта планирования состоит из трех полных зубцов и одного не полного. К моменту
. Таким образом, график уровня запаса на складе в пределах горизонта планирования состоит из трех полных зубцов и одного не полного. К моменту 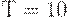 пройдет
пройдет 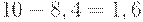 дня с момента последней поставки, значит, со склада будет извлечено
дня с момента последней поставки, значит, со склада будет извлечено 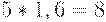 т продукции и останется
т продукции и останется 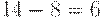 т. План с
т. План с  не является напряженным, а потому не является оптимальным для горизонта планирования
не является напряженным, а потому не является оптимальным для горизонта планирования 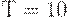 .
.
Подсчитаем общие издержки в плане с  . Площадь под графиком уровня запаса на складе равна сумме площадей трех треугольников и трапеции. Площадь треугольника равна
. Площадь под графиком уровня запаса на складе равна сумме площадей трех треугольников и трапеции. Площадь треугольника равна 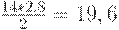 трех треугольников - 58, 8. Основания трапеции параллельны оси ординат и равны значениям уровня запаса в моменты времени
трех треугольников - 58, 8. Основания трапеции параллельны оси ординат и равны значениям уровня запаса в моменты времени 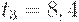 и
и 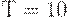 , т.е. величинам 14 и 6 соответственно. Высота трапеции лежит на оси абсцисс и равна
, т.е. величинам 14 и 6 соответственно. Высота трапеции лежит на оси абсцисс и равна 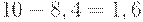 , а потому площадь трапеции есть
, а потому площадь трапеции есть 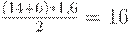 Следовательно, площадь под графиком равна
Следовательно, площадь под графиком равна 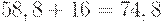 , а плата за хранение составляет
, а плата за хранение составляет 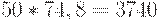 руб.
руб.
За 10 дней доставлены 4 партии товара (в моменты 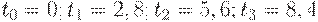 ), следовательно, затраты на доставку равны
), следовательно, затраты на доставку равны 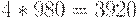 руб. Общие издержки за 10 дней составляют
руб. Общие издержки за 10 дней составляют 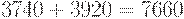 руб., а средние издержки - 766 руб. Они больше средних издержек в оптимальном плане в
руб., а средние издержки - 766 руб. Они больше средних издержек в оптимальном плане в 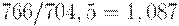 раза, т.е. на 8, 7%.
раза, т.е. на 8, 7%.
Отметим, что
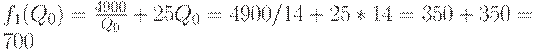
т.е. меньше, чем в оптимальном плане. Таким образом, из-за дискретности множества допустимых значений средние издержки возросли на 4, 5 руб., т.e. на 0, 64%. При этом оптимальный размер партии (12, 5 т) отличается от  т на 1, 5 т, т.е.
т на 1, 5 т, т.е. 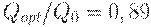 - различие на 11%. Достаточно большое различие объемов поставок привело к пренебрежимо малому изменению функции
- различие на 11%. Достаточно большое различие объемов поставок привело к пренебрежимо малому изменению функции 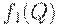 . Это объясняется тем, что в точке
. Это объясняется тем, что в точке 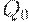 функция
функция 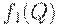 достигает минимума, а потому ее производная в этой точке равна 0.
достигает минимума, а потому ее производная в этой точке равна 0.
Оба слагаемых в 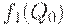 равны между собой. Случайно ли это? Покажем, что нет. Действительно,
равны между собой. Случайно ли это? Покажем, что нет. Действительно,
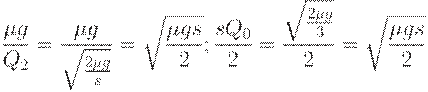
образом, составляющие средних издержек, порожденные различными причинами, уравниваются между собой.
Средние издержки в плане с  равны
равны 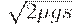 . Интервал между поставками при этом равен
. Интервал между поставками при этом равен
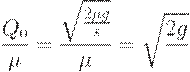
Издержки в течение одного интервала между поставками таковы:
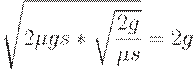
при этом половина (т.е. 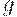 ) приходится на оплату доставки партии, а половина - на хранение товара.
) приходится на оплату доставки партии, а половина - на хранение товара.
Асимптотически оптимальный план. Из проведенных рассуждений ясно, что напряженный план с  является оптимальным тогда и только тогда, когда горизонт планирования Т приходится на начало очередного зубца, т.е. для
является оптимальным тогда и только тогда, когда горизонт планирования Т приходится на начало очередного зубца, т.е. для
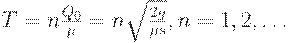
| (36) |
Для всех остальных возможных горизонтов планирования  этот план не является оптимальным. Оптимальным будет напряженный план с другим размером поставки. Для дальнейшего весьма существенно, что при изменении горизонта планирования
этот план не является оптимальным. Оптимальным будет напряженный план с другим размером поставки. Для дальнейшего весьма существенно, что при изменении горизонта планирования  от 0 до
от 0 до 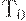 оптимальный план меняется на всем интервале
оптимальный план меняется на всем интервале 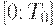 .
.
Как происходит это изменение? При малых горизонтах планирования  делается лишь одна поставка (в момент времени
делается лишь одна поставка (в момент времени 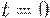 ), график уровня запаса на складе состоит из одного зубца. При увеличении
), график уровня запаса на складе состоит из одного зубца. При увеличении  размер зубца плавно увеличивается. В некоторый момент
размер зубца плавно увеличивается. В некоторый момент 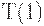 происходит переход от одного зубца к двум. В этот момент оптимальны сразу два плана поставки - с одним зубцом и с двумя. При переходе к планам с двумя зубцами размер зубца скачком уменьшается. При дальнейшем увеличении горизонта планирования оптимальный план описывается графиком с двумя одинаковыми зубцами, размер которых плавно растет. Далее в момент
происходит переход от одного зубца к двум. В этот момент оптимальны сразу два плана поставки - с одним зубцом и с двумя. При переходе к планам с двумя зубцами размер зубца скачком уменьшается. При дальнейшем увеличении горизонта планирования оптимальный план описывается графиком с двумя одинаковыми зубцами, размер которых плавно растет. Далее в момент 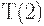 становится оптимальным план с тремя зубцами, размер которых в этот момент скачком уменьшается (в компенсацию за увеличение числа скачков). И т.д.
становится оптимальным план с тремя зубцами, размер которых в этот момент скачком уменьшается (в компенсацию за увеличение числа скачков). И т.д.
Проблема состоит в том, что в реальной экономической ситуации выбор горизонта планирования Т весьма субъективен. Возникает вопрос, какой план разумно использовать, если горизонт планирования не известен заранее. Проблема горизонта планирования возникает не только в логистике. Она является общей для любого перспективного планирования, поэтому весьма важна для стратегического менеджмента. Для решения проблемы горизонта планирования необходимо использование конкретной модели принятия решений, в рассматриваемом случае - классической модели управления запасами.
Ответ можно указать, если горизонт планирования является достаточно большим. Оказывается можно использовать план, в котором все размеры поставок равны 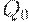 . Для него уровень запаса на складе описывается функцией
. Для него уровень запаса на складе описывается функцией 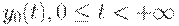 , состоящей из зубцов высоты
, состоящей из зубцов высоты 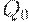 . Предлагается пользоваться планом, являющимся сужением этого плана на интервал
. Предлагается пользоваться планом, являющимся сужением этого плана на интервал  . Другими словами, предлагается на интервале
. Другими словами, предлагается на интервале  использовать начальный отрезок этого плана. Он состоит из некоторого количества треугольных зубцов, а последний участок графика, описываемый трапецией, соответствует тому, что последняя поставка для почти всех горизонтов планирования не будет израсходована до конца. Такой план иногда называют планом Вильсона.
использовать начальный отрезок этого плана. Он состоит из некоторого количества треугольных зубцов, а последний участок графика, описываемый трапецией, соответствует тому, что последняя поставка для почти всех горизонтов планирования не будет израсходована до конца. Такой план иногда называют планом Вильсона.
Ясно, что этот план не будет оптимальным (для всех  , кроме заданных формулой (36)). Действительно, план Вильсона можно улучшить, уменьшив объем последней поставки. Однако у него есть то полезное качество, что при изменении горизонта планирования его начальный отрезок не меняется. Действительно, планы поставок для горизонтов планирования
, кроме заданных формулой (36)). Действительно, план Вильсона можно улучшить, уменьшив объем последней поставки. Однако у него есть то полезное качество, что при изменении горизонта планирования его начальный отрезок не меняется. Действительно, планы поставок для горизонтов планирования 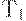 и
и 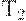 , определенные с помощью функции
, определенные с помощью функции 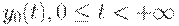 , задающей уровень запасов на складе, совпадают на интервале
, задающей уровень запасов на складе, совпадают на интервале 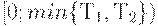 .
.
Определение. Асимптотически оптимальным планом называется план поставок - функция 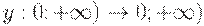 такая, что
такая, что
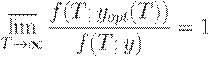
где 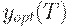 - оптимальный план на интервале
- оптимальный план на интервале  .
.
В соответствии с определениями и обозначениями, введенными в начале раздела, 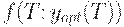 - средние издержки за время
- средние издержки за время  для плана
для плана 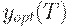 , определенного на интервале
, определенного на интервале  , а
, а 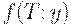 - средние издержки за время
- средние издержки за время  для плана
для плана 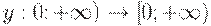 .
.
Теорема 1. План y = y0 является асимптотически оптимальным.
Таким образом, для достаточно больших горизонтов планирования  планы
планы 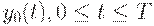 , все зубцы у которых имеют высоту
, все зубцы у которых имеют высоту 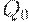 , имеют издержки, приближающиеся к минимальным. Следовательно, эти планы Вильсона, являющиеся сужениями одной и той же функции
, имеют издержки, приближающиеся к минимальным. Следовательно, эти планы Вильсона, являющиеся сужениями одной и той же функции 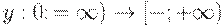 на интервалы
на интервалы  при различных
при различных  , можно использовать одновременно при всех достаточно больших
, можно использовать одновременно при всех достаточно больших  .
.
Замечание. Pешение проблемы горизонта планирования состоит в использовании асимптотически оптимальных планов, которые близки (по издержкам) к оптимальным планам сразу при всех достаточно больших  .
.
Доказательство. По определению оптимального плана
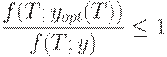
| (37) |
Найдем нижнюю границу для рассматриваемого отношения. При фиксированном  можно указать неотрицательное целое число n такое, что
можно указать неотрицательное целое число n такое, что
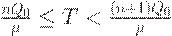
Так как  и
и 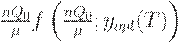 - общие издержки на интервалах
- общие издержки на интервалах 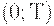 и
и  соответственно при использовании оптимального на
соответственно при использовании оптимального на 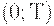 плана, то, очевидно, поскольку второй интервала - часть первого (или совпадает с ним), первые издержки больше вторых, т.е.
плана, то, очевидно, поскольку второй интервала - часть первого (или совпадает с ним), первые издержки больше вторых, т.е.
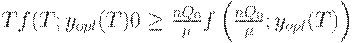
Далее, т.к. на интервале  , включающем целое число периодов плана
, включающем целое число периодов плана 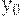 , оптимальным является начальный отрезок этого плана
, оптимальным является начальный отрезок этого плана 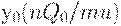 , то
, то
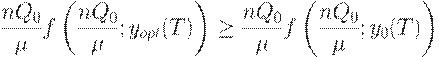
В правой части последнего неравенства стоит 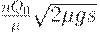 (здесь использована формула для минимального значения средних издержек
(здесь использована формула для минимального значения средних издержек 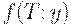 при
при  , кратном
, кратном 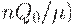 . Из проведенных рассуждений вытекает, что
. Из проведенных рассуждений вытекает, что
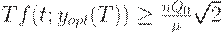
| (38) |
Для общих издержек на интервалах 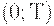 и
и 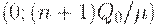 при использовании плана
при использовании плана 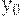 , очевидно, справедливо следующее неравенство
, очевидно, справедливо следующее неравенство
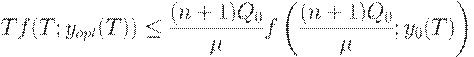
Следовательно,
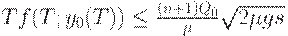
| (39) |
Из неравенств (38) и (39) вытекает, что
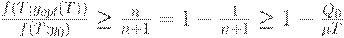
Так как 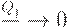 при
при 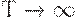 , то, учитывая неравенство (37), из последнего неравенства выводим справедливость заключения теоремы 1. Таким образом, асимптотическая оптимальность плана
, то, учитывая неравенство (37), из последнего неравенства выводим справедливость заключения теоремы 1. Таким образом, асимптотическая оптимальность плана 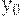 доказана.
доказана.
При небольшом  средние издержки в плане Вильсона могут существенно превышать средние издержки в оптимальном плане. Превышение вызвано скачками функции
средние издержки в плане Вильсона могут существенно превышать средние издержки в оптимальном плане. Превышение вызвано скачками функции 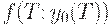 , связанными с переходами через моменты прихода очередных поставок (и увеличением общих издержек скачком на величину платы за доставку партии). Величину превышения средних издержек в плане Вильсона по сравнению с оптимальными планами можно рассчитать.
, связанными с переходами через моменты прихода очередных поставок (и увеличением общих издержек скачком на величину платы за доставку партии). Величину превышения средних издержек в плане Вильсона по сравнению с оптимальными планами можно рассчитать.
Пусть горизонт планирования 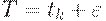 , где
, где 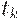 - момент прихода
- момент прихода 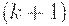 -й поставки в плане Вильсона,
-й поставки в плане Вильсона, 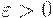 . Тогда, как можно доказать,
. Тогда, как можно доказать,
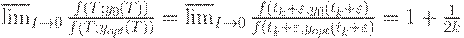
Таким образом, затраты в плане Вильсона являются минимальными (относительно оптимального плана) при  где
где 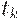 - моменты прихода поставок. Напомним, что план Вильсона является оптимальным при указанных
- моменты прихода поставок. Напомним, что план Вильсона является оптимальным при указанных  . Однако при
. Однако при  , бесконечно близком к
, бесконечно близком к 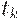 , но превосходящем
, но превосходящем 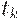 , затраты увеличиваются по сравнению с затратами в оптимальном плане в
, затраты увеличиваются по сравнению с затратами в оптимальном плане в 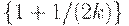 раз. При дальнейшем возрастании Т отношение издержек (средних или общих) в плане Вильсона к аналогичным издержкам в оптимальном плане постепенно уменьшается, приближаясь к 1 при приближении (снизу) к моменту
раз. При дальнейшем возрастании Т отношение издержек (средних или общих) в плане Вильсона к аналогичным издержкам в оптимальном плане постепенно уменьшается, приближаясь к 1 при приближении (снизу) к моменту 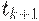 прихода следующей поставки. А там - новый скачок, но уже на меньшую величину
прихода следующей поставки. А там - новый скачок, но уже на меньшую величину 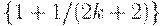 . И т.д.
. И т.д.
Сразу после прихода первой поставки отношение затрат составляет 1, 5 (превышение на 50%), после прихода второй - 1, 25 (превышение на 25%), третьей - 1, 167 (превышение на 16, 7%), четвертой - 1, 125 (превышение на 12, 5%), пятой - 1, 1 (превышение на 10%), и т.д. Таким образом, при небольших горизонтах планирования Т превышение затрат может быть значительным, план Вильсона отнюдь не оптимальный. Но чем больше горизонт планирования, тем отклонение меньше. Уже после сотой поставки оно не превышает 0, 5%.
Влияние отклонений от оптимального объема партии. В реальных производственных и управленческих ситуациях часто приходится принимать решения об использовании объемов партии, отличных от оптимальной величины 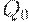 , рассчитанной по формуле квадратного корня (34). Например, при ограниченной емкости склада или для обеспечения полной загрузки транспортных средств большой вместимости. Это возможно также в ситуации, когда величина партии измеряется в целых числах (штучный товар) или даже в десятках, дюжинах, упаковках, ящиках, контейнерах и т.д., а величина
, рассчитанной по формуле квадратного корня (34). Например, при ограниченной емкости склада или для обеспечения полной загрузки транспортных средств большой вместимости. Это возможно также в ситуации, когда величина партии измеряется в целых числах (штучный товар) или даже в десятках, дюжинах, упаковках, ящиках, контейнерах и т.д., а величина 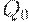 не удовлетворяет этому требованию и, следовательно, не может быть непосредственно использована в качестве объема поставки.
не удовлетворяет этому требованию и, следовательно, не может быть непосредственно использована в качестве объема поставки.
Поэтому необходимо уметь вычислять возрастание средних издержек при использовании напряженного плана с одинаковыми поставками объема 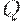 , отличного от
, отличного от 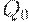 , по сравнению со средними издержками в оптимальном плане. Будем сравнивать средние издержки за целое число периодов. Как показано выше, они имеют вид
, по сравнению со средними издержками в оптимальном плане. Будем сравнивать средние издержки за целое число периодов. Как показано выше, они имеют вид
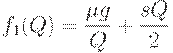
где 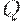 - объем партии. Тогда
- объем партии. Тогда
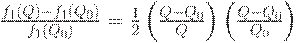
| (40) |
Это тождество нетрудно проверить с помощью простых алгебраических преобразований.
Пример 2. Пусть используется план с 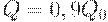 . Тогда
. Тогда
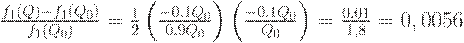
Таким образом, изменение объема партии на 10% привело к увеличению средних издержек лишь на 0, 56%.
Пример 3. Пусть используемое значение объема поставки 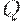 отличается от оптимального не более чем на 30%. На сколько могут возрасти издержки?
отличается от оптимального не более чем на 30%. На сколько могут возрасти издержки?
Из формулы (40) вытекает, что максимальное возрастание издержек будет в случае 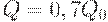 . Тогда
. Тогда
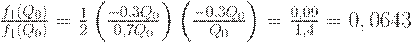
Таким образом, издержки могут возрасти самое большее на 6, 43%.
На первый взгляд представляется удивительным, что сравнительно большое отклонение значения переменной 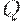 от оптимального (на 30%) приводит к столь малому возрастанию значения оптимизируемой функции. Этот факт имеет большое прикладное значение. Из него следует, что область " почти оптимальных" значений параметра весьма обширна, следовательно, из нее можно выбирать для практического использования те или иные значения, исходя из иных принципов. Можно, например, минимизировать какую-либо иную целевую функцию, тем самым, решая задачу многокритериальной оптимизации. Можно " вписаться" в действующую дискретную систему возможных значений параметров. И т.д.
от оптимального (на 30%) приводит к столь малому возрастанию значения оптимизируемой функции. Этот факт имеет большое прикладное значение. Из него следует, что область " почти оптимальных" значений параметра весьма обширна, следовательно, из нее можно выбирать для практического использования те или иные значения, исходя из иных принципов. Можно, например, минимизировать какую-либо иную целевую функцию, тем самым, решая задачу многокритериальной оптимизации. Можно " вписаться" в действующую дискретную систему возможных значений параметров. И т.д.
Важное замечание 1. Обширность области " почти оптимальных" значений параметра - общее свойство оптимальных решений, получаемых путем минимизации гладких функций. Действительно, пусть необходимо минимизировать некоторую функцию 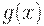 , трижды дифференцируемую. Пусть минимум достигается в точке
, трижды дифференцируемую. Пусть минимум достигается в точке 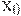 . Справедливо разложение Тейлора-Маклорена
. Справедливо разложение Тейлора-Маклорена
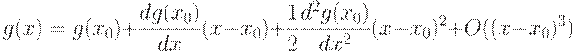
Однако в х0 выполнено необходимое условие экстремума (в данном случае - минимума)
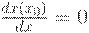
Следовательно, с точностью до бесконечно малых более высокого порядка (по сравнению с 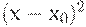 ) справедливо равенство
) справедливо равенство
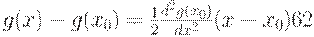
| (41) |
Это соотношение показывает, что приращение значений минимизируемой функции - бесконечно малая более высокого порядка по сравнению с приращением независимой переменной. Если
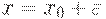
то
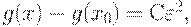
где
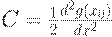
Вернемся к классической модели управления запасами. Для нее надо рассматривать 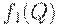 в роли
в роли 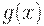 . С помощью соотношения (41) заключаем, что
. С помощью соотношения (41) заключаем, что
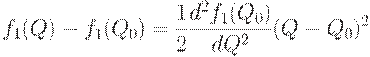
с точностью до бесконечно малых более высокого порядка. Вычислим вторую производную 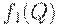 . Поскольку
. Поскольку
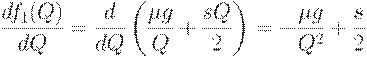
то
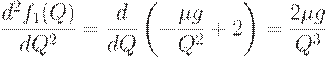
Теперь заметим, что
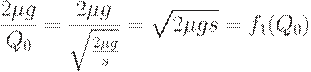
Следовательно,
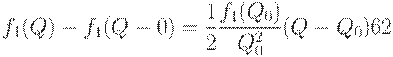
с точностью до бесконечно малых более высокого порядка. Отличие этой формулы от точной формулы (40) состоит только в том, что 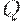 в знаменателе одной из дробей заменено на
в знаменателе одной из дробей заменено на 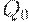 .
.
Устойчивость выводов в математической модели. Вполне ясно, что рассматриваемая классическая модель управления запасами, как и любые иные экономико-математические модели конкретных экономических явлений и процессов, является лишь приближением к реальности. Приближение может быть более точным или менее точным, но никогда не может полностью уловить все черты реальности. Поэтому с целью повышения адекватности получаемых на основе экономико-математической модели выводов целесообразно изучить устойчивость этих выводов по отношению к допустимым отклонениям исходных данных и предпосылок модели. Выше изучено изменение средних издержек при малых отклонениях величины поставки.
Предположим теперь, что вместо истинных значений параметров µ, g, s нам известны лишь их приближенные значения 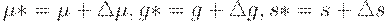 . Мы применяем план Вильсона, но с искаженным объемом партии
. Мы применяем план Вильсона, но с искаженным объемом партии
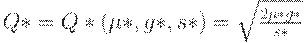
Это приводит к возрастанию средних издержек. Согласно формулам (40) - (41) возрастание пропорционально 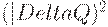 (с точностью до бесконечно малых более высокого порядка). Здесь
(с точностью до бесконечно малых более высокого порядка). Здесь
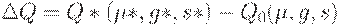
Выделим в 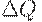 главный линейный член:
главный линейный член:
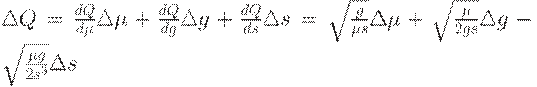
| (42) |
(с точностью до бесконечно малых более высокого порядка).
Величину 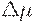 можно определить по фактическим данным о спросе, оценив величину отклонения реального спроса от линейного приближения, например, с помощью математического аппарата линейного регрессионного анализа. Для определения значений параметров
можно определить по фактическим данным о спросе, оценив величину отклонения реального спроса от линейного приближения, например, с помощью математического аппарата линейного регрессионного анализа. Для определения значений параметров 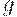 и
и 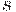 необходимо проведение специальных трудоемких исследований. К тому же существуют различные методики расчета этих параметров, результаты расчетов по которым не совпадают. Поэтому естественно оценить разумную точность определения g и s по известной точности определения
необходимо проведение специальных трудоемких исследований. К тому же существуют различные методики расчета этих параметров, результаты расчетов по которым не совпадают. Поэтому естественно оценить разумную точность определения g и s по известной точности определения 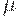 . Для этого воспользуемся " принципом уравнивания погрешностей", предложенным в.
. Для этого воспользуемся " принципом уравнивания погрешностей", предложенным в.
Важное замечание 2. Принцип уравнивания погрешностей состоит в том, что погрешности различной природы должны вносить примерно одинаковый вклад в общую погрешность математической модели. Так, определение рационального объема выборки в статистике интервальных данных основано на уравнивании влияния метрологической и статистической погрешностей. Согласно подходу [13.15] выбор числа градаций в социологических анкетах целесообразно проводить на основе уравнивания погрешностей квантования и неопределенности в ответах респондентов. В классической модели управления запасами целесообразно уравнять влияние неточностей в определении параметров на отклонение целевой функции от оптимума.
Выберем 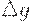 и
и 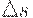 так, чтобы увеличение затрат, вызванное неточностью определения
так, чтобы увеличение затрат, вызванное неточностью определения 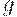 и
и 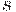 , было таким же, как и вызванное неточностью определения
, было таким же, как и вызванное неточностью определения 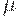 . С точностью до бесконечно малых более высокого порядка это означает, что необходимо уравнять между собой три слагаемых в правой части (42). После сокращения общего множителя получаем, что согласно принципу уравнивания погрешностей должно быть справедливо соотношение
. С точностью до бесконечно малых более высокого порядка это означает, что необходимо уравнять между собой три слагаемых в правой части (42). После сокращения общего множителя получаем, что согласно принципу уравнивания погрешностей должно быть справедливо соотношение
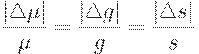
| (43) |
Таким образом, относительные погрешности определения параметров модели должны совпадать.
В соотношении (43) используются истинные значения параметров, которые неизвестны. Поэтому целесообразно вначале вместо параметров использовать их грубые оценки, из (43) определить их примерную точность, затем провести исследования, уточняющие значения параметров. Эту процедуру естественно повторять до тех пор, пока не произойдет некоторое уравнивание относительных погрешностей определения параметров модели.
Модель с дефицитом. Классическая модель управления запасами может быть обобщена в различных направлениях. Одно из наиболее естественных обобщений - введение в модель возможности дефицита.
В рассматриваемой до сих пор модели предполагалось, что дефицит не допускается, т.е. некоторое количество товара на складе всегда есть. Но, может быть, выгоднее сэкономить на расходах по хранению запаса, допустив небольшой дефицит - потребность в товаре в некоторые интервалы времени может остаться неудовлетворенной?
Как подсчитать убытки от дефицита, в частности, от потери доверия потребителя? Будем считать, что если нет товара, владеющая складом организация платит штраф - каждый день пропорционально нехватке. По приходе очередной поставки все накопленные требования сразу же удовлетворяются.
Сохраним все предположения и обозначения рассматриваемой до сих пор модели, кроме отсутствия дефицита. Неудовлетворенный спрос будем рассматривать как отрицательный запас. График изменения величины запаса на складе изображен на рис.13.3.
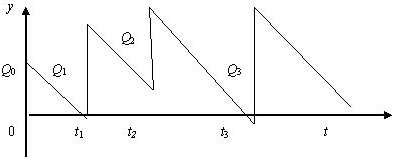
Рис. 13.3. График изменения величины запаса на складе при возможности дефицита
Очевидно, рис.13.1 и рис.13.3 отличаются только тем, что на последнем рисунке зубцы графика могут опускаться ниже оси абсцисс, что соответствует сдвигу графика рис.13.1 как единого целого вниз вдоль оси ординат.
Пусть 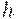 - плата за нехватку единицы товара в единицу времени (например, в день). Тогда средние издержки за время
- плата за нехватку единицы товара в единицу времени (например, в день). Тогда средние издержки за время  определяются формулой
определяются формулой
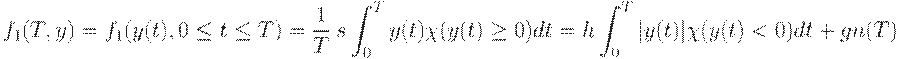
где 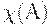 - индикатор множества
- индикатор множества 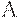 , т.е.
, т.е. 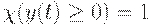 при
при 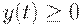 и
и 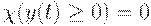 при
при 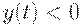 , в то время как
, в то время как 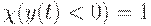 при
при 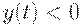 и
и 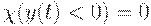 при
при 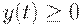 . Таким образом, площадь под частью графика уровня запаса, лежащей выше оси абсцисс, берется с множителем
. Таким образом, площадь под частью графика уровня запаса, лежащей выше оси абсцисс, берется с множителем 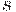 , а площадь между осью абсцисс и частью графика
, а площадь между осью абсцисс и частью графика 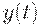 , соответствующей отрицательным значениям запаса, берется с заметно большим по величине множителем
, соответствующей отрицательным значениям запаса, берется с заметно большим по величине множителем 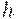 .
.
Для модели с дефицитом оптимальный план находится почти по той же схеме, что и для модели без дефицита. Сначала фиксируем моменты поставок и находим при этом условии оптимальные размеры поставок. Фактически речь идет о выборе уровня запаса 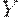 в момент прихода очередной поставки (рис.13.4).
в момент прихода очередной поставки (рис.13.4).
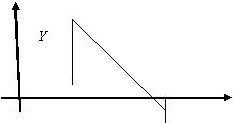
Рис. 13.4. Первый шаг построения оптимального плана в модели с дефицитом
Увеличивая или уменьшая 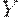 , можно увеличивать или уменьшать площадь треугольника над осью абсцисс (учитываемую с коэффициентом
, можно увеличивать или уменьшать площадь треугольника над осью абсцисс (учитываемую с коэффициентом 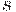 ) и соответственно уменьшать или увеличивать площадь треугольника под осью абсцисс (учитываемую с коэффициентом
) и соответственно уменьшать или увеличивать площадь треугольника под осью абсцисс (учитываемую с коэффициентом 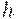 ), добиваясь минимизации взвешенной суммы этих площадей. Все элементы прямоугольных треугольников на рис.13.4 выражаются через
), добиваясь минимизации взвешенной суммы этих площадей. Все элементы прямоугольных треугольников на рис.13.4 выражаются через 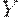 , заданный интервал времени между поставками и параметры модели. Минимизация соответствующего квадратного трехчлена дает оптимальное значение
, заданный интервал времени между поставками и параметры модели. Минимизация соответствующего квадратного трехчлена дает оптимальное значение
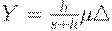
При этом минимальная сумма затрат на хранение и издержек, вызванных дефицитом, равна
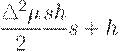
Второй шаг нахождения оптимального плана в модели с дефицитом полностью совпадает с аналогичным рассуждением в исходной модели. Фиксируется число поставок, и с помощью варьирования размеров интервалов между поставками минимизируется целевой функционал. Поскольку сумма квадратов некоторого числа переменных при заданной их сумме достигает минимума, когда все эти переменные равны между собой, то оптимальным планом является план, у которого все зубцы одинаковы, т.е. уровень запаса в момент прихода очередной поставки - всегда один и тот же. При этом все объемы поставок, за исключением объема начальной поставки (в нулевой момент времени), равны между собой:

| (44) |
На третьем этапе среди указанного однопараметрического дискретного множества планов находим оптимальный план. Как и для модели без дефицита, в качестве ориентира используется план с размером поставки, определяемой по формуле квадратного корня,
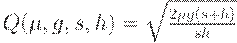
Для горизонтов планирования  , кратных
, кратных 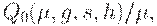 оптимальным является
оптимальным является