Задачи для самостоятельного решения. 1. Орграф задан матрицей смежности

1. Орграф задан матрицей смежности. Определить матрицу сильной связности S(D). Используя алгоритм найти количество компонент сильной связности орграфа D и определить матрицы смежности этих компонент. Построить изображение орграфа и его компонент сильной связности.

а) 0 1 0 0 1 0 б) 0 1 0 0 0

0 0 0 0 0 1 1 0 0 0 0

0 1 0 1 0 0 A(D)= 0 1 0 1 0

A(D)= 0 0 1 0 0 1 0 0 0 0 1

1 0 0 1 0 1 0 0 1 0 0

0 1 0 0 0 0

2.Форма отчета

1.Разобрать решенные задачи и записать в тетрадь

2. Выполнить задачи для самостоятельного решения и оценить свою работу по следующей схеме:

1 задача – 3 балла

2 задачи - 5 баллов

Задание на внеаудиторную самостоятельную работу

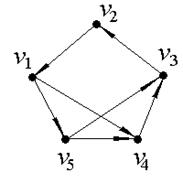
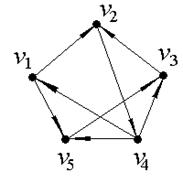
1. С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.

а) б) в)

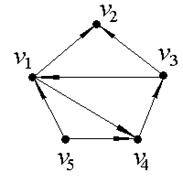
2. Ответить на контрольные вопросы

Контрольные вопросы.

1. Подграф

2. Собственный подграф

3. Компонента связности, сильной связности

4. Матрица достижимости орграфа

5. Матрица сильной связности орграфа

6. Матрица связности графа

7. Нахождение матрицы связности, сильной связности

Литература

1. В.Н. Нефедов «Курс дискретной математики»

г. Москва, изд. МАИ, 2010 год

2. В. Новиков «Курс дискретной математики для программистов»

г. Москва, 2012 год

3.М.С. Спирина, П.А. Спирин «Дискретная математика»- М.: Издательский центр «Академия», 2008 год