
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные понятия. Отчет по лабораторной работе на тему
|
|
Отчет по лабораторной работе на тему
ИССЛЕДОВАНИЕ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ПОСТОЯННОГО ТОКА» по дисциплине
«Электроснабжение с основами электротехники»
Студента направления
Строительство (СТЗС).
Форма обучения - дневная
2 курс
4 семестр
Выполнила:
Студент
Группы б2СТЗС-21
Малахов Роман Александрович
Зечет. Кн. №130458
Проверил:
кандидат технических наук
Сивяков Д.Б.
Саратов 2015
Цель работы: экспериментальное исследование линейной электрической цепи постоянного тока и изучение методов расчета такой цепи.
ОСНОВНЫЕ ПОНЯТИЯ
Электрической цепью называют совокупность устройств, предназначенных для передачи, распределения и взаимного преобразования электрической и других видов энергии, если процессы, протекающие в устройствах, могут быть описаны при помощи понятий об электродвижущей силе (ЭДС), токе и напряжении.
Электрические цепи, в которых получение электрической энергии в источниках, ее передача и преобразование в приемниках происходит при неизменных во времени токах и напряжениях, называют цепями постоянного тока.
Электрические цепи постоянного тока, состоящие только из элементов с линейными вольт-амперными характеристиками, называются линейными.
Ветвью называется участок электрической цепи, который состоит только из последовательно включенных элементов и вдоль которого протекает один и тот же ток.
Узлом электрической цепи называется точка соединения трех и более ветвей.
Контур электрической цепи – это замкнутый путь, проходящий по нескольким ветвям; при этом каждый узел в рассматриваемом контуре встречается не более одного раза. Контур называют независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.
Наиболее часто расчет электрической цепи состоит в определении токов, протекающих по ветвям, под действием заданных источников ЭДС при заданных значениях сопротивлений.
Для расчета линейных электрических цепей постоянного тока существует ряд методов, целесообразность применения которых определяется исходными данными.
Наиболее универсальным является метод применения законов Кирхгофа, которые формулируются следующим образом.
Первый закон Кирхгофа. Алгебраическая сумма токов в любом узле электрической цепи равна нулю:
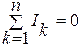 ,
,
то есть в любом узле электрической цепи сумма токов, направленных к узлу, равна сумме токов, направленных от узла.
Второй закон Кирхгофа. В любом контуре электрической цепи алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС контура:
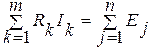 , (1)
, (1)
где m – число резистивных элементов в контуре; n – число ЭДС.
В уравнении (1) со знаком плюс записываются токи и ЭДС, направления которых совпадают с произвольно выбранным направлением обхода контура.
Количество уравнений, составляемых по двум законам Кирхгофа, определяется числом ветвей Вс неизвестными токами. Из них по первому закону Кирхгофа составляется (У–1) уравнений, где У – число узлов. Остальные (В–У+1) уравнений составляются по второму закону Кирхгофа.
Продемонстрируем порядок расчета на примере электрической цепи, представленной на рис. 1.
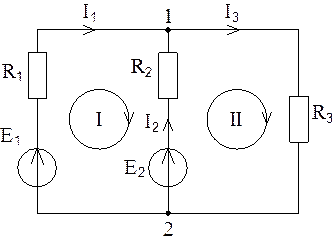
Рис. 1
Дано: E1, Е2, R1, R2, R3.
Необходимо определить токи в ветвях схемы. Для этого выполним следующие действия.
1. Произвольно выберем и укажем на схеме положительные направления токов в ветвях и положительные направления обхода независимых контуров. Примем за положительное направление обхода этих контуров обход по часовой стрелке.
2. Для (У–1) узлов составим уравнение по первому закону Кирхгофа, например, для узла «1»
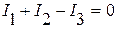 . (2)
. (2)
По второму закону Кирхгофа составим уравнения для независимых контуров:
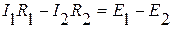 ; (3)
; (3)
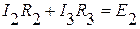 . (4)
. (4)
3. Решая систему уравнений (2) – (4) любым известным методом решения систем линейных алгебраических уравнений, можно определить искомые токи в ветвях.
Чтобы уменьшить число совместно решаемых уравнений по сравнению с числом уравнений, составляемых по закону Кирхгофа, расчет линейных электрических цепей проводят с использованием метода контурных токов или метода узловых потенциалов. Эти методы подробно изложены в литературе, список которой приведен ниже.
Существует метод расчета, который позволяет свести расчет разветвленной цепи с несколькими источниками ЭДС к расчету нескольких цепей, в каждой из которых действует только один источник ЭДС. Этот метод основан на принципе наложения, который формулируется следующим образом: если в электрической цепи действует несколько источников энергии, то ток любой ветви равен алгебраической сумме токов, вызванных действием каждого источника энергии схемы в отдельности.
Порядок расчета цепей методом наложения рассмотрим на примере схемы рис. 1.
1. Исключим источник ЭДС Е2. Соответствующая расчетная схема показана на рис. 2. Обозначим токи, протекающие под действием ЭДС Е1, через I’1, I’2, I’3 и укажем на схеме их направление.
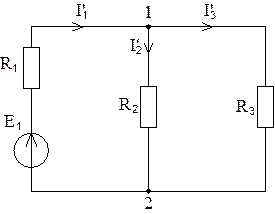
Рис. 2
Из рассмотрения полученной схемы видно, что для ее расчета достаточно использования закона Ома. При этом удобно предварительно определить эквивалентное сопротивление параллельно включенных сопротивлений R2 и R3:
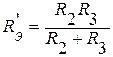 .
.
Ток в первой ветви, обусловленный действием ЭДС Е1:
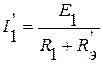 .
.
Токи I’2, I’3 найдем после расчета напряжения между узлами 1 и 2.
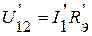 ;
;
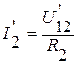 ;
;
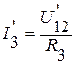 .
.
2. Исключим теперь вместо источника ЭДС Е2 источник ЭДС Е1. Соответствующая расчетная схема показана на рис. 3.
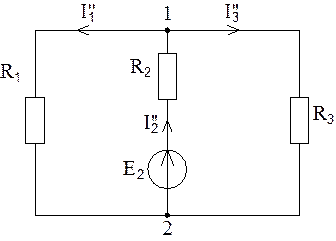
Рис. 3
Обозначим токи, протекающие под действием ЭДС Е2, через I’’1, I’’2, I’’3 и найдем их:
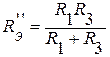 ;
;
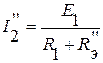 ;
;
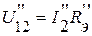 ;
;
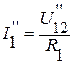 ;
;
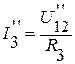 .
.
3. Определим искомые токи в ветвях исходной схемы (рис. 1) наложением токов схем на рис. 2 и на рис. 3, при этом соблюдается следующее правило знаков: если ток, обусловленный отдельным источником ЭДС совпадает по направлению с током исходной схемы, то он берется со знаком “+”, если не совпадает – то со знаком “–“. В нашем случае все токи в промежуточных схемах выбраны совпадающими с направлениями токов в исходной схеме:
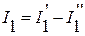 ;
;
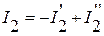 ;
;
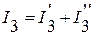 .
.
Еще одним методом, облегчающим расчет простых цепей сводящихся к схеме с двумя узлами является частный случай метода узловых потенциалов – метод двух узлов.
Порядок расчета методом двух узлов также рассмотрим на примере схемы (рис. 1).
1. Рассчитываются проводимости отдельных ветвей:
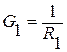 ;
;
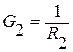 ;
;
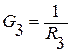 .
.
2. Определяется напряжение между узлами 1 и 2 по формуле
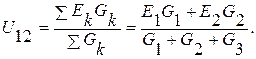
В числителе формулы произведение берут со знаком «+» в том случае, когда ЭДС Еk напралена к узлу 1, и со знаком «–», когда от узла. В рассматриваемом примере обе ЭДС направлены к узлу 1.
3. Теперь токи в ветвях могут быть определены с помощью обобщенного закона Ома:
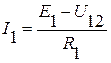 ;
;
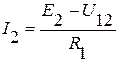 ;
;
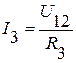 .
.
Таким образом, расчет схем с использованием метода наложения или метода двух узлов не требует решения систем уравнений, а сами вычисления сводятся к решению простых уравнений, составленных с помощью закона Ома.