
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчётно-графическая работа №1.
|
|
Часть 1. Определение реакций опор и усилий в стержнях плоской фермы.
Расчётная схема плоской фермы, образованная шарнирным соединением стержней в форме треугольников, изображена на рисунках 1.0-1.9. Цифрами на схемах пронумерованы узлы фермы (точки, в которых сходятся оси стержней). Ферма закреплена на двух шарнирах (один – подвижный, другой - неподвижный) или на неподвижном шарнире и невесомом стержне.
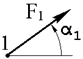
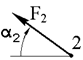
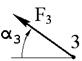
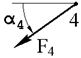
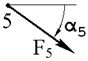
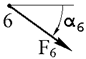
На ферму действуют три внешние силы, приложенные в узлах фермы. Номера узлов, где приложены силы и направление действия сил указаны в таблице 1.1. Геометрические размеры фермы и величины внешних сил указаны в таблице 1.2.
Нумерация рисунков и таблиц в РГР №1 выполнена двумя цифрами, разделёнными точкой. Первая цифра указывает на принадлежность рисунка (таблицы) к первой или ко второй части. Номером рисунка (таблицы) является вторая цифра, стоящая после точки. Например, рисунок 1.3 – это рисунок №3 в первой части работы.
Выбор варианта задания студент осуществляет по своему шифру, образованному тремя последними цифрами номера зачётной книжки. Например, если номер зачётной книжки 261573, то шифр студента будет «573». По третьей (последней) цифре шифра выбирается номер рисунка, по второй (средней) цифре шифра выбирается номер условия (строки) в таблице 1.1; по первой цифре шифра – номер условия (строки) в таблице 1.2.
В каждом варианте заданий требуется определить:
- реакции опор фермы,
- усилия в стержнях фермы.
| Таблица 1.1 | ||||||
| Номер условия | Номер узла и направление действия силы | |||||
| 
| 
| 
|
|
| |
| α 1, град. | α 2, град. | α 3, град. | α 4, град. | α 5, град. | α 6, град. | |
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - |
| Таблица 1.2 | ||||||||
| Номер условия | Размеры, м | Силы, кН | ||||||
| a | h | F1 | F2 | F3 | F4 | F5 | F6 | |
| Таблица 1.3 | |||||||
| N стержня | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 |
| Усилие S, кН | –15, 8 | –25, 8 | –25, 8 | 24, 2 | 24, 3 | ||
| N стержня | 1-8 | 2-8 | 3-8 | 4-8 | 6-4 | 7-4 | |
| Усилие S, кН | –7, 3 | 22, 3 | –22, 3 | –34, 2 |
|
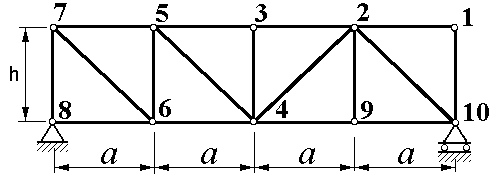
| Рисунок 1.0 |
|
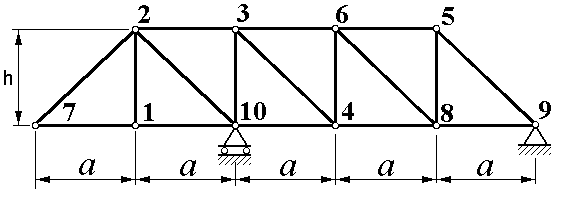
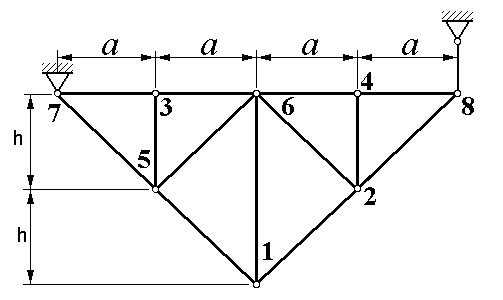
| Рисунок 1.1 |
|
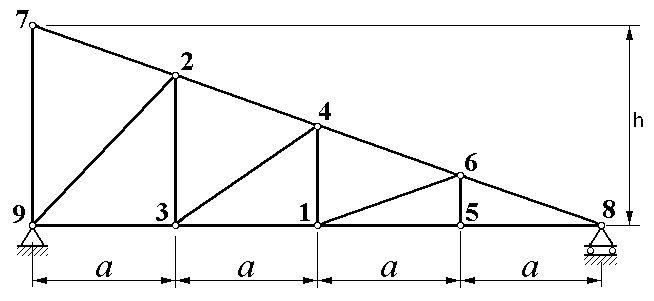
| Рисунок 1.2 |
|
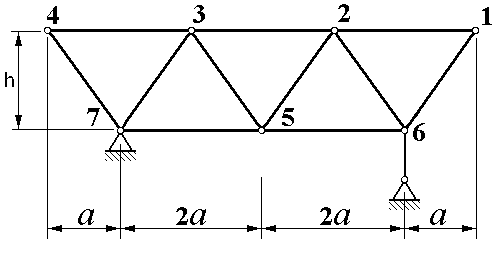
| Рисунок 1.3 |
|
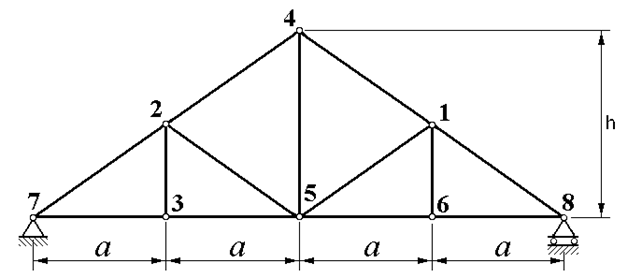
| Рисунок 1.4 |
|
| Рисунок 1.5 |
|
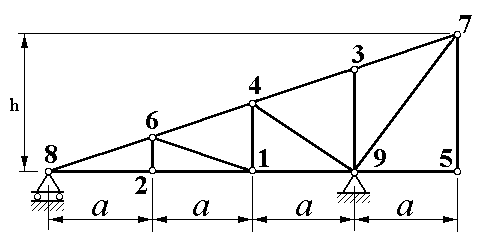
| Рисунок 1.6 |
|
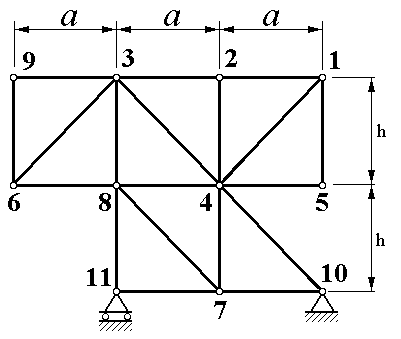
| Рисунок 1.7 |
|
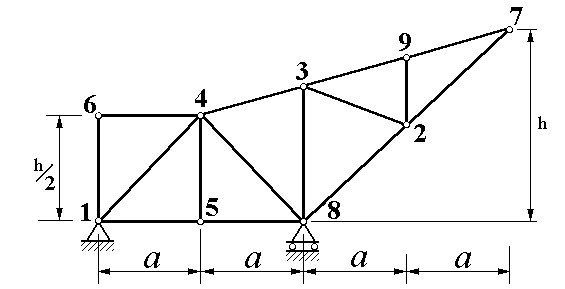
| Рисунок 1.8 |
|
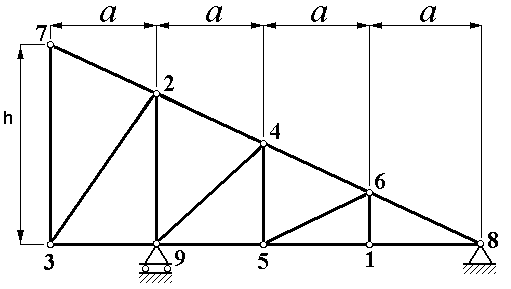
| Рисунок 1.9 |
Указания. Задача первой части на равновесие тела, находящегося под действием произвольной плоской системы сил.
Определение реакции опор рекомендуется выполнить в следующей последовательности. Нарисовать схему фермы, расставить заданные внешние силы, выбрать направление координатных осей, вычислить проекции заданных сил на координатные оси и нанести проекции сил на схему с указанием направления их действия. Значения заданных сил и рассчитанные значения проекций сил целесообразно выписать в табличной форме вблизи схемы фермы, что позволит проверить правильность разложения сил и облегчит использование полученных значений при составлении и решении уравнений равновесия.
Далее необходимо отбросить связи фермы (опорные шарниры и стержень), заменив их соответствующими реакциями. При отбрасывании неподвижного шарнира в состав действующих сил вводятся две составляющих реакции опоры – по оси Х и по оси У.
При отбрасывании подвижного шарнира или стержня вводится по одной реакции: вместо шарнира – перпендикулярно опорной поверхности, вместо стержня – по направлению стержня.
В каждом варианте задания должно быть по три неизвестных реакции, которые подлежат определению из трёх уравнений равновесия. Составлять и решать уравнения равновесия можно в любой последовательности. Однако наиболее рационально начать с уравнения суммы моментов всех сил относительно точки неподвижного шарнира, где две неизвестных реакции, которые не войдут в это уравнение. Затем можно решать уравнения сумм проекций всех сил на координатные оси.
После определения всех трёх реакций необходимо выполнить проверку. Для этого нужно составить и решить уравнение моментов относительно любого узла фермы, через который не проходят линии действия реакций опор.
Определение усилий в стержнях нужно выполнять с использованием двух способов – «вырезанием» узлов и методом сечений.
Однако, прежде чем приступить к расчётам, следует выявить наличие стержней, усилия в которых равны нулю («нулевые стержни»), пользуясь следующими леммами:
Лемма 1. Если в незагруженном узле плоской фермы сходятся два стержня, то усилия в этих стержнях равны нулю.
Лемма 2. Если в незагруженном узле плоской фермы сходятся три стержня, из которых два расположены на одной прямой, то усилие в третьем стержне равно нулю. Усилия в первых двух стержнях равны между собой.
Лемма 3. Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилие в этом стержне по модулю равно приложенной силе, а усилие в другом стержне равно нулю.
Усилие в стержне обозначается буквой S, а номер стержня определяется номерами узлов, между которыми расположен стержень. Так, стержень «4-5» соединяет узел 4 с узлом 5.
Определение усилия в стержнях фермы по методу вырезания узлов сводится к последовательному рассмотрению равновесия отдельных узлов фермы под действием сил, сходящихся в этом узле. Действие отброшенной части фермы заменяется действием реакций перерезанных стержней, численно равных искомым усилиям в стержнях. Эти усилия направляются вдоль стержней от узла, предполагая стержни растянутыми. Если в результате расчёта усилие в стержне окажется со знаком «минус», это означает, что стержень не растянут, а сжат.
Вырезание следует начинать с узла, в котором сходятся два стержня, так как при рассмотрении его равновесия можно составить только два уравнения:
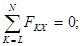
| 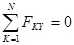
|
как для плоской системы сходящихся сил. При вырезании последующих узлов необходимо следить, чтобы в каждом из них было не более двух стержней с неизвестными усилиями.
К вырезанному узлу прикладывается заданная внешняя сила или определённая ранее опорная реакция. Определение неизвестных усилий можно выполнять аналитическим или графическим методами.
При аналитическом методе для узла выбирается система координат (ХУ) и составляются два уравнения равновесия – суммы проекций всех сил на координатные оси, из которых определяются неизвестные усилия.
При графическом методе решения для сходящейся системы сил вырезанного узла строится многоугольник, который должен быть замкнутым из условия равновесия. Для построения многоугольника сил выбирается масштаб (в 1 см – 5 кН или 10 кН) и произвольная точка. Из этой точки в выбранном масштабе откладываются последовательно вектора известных сил, параллельно линиям их действия, так чтобы последующий вектор пристраивался в конец предыдущего. Затем через начальную точку построения и через конец последнего вектора проводятся по две линии параллельно неизвестным усилиям. Точка пересечения линий действия неизвестных усилий позволяет построить замкнутый многоугольник, из которого находится длина отрезков, соответствующих неизвестным усилиям и направление действия усилий. Длина отрезков с помощью масштаба пересчитывается в величину силы. Направление усилий должно быть таким, чтобы стрелки всех векторов в многоугольнике были ориентированы по контуру в одну сторону.
Графическим методом следует определить усилия как минимум в двух узлах фермы.
При аналитическом решении уравнений равновесия и при графическом решении (построением многоугольника) необходимо руководствоваться следующими правилами знаков:
1. При составлении расчётной схемы каждого последующего узла найденные ранее усилия в стержнях независимо от их знака направляются от узла.
2. При вычислениях определённые ранее усилия берутся с учётом знака.
3. При подстановке усилия из одного уравнения в другое знак «минус» учитывается.
4. При построении силовых многоугольников найденные ранее усилия в стержнях откладываются с учётом знака: если положительное, то направляется от узла, если отрицательное – к узлу.
Для определения усилий во всех стержнях фермы достаточно решить уравнения равновесия для (N-1) узлов.
Проверка правильности определения усилий производится при вырезании последнего узла. Если усилия определены правильно, то уравнения равновесия сил последнего узла должны обратиться в тождество типа 0=0.
Определение усилий в стержнях методом сечений (способ Риттера). Для этого:
а) «разрезаем» мысленно ферму на две части так, чтобы отсекалось не менее двух узлов и оказались «перерезанными» три стержня, усилия в которых (или в одном из которых) нужно определить.
б) рассматриваем равновесие одной из частей фермы, причём действие отброшенной части заменяем действием реакций перерезанных стержней, численно равных искомым усилиям. Эти усилия направляем вдоль перерезанных стержней от узлов, то есть предполагаем стержни растянутыми.
в) составляем уравнения равновесия для выделенной части фермы таким образом, чтобы в каждое уравнение вошло только одно усилие в стержне, которое в данном случае мы хотим определить. Обычно это уравнения моментов всех сил относительно точек, где пересекаются действия двух других неизвестных усилий, или уравнения проекций на ось, перпендикулярную двум другим неизвестным усилиям.
Метод сечений необходимо использовать хотя бы один раз для определения неизвестных усилий в стержнях или для проверки усилий, определённых методом вырезания узлов, – по усмотрению студента.
Пример. Плоская ферма (рисунок 1.10) прикреплена в узле 1 к неподвижному шарниру, а в узле 6 – к подвижному. Действующие на ферму три внешние силы и размеры фермы указаны на рисунке.
Дано: F1=10 кН; F2=20 кН, 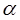 =30º; F3=30 кН; a=2 м; b=2 м.
=30º; F3=30 кН; a=2 м; b=2 м.
Определить опорные реакции и усилия во всех стержнях фермы.
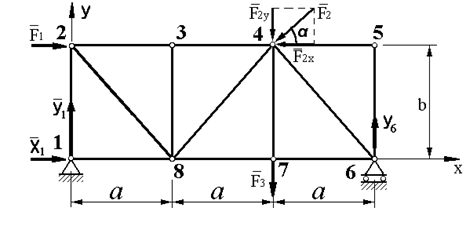
|
| Рисунок 1.10 |