
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение усилий в стержнях фермы.
|
|
Вначале проверяем ферму на наличие «нулевых» стержней. По лемме 1 в незагруженном узле 5 усилия в стержнях 5-6 и 5-4 равны нулю: S5-6=0; S5-4=0. По лемме 2 в незагруженном узле 3 усилие в стержне 3-8 равно нулю, а усилия в стержнях 2-3 и 3-4 равны, то есть: S3-8=0; S2-3=S3-4. Полученные значения усилий S5-4; S5-6; S3-8 заносим в итоговую таблицу 1.3.
Для определения усилий в стержнях методом «вырезания» пригодны узлы 1 и 6, так как в них сходятся по два стержня с неизвестными усилиями (в узле 6 из трёх стержней один S5-6=0).
Вырезаем узел 1 и изображаем схему действующих сил (рисунок 1.11).
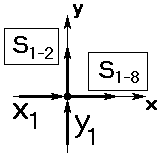
| Известными являются силы опорных реакций: Х1=7, 3 кН; У1=15, 8 кН. Неизвестными являются усилия в перерезанных стержнях: S1-2 и S1-8, которые для наглядности обводим прямоугольной рамкой. Определяем неизвестные усилия аналитически из уравнений равновесия: | |
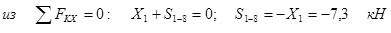 . .
| ||
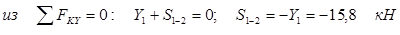 . .
| ||
| Отрицательные значения усилий указывают, что стержни 1-2 и 1-8 сжаты. Полученные значения S1-2 и S1-8 с учётом их знаков заносим в итоговую таблицу №1.3. | ||
| Рисунок 1.11. Схема сил узла 1 |
Вырезаем узел 2 и изображаем схему действующих сил (рисунок 1.12а).
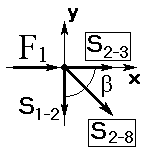
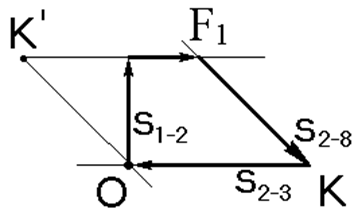
| Известными являются: внешняя сила F1 =10 кН и усилие в стержне S1-2 = =S2-1 = –15, 8 кН. Неизвестными являются усилия в перерезанных стержнях: S2-3 и S2-8. Определение неизвестных усилий произведём графическим способом. Для построения многоугольника сил примем масштаб: в 1 см 5 кН. Выберем произвольную точку О и отложим в масштабе от неё два вектора известных сил: S1-2 и F1, параллельно линиям действия этих сил и с учётом знаков. Вектор S1-2 (≈ 3, 1 см длиной) откладываем от точки О вверх и в конце этого вектора пристраиваем вектор F1 (2 см вправо). Затем из точки О и из конца вектора F1 проводим линии параллельно линиям действия S2-3 и S2-8 до их пересечений. Получилось две точки пересечений К и К’, которые равнозначны для образования замкнутого многоугольника сил. Примем для образования замкнутого многоугольника точку К. Тогда вектор S2-8 должен «войти» стрелкой в точку К, а вектор S2-3 «войти» стрелкой в точку О, чтобы получился замкнутый многоугольник сил с одинаковой ориентацией всех векторов (в данном случае – по часовой стрелке). Из направлений действия векторов видно, что S2-8 имеет положительное значение, а S2-3 – отрицательное | |
| Рисунок 1.12а Схема сил узла 2 | ||
| ||
| Рисунок 1.12б Многогранник сил узла 2 | ||
| (направлен к узлу). По результатам измерений получилось, что длина вектора S2-3 равна ≈ 5, 1 см, а длина вектора S2-8 – около 4, 5 см, что приближённо соответствует значениям сил: S2-3 = – 25, 5 кН, S2-8=22, 5 кН. Графический метод по сравнению с аналитическим является менее точным, поэтому полученные значения усилий подлежат проверке. |
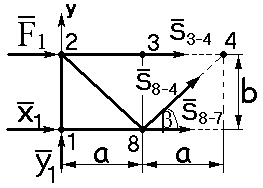
Метод Риттера применим для определения усилий в стержнях 3-4; 8-4; 8-7, для чего «рассечём» ферму по этим стержням и отбросим правую часть (рисунок 1.13).
Для определения усилий в стержне 3-4 необходимо составить уравнение моментов относительно точки 8, так как в ней пересекаются два других неизвестных усилия S4-8 и S7-8:
| 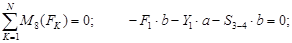 откуда откуда
| |
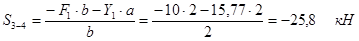 .
Следовательно, стержень 3-4 сжат.
Для определения усилия S8-4 составляем уравнения проекций на ось Y, перпендикулярную двум другим неизвестным усилиям S3-4 и S8-7: .
Следовательно, стержень 3-4 сжат.
Для определения усилия S8-4 составляем уравнения проекций на ось Y, перпендикулярную двум другим неизвестным усилиям S3-4 и S8-7:
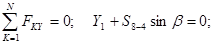 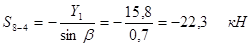 , то есть стержень 8-4 сжат. , то есть стержень 8-4 сжат.
| ||
| Рисунок 1.13. Левая часть рассечённой фермы |
Для нахождения усилия в стержне 8-7 следует составить уравнение моментов относительно точки 4, где пересекаются два других усилия S3-4 и S8-4: 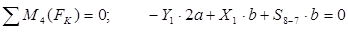 , откуда
, откуда
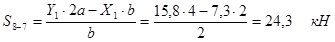 , ,
|
Полученные значения S3-4, S8-7 и S8-4 заносим в итоговую таблицу. При этом учтём, что согласно лемме 2 усилие S3-4 равно усилию S2-3. Поскольку значение S2-3 по графическому методу было равно –25, 5 кН, а по методу Риттера (более точному) получилось равным –25, 8 кН, то в итоговую таблицу заносим значения S2-3 = S3-4 = –25, 8 кН.
Вырезаем узел 8 и изображаем схему действующих сил (рисунок 1.14).
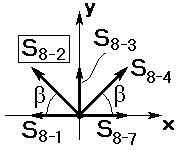
| По результатам предыдущих вычислений все силы в этом узле известны, однако значение S2-8=22, 5 кН определено графическим способом, поэтому нуждается в проверке. Для уточнения этого значения определим величину S2-8 аналитически из условия равновесия сил узла 8:
Из 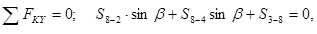 при S8-3= = 0 имеем S8-2 = –S8-4 = 22, 3 кН.
Ранее при графическом решении в узле 2 было получено S2-8 ≈ 22, 5 кН, поэтому за истинное значение принимаем S2-8 = =S8-2=22, 3 кН, полученное аналитически. при S8-3= = 0 имеем S8-2 = –S8-4 = 22, 3 кН.
Ранее при графическом решении в узле 2 было получено S2-8 ≈ 22, 5 кН, поэтому за истинное значение принимаем S2-8 = =S8-2=22, 3 кН, полученное аналитически.
| |
| Рисунок 1.14. Схема сил узла 8 | ||
| Вырезаем узел 7 и изображаем схему действующих сил (рисунок 1.15). | ||
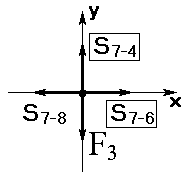
| Известными являются: внешняя сила F3=30 кН и усилие в стержне 7-8 S7-8 = 24, 3 кН. Неизвестными являются S7-6 и S7-4. Определим их значения аналитически из условий равновесия: | |
из 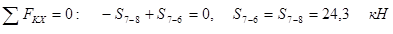 . .
| ||
из 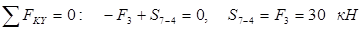 .
Полученные значения заносим в итоговую таблицу. .
Полученные значения заносим в итоговую таблицу.
| ||
| Рисунок 1.15. Схема сил узла 7 |
Вырезаем узел 4 и изображаем схему действующих сил (рисунок 1.16).
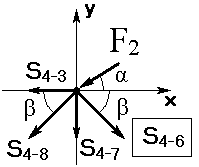
| Известными силами являются: внешняя сила F2=20 кН (или F2X=17, 3 кН; F2Y=10 кН). S3-4=–25, 8 кН; S4-8=–22, 3 кН; S4-7=30 кН; S4-5=0. Неизвестной является одна сила S4-6. | |||
| из | 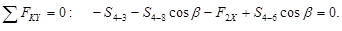
| |||
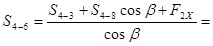
| ||||
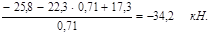
| ||||
| Полученное значение заносим в итоговую таблицу, в которой теперь содержаться значения усилий во всех стержнях. Для дополнительного контроля правильности определения усилий в стержнях фермы рассмотрим равновесие сил в узле 6. | ||||
| Рисунок 1.16. Схема сил узла 4 | ||||
Вырезаем узел 6 и изображаем схему действующих сил (рисунок 1.17).
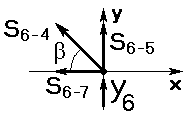
| Значения всех сил известны по результатам предыдущих вычислений, поэтому если усилия вычислены правильно, то уравнения равновесия должны обратиться в тождество типа 0=0:
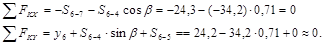 Следовательно, усилия в стержнях определены правильно.
Следовательно, усилия в стержнях определены правильно.
| |
| Рисунок 1.17. Схема сил узла 6 |