
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методика решения задач ЛП графическим методом
|
|
I. В ограничениях задачи (1.2) заменить знаки неравенств знаками точных равенств и построить соответствующие прямые.
II. Найти и заштриховать полуплоскости, разрешенные каждым из ограничений-неравенств задачи (1.2). Для этого нужно подставить в конкретное неравенство координаты какой-либо точки [например, (0; 0)], и проверить истинность полученного неравенства.
Если неравенство истинное,
то надо заштриховать полуплоскость, содержащую данную точку;
иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.
Поскольку 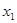 и
и 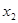 должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси
должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси 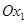 и правее оси
и правее оси 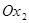 , т.е. в I-м квадранте.
, т.е. в I-м квадранте.
Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой. Поэтому необходимо выделить на графике такие прямые.
III. Определить ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделить ее. При отсутствии ОДР задача не имеет решений.
IV. Если ОДР – не пустое множество, то нужно построить целевую прямую, т.е. любую из линий уровня 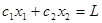 (где L – произвольное число, например, кратное
(где L – произвольное число, например, кратное 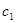 и
и 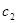 , т.е. удобное для проведения расчетов). Способ построения аналогичен построению прямых ограничений.
, т.е. удобное для проведения расчетов). Способ построения аналогичен построению прямых ограничений.
V. Построить вектор 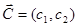 , который начинается в точке (0; 0) и заканчивается в точке
, который начинается в точке (0; 0) и заканчивается в точке 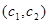 . Если целевая прямая и вектор
. Если целевая прямая и вектор 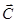 построены верно, то они будут перпендикулярны.
построены верно, то они будут перпендикулярны.
VI. При поиске максимума ЦФ необходимо передвигать целевую прямую в направлении вектора 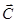 , при поиске минимума ЦФ – против направления вектора
, при поиске минимума ЦФ – против направления вектора 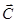 . Последняя по ходу движения вершина ОДР будет точкой максимума или минимума ЦФ. Если такой точки (точек) не существует, то можно сделать вывод о неограниченности ЦФ на множестве планов сверху (при поиске максимума) или снизу (при поиске минимум).
. Последняя по ходу движения вершина ОДР будет точкой максимума или минимума ЦФ. Если такой точки (точек) не существует, то можно сделать вывод о неограниченности ЦФ на множестве планов сверху (при поиске максимума) или снизу (при поиске минимум).
VII. Определить координаты точки max (min) ЦФ 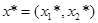 и вычислить значение ЦФ
и вычислить значение ЦФ 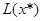 . Для вычисления координат оптимальной точки
. Для вычисления координат оптимальной точки 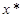 необходимо решить систему уравнений прямых, на пересечении которых находится
необходимо решить систему уравнений прямых, на пересечении которых находится 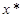 .
.
1.3 Особые случаи решения задач линейного программирования
Для выработки наглядных представлений о ЗЛП рассмотрим графический метод, который может быть применен в случае решения ЗЛП с двумя переменными:
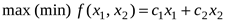
| (7.1) |
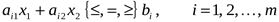 , ,
| (7.2) |
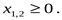
| (7.3) |
где 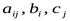 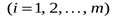 , , 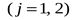 – заданные постоянные величины. – заданные постоянные величины.
|
Геометрически ЗЛП представляет собой отыскание в многоугольнике решений такой угловой точки, координаты которой дают максимальное (минимальное) значение линейной целевой функции, причем допустимыми решениями являются все точки многоугольника решений.
Алгоритм решения ЗЛП с двумя переменными графическим методом.
Построить область допустимых решений (ОДР) ЗЛП.
1. Построить вектор-градиент целевой функции 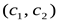 , перпендикулярно ему провести прямую (линию уровня).
, перпендикулярно ему провести прямую (линию уровня).
2. Перемещать линию уровня в направлении вектора-градиента при решении задачи на max, в обратном направлении – при решении задачи на min.
3. Последняя точка области при этом движении и является точкой оптимального решения.
Возможны следующие особые случаи:
1. Линия уровня параллельна некоторой стороне многоугольника (ОДР). В этом случае каждая угловая точка этой стороны многоугольника и любая точка между ними является оптимальным решением ЗЛП (бесконечное множество решений).
2. ОДР является неограниченной, целевая функция на ОДР не ограничена сверху (задача на max не имеет решения).
3. Система ограничений несовместима, ОДР есть пустое множество (ЗЛП не имеет решения).
ЗАДАЧИ
Предприятие осуществляет выпуск комплектующих изделий А и В, для производства которых используются сталь и цветные металлы. Технологический процесс предполагает обработку изделий на токарных и фрезерных станках. Технологическими нормами производства изделий предусмотрены определенные затраты сырья (кг) и времени (станко-час). Технологические данные производственного процесса представлены в таблице. В течение месяца предприятие располагает ограниченными ресурсами сырья и времени обработки изделий в производственных цехах. Прибыль от реализации изделия А составляет 70 руб./шт., изделия В — 180 руб./шт.
| Продукция/ Ресурсы | Сырье, кг | Обработка, станко-час | Прибыль, руб. | ||
| Цветные металлы | Сталь | Токарные работы | Фрезерные работы | ||
| Изделие А | |||||
| Изделие В | |||||
| Ресурсы |
1.Найдите оптимальный план производства (количество изделий А и В), дающий наибольшую прибыль.
2. Проведите анализ решения с использованием двойственных оценок.
Экономико-математическая модель задачи:
Переменные: 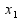 -изделие А;
-изделие А; 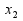 - изделие В.
- изделие В.
Целевая функция: f (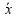 ) = 60
) = 60 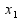 +160
+160 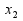
 max
max
Ограничения:
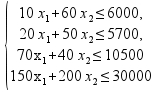
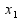 ,
, 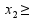 0
0
1. Строим ОДР ЗЛП:
 : : 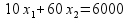
| 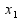
| 0 | 600 |
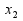
| 100 | 0 | |
 : : 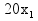 + + 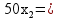 5700 5700
| 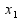
| 0 | 285 |
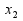
| 114 | 0 | |
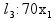 +40 +40 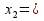 10500 10500
| 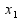
| 0 | 150 |
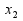
| 262, 5 | 0 | |
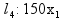 +200 +200 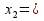 30000 30000
| 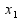
| 0 | 200 |
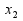
| 150 | 0 |
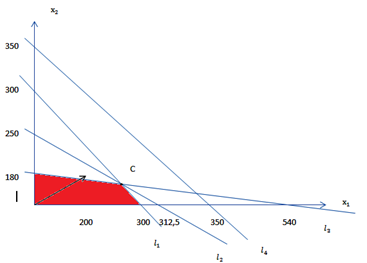
В результате пересечения построенных четырех полуплоскостей получаем многоугольник, который и является областью допустимых решений нашей задачи. Любая точка этого многоугольника удовлетворяет всем четырем функциональным неравенствам, а для любой точки вне этого многоугольника хотя бы одно неравенство будет нарушено.
2. Для определения направления движения к оптимуму построим вектор-градиент 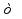 , координаты которого являются частными произведениями целевой функции:
, координаты которого являются частными произведениями целевой функции:
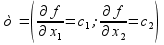 =
= 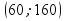
Чтобы построить такой вектор, нужно соединить точку (60; 160) с началом координат.
3. Строим линию уровня, которая является перпендикуляром вектора градиента.
4. Далее будем передвигать линию уровня до ее выхода из ОДР. При максимизации целевой функции движение линии уровня будем осуществлять по направлению градиента. В точке С достигается max целев. функции. Для нахождения координат этой точки решим систему из уравнений двух прямых, дающих в пересечении точку максимума:
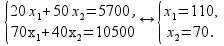
Получаем 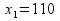 и
и 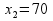 . При этих значениях max f (
. При этих значениях max f ( ) = 60
) = 60 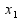 +160
+160 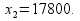
Вывод: для получения max прибыли (17800) необходимо 110 шт изделия А (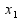 =110) и 70 шт изделия В (
=110) и 70 шт изделия В (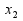 =70).
=70).
Сформулируем двойственную задачу и найдем двойственные оценки.
Целевая функция: g (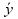 ) = 6000
) = 6000 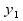 +5700
+5700 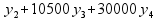
 min
min
Ограничения:
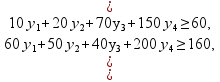
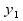 ,
, 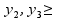 0
0
Найдем оптимальный план двойственной задачи, используя теоремы двойственности.
Воспользуемся первым соотношением второй теоремы двойственности:
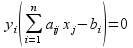
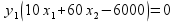
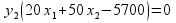
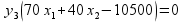
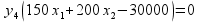
Подставим оптимальные значения вектора х в полученное выражение:

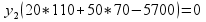
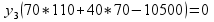
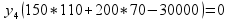
Получим:
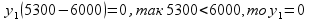
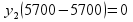
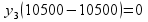
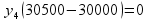 ,
,
так 30500> 30000, то 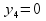
Воспользуемся вторым соотношением второй теоремы двойственности:
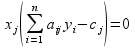
Если 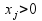 , то
, то 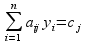
В нашей задаче Х1=110 > 0 и Х2=70> 0, поэтому первое и второе ограничения двойственной задачи обращаются в равенства:
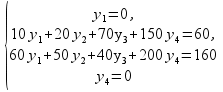
Решив систему уравнений, получим: 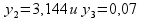
Проверим выполнение первой теоремы двойственности:
g (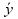 ) = 6000
) = 6000 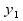 +5700
+5700 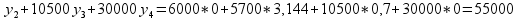
f (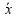 ) = 60
) = 60 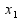 +160
+160 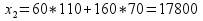
Оптимальный план двойственной задачи определен, верно.
Проанализируем использование ресурсов в оптимальном плане.
Если 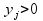 , то
, то 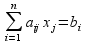
Если 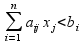 , то
, то 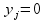
Необходимый запас сырья по изделию А и В имеют отличные от нуля оценки 2 и 3- они полностью используются в оптимальном плане, являются дефицитными, сдерживающими рост целевой функции. Правые части этих ограничений равны левым
Необходимый фонд рабочего времени токарных работ используется не полностью 53000< 6000, поэтому имеет нулевую двойственную оценку 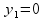 . Этот ресурс не влияет на план получения прибыли.
. Этот ресурс не влияет на план получения прибыли.
Необходимый фонд рабочего времени фрезерных работ используется не полностью 35000> 30000, поэтому имеет нулевую двойственную оценку 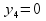 . Этот ресурс не влияет на план получения прибыли
. Этот ресурс не влияет на план получения прибыли
Общая прибыль изготовления изделия А 110 и В 70составит 17800 руб
Решение в MS EXCEL:
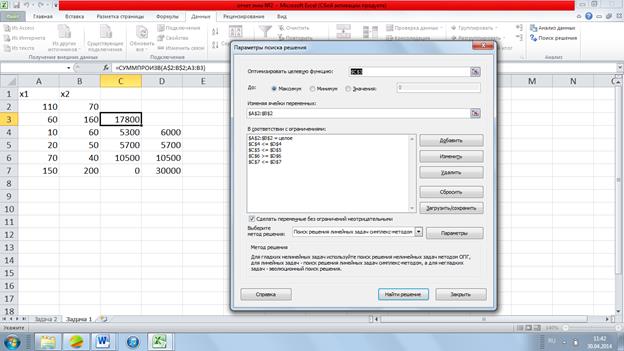
 Ответ: Получаем
Ответ: Получаем 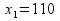 и
и 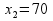 . При этих значениях max f (
. При этих значениях max f (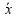 ) = 60
) = 60 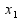 +160
+160 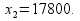
В течение девяти последовательных недель фиксировался спрос Y(t) (млн. руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен в таблице.
| № наблюдения | ||||||||
Требуется определить:
1. 1. Проверьте наличие аномальных наблюдений.
2. 2. Постройте линейную модель 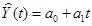 , параметры которой оцените МНК.
, параметры которой оцените МНК.
3. 3. Оценить адекватность построенной модели, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S - критерия возьмите табулированные границы 2, 7 – 3, 7).
1. 4. Оцените точность моделей на основе использования средней относительной ошибки аппроксимации.
2. 5. Осуществите прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитайте при доверительной вероятности р =70%).
3. 6. Фактические значения показателя, результаты моделирования и прогнозирования представьте графически.