
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Векторная алгебра.
|
|
«Элементы векторной алгебры»
1. Векторы и простейшие действия над ними.
2. Скалярное и векторное произведения, смешанное произведение.
§3.1. Векторы и простейшие действия над ними.
Величины, рассматриваемые в механике, физике, электротехнике и др. дисциплинах, делятся на векторные и скалярные. Величины, определяемые только своим численным значением – скалярные. (длина, масса, плотность, объём, время, температура, любое вещественное число – скаляры.)
Величины, определяемые не только своим численным значением, но и направлением в пространстве, называются векторами. (сила, скорость, ускорение, напряженность электрического и магнитного полей)
Определение 1. Вектор – направленный отрезок.
Длину вектора будем называть модулем вектора обозначать 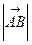 . Вектор, длина которого равна нулю, называется нулевым вектором
. Вектор, длина которого равна нулю, называется нулевым вектором 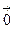

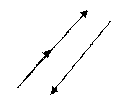
Определение 2. Два вектора называются коллинеарными, если их направления совпадают или противоположны.
Нулевой вектор считается коллинеарным любому вектору.
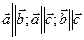
Определение 3. Два вектора называются равными если:
а) они соноправлены
б) имеют равные длины 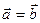
Определение 4. Векторы называются компланарными, если существует плоскость, которой они параллельны.