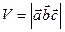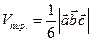Скалярное и векторное произведение векторов.

Определение. Скалярным произведением двух векторов называется число, равное произведению их модулей на косинус угла между векторами.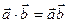

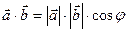
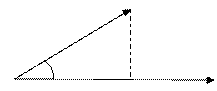Спроектируем вектор 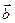на 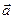Получим 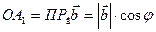, тогда 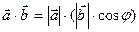= 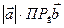аналогично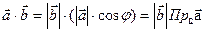

Значит, 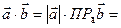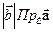, т.е скалярное произведение двух векторов равно модулю одного из векторов, умноженному на проекцию второго вектора на первый.

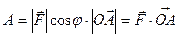
Пример.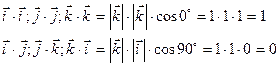

Скалярное произведение одноименных орт равно 1, разноименных равно 0.

Основные свойства скалярного произведения

1. Переместительное свойство: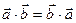

2. Распределительное свойство: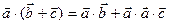

3. Сочетательное свойство относительно числового множителя:

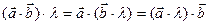
4. Скалярное произведение обращается нуль в том и только том случае, когда векторы перпендикулярны: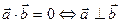

5. Так как модуль вектора, число неотрицательное, то знак скалярного произведения определяется знаком cos :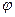

а) если 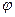- острый угол, то 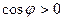и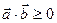

б) если 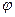- тупой угол, то 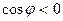и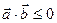

Умножение векторов в координатах.

Даны векторы: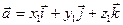

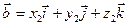
Найдём: ()()=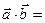

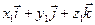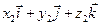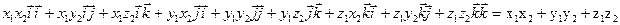
Приложения скалярного произведения

1. Длина вектора. 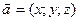Найти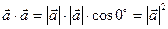

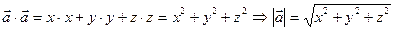
2. Расстояние между точками. ,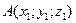

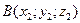
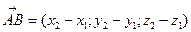
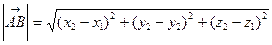
3. Угол между векторами.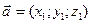

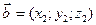
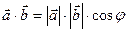
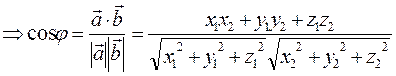
4. Проекция одного вектора на другой.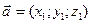

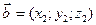
Найти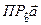

=

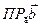
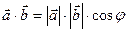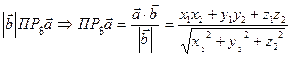
5. Условие перпендикулярности векторов.

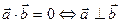
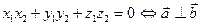
Векторное произведение векторов.

Определение. Векторным произведением двух векторов 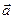и 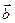называется такой третий вектор 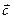, модуль которого численно равен площади параллелограмма, построенного на векторах 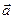и 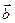, перпендикулярный плоскости, определяемой векторам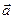и и 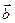, и направленный в такую сторону, что кратчайший поворот от 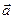к 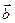вокруг вектора 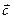представляется происходящим против часовой стрелки, если смотреть из конца вектора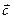

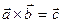
1.

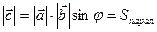
2.

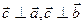
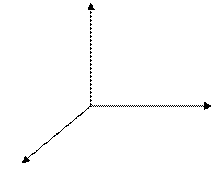
3. Вектор 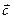направлен так, что поворот от вектора 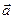к вектору 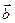вокруг вектора 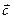происходит против часовой стрелки, если смотреть из конца вектора .

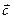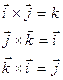
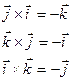
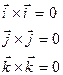
Свойства векторного произведения.

1.

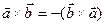
2. 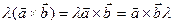(сочетательный закон)

3. (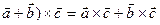 (распределительный закон)

4. ║

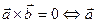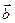
Векторное умножение векторов в координатах.

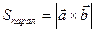
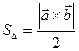
§3.6 Смешанное произведение векторов.

Определение. Смешанным произведением векторов 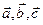называется скалярное произведение векторов 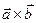на вектор 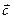, т.е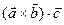

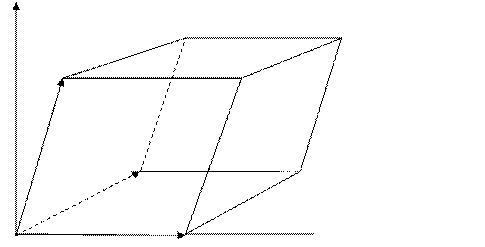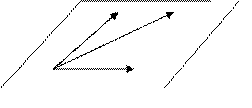
Смешанное произведение трех векторов 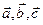по модулю равно объёму параллелепипеда, построенного на этих векторах.

Свойства смешанного произведения.

1. Смешанное произведение равно нулю если:

- хоть один из перемножаемых векторов равен нулю.

- два из перемножаемых векторов коллинеарны.

- три ненулевых вектора параллельны одной и той же плоскости (компланарность)

2. Смешанное произведение не изменится, если в нем поменять местами знаки векторного 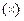и скалярного умножения.

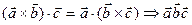
3. Смешанное произведение не изменится, если переставлять перемножаемые векторы в круговом порядке.

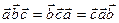
4. При перестановке любых двух векторов смешанное произведение меняет только знак:

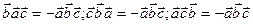
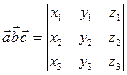
Необходимым и достаточным условием компланарности трех векторов служит условие 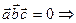уравнение плоскости