Дифференциальное исчисление функций нескольких переменных

Контрольная работа №1

Задача 1. Найти и изобразить область определения следующей функции: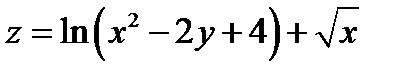

Решение:

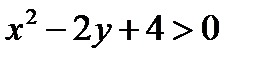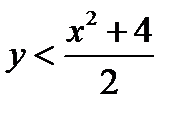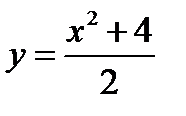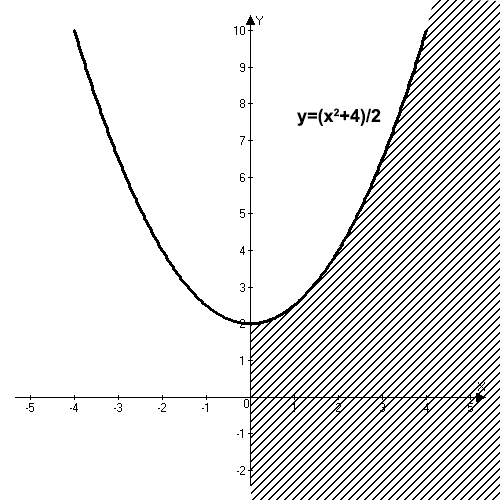
Логарифмическая функция определена только при положительном значении аргумента, поэтому , или . Значит границей области определения будет парабола . Кроме того подкоренное выражение должно быть неотрицательным, т.е. 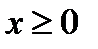. Таким образом, область определения функции состоит из точек, расположенных ниже параболы 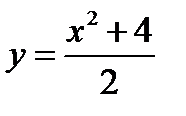и справа от оси OY, включая точки на оси OY.

Задача 2. Проверить, удовлетворяет ли функция 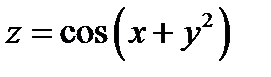уравнению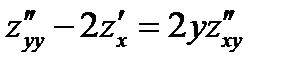

Решение:

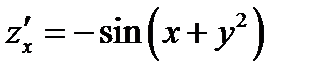
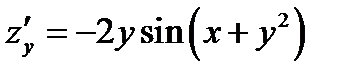
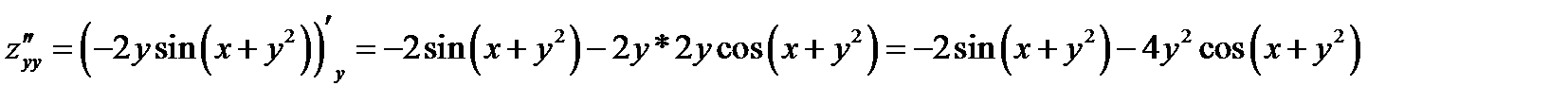
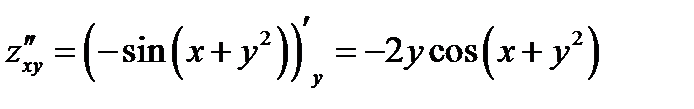
Подставляем найденные производные в уравнение

Левая и правая части уравнения равны, значит функция 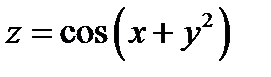удовлетворяет уравнению .

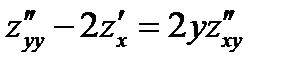Задача 3. Найти производные , 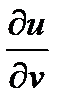сложной функции , ,

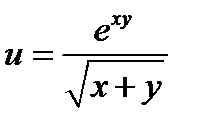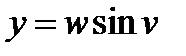
Решение:

; ; ; ; ;

;

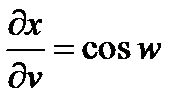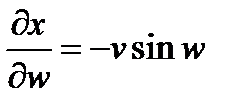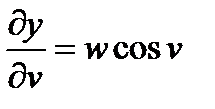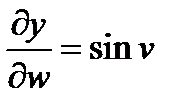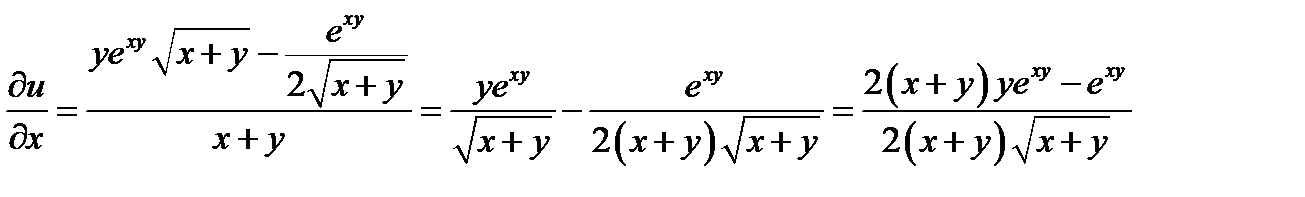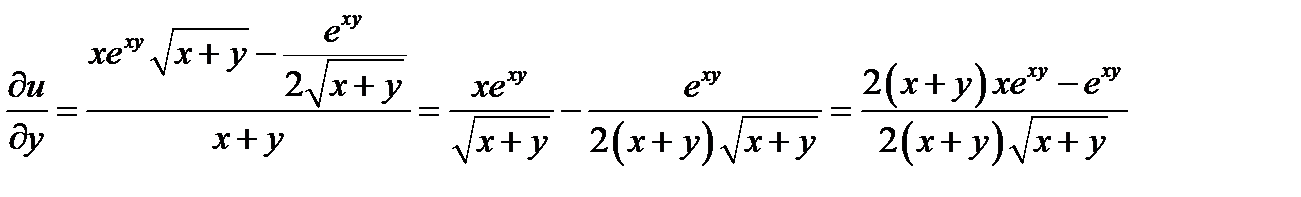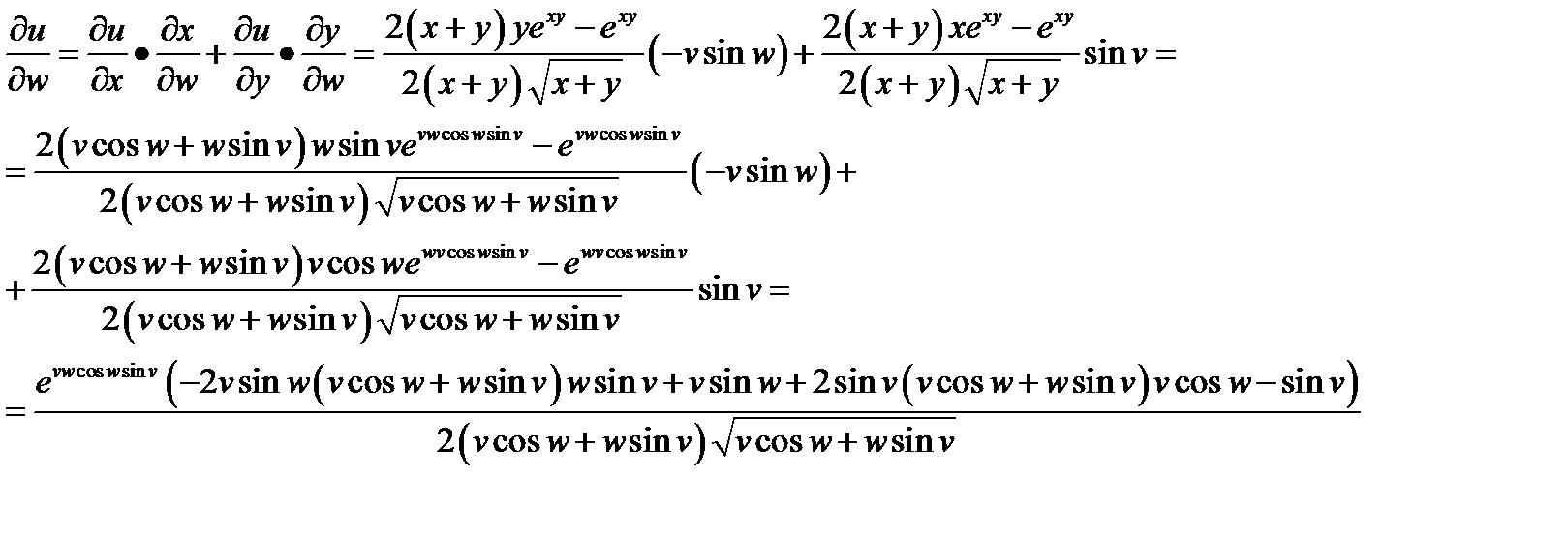
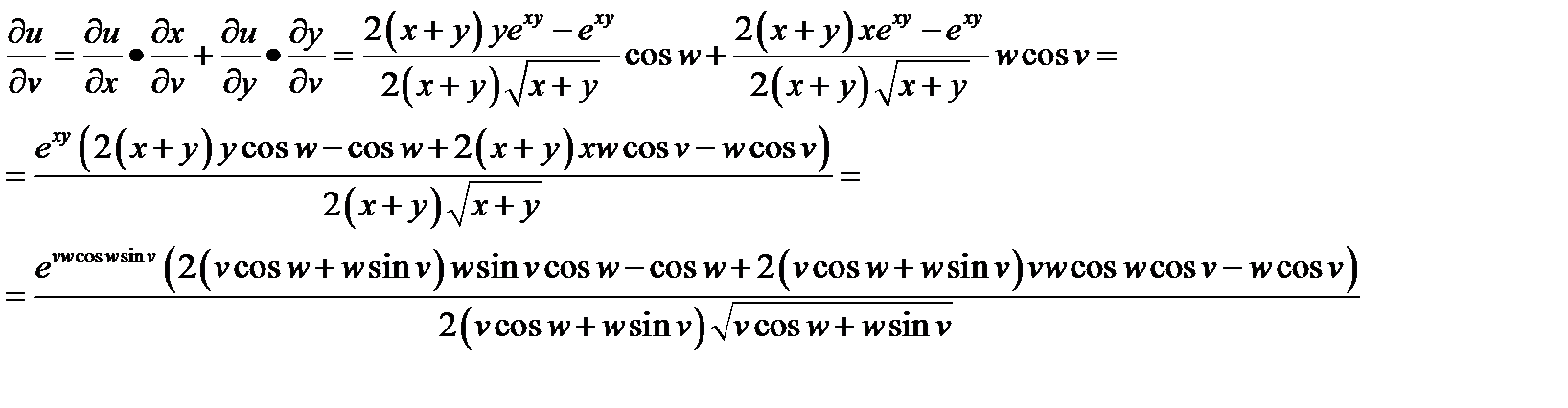
Задача 4. Найти первые производные неявной функции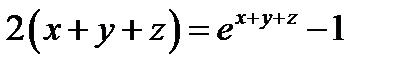

Решение:

; ;

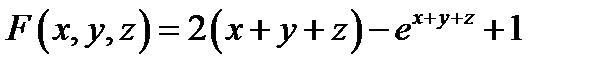
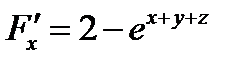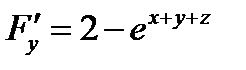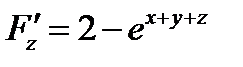
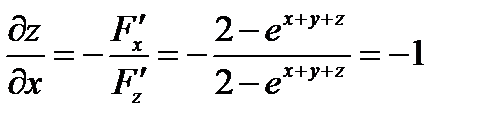
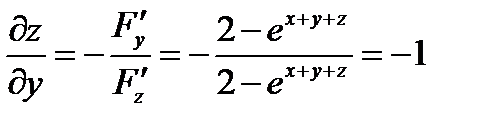
Задача 5. Найти дифференциалы второго порядка 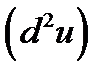следующей функции 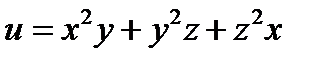(x, y, z – независимые переменные)

Решение:

; ; ;

; ; ;

; ; ;

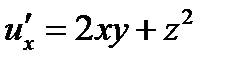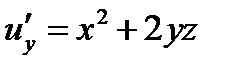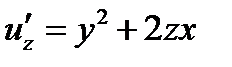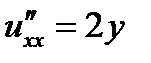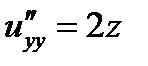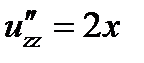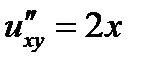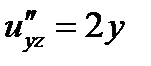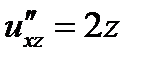Задача 6. Вычислить приближенное значение функции 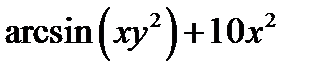в точке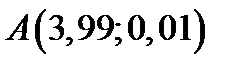

Решение:

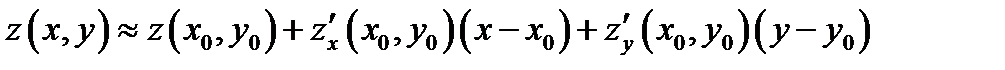
Имеем 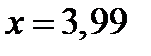, 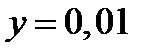. Положим 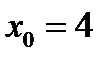, 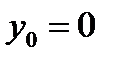. Отсюда

; ;

;

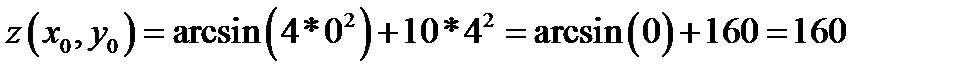
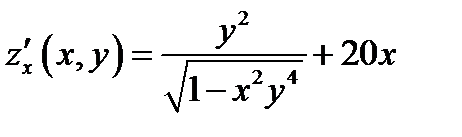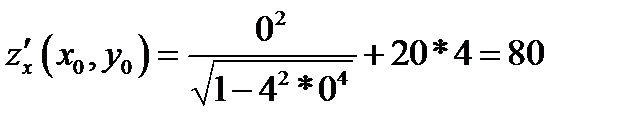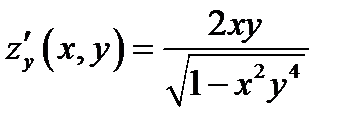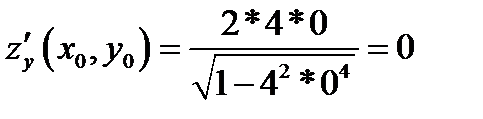
значит

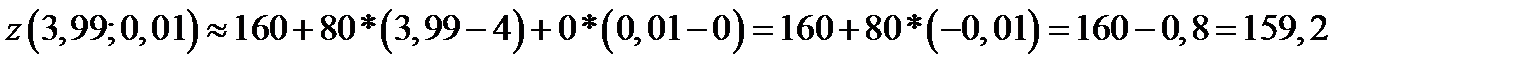
Задача 7. Разложить функцию 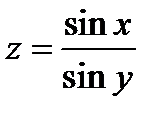по формуле Тейлора в точке 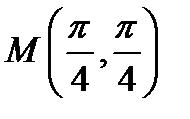, ограничиваясь членами второго порядка включительно

Решение:

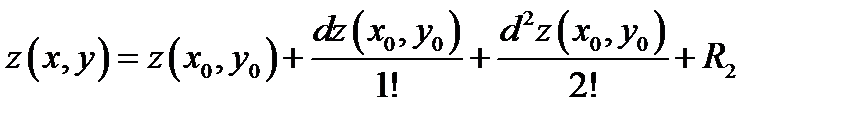; где 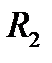– остаточный член формулы Тейлора.

; ; ; ; ; ;

;

; ;

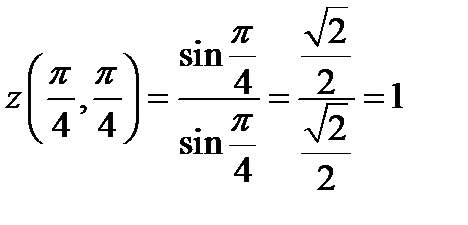
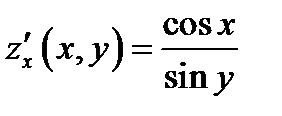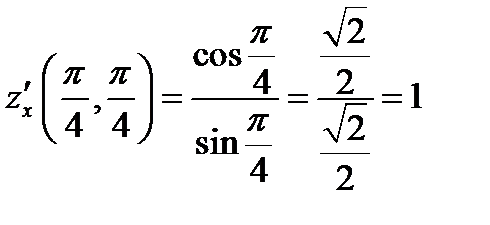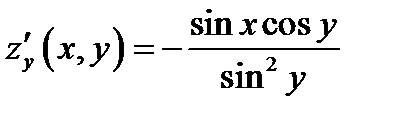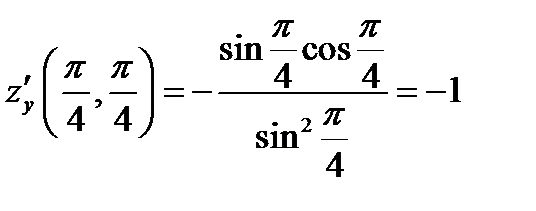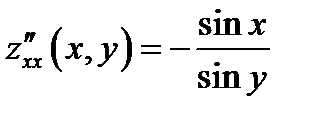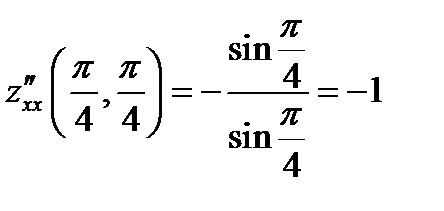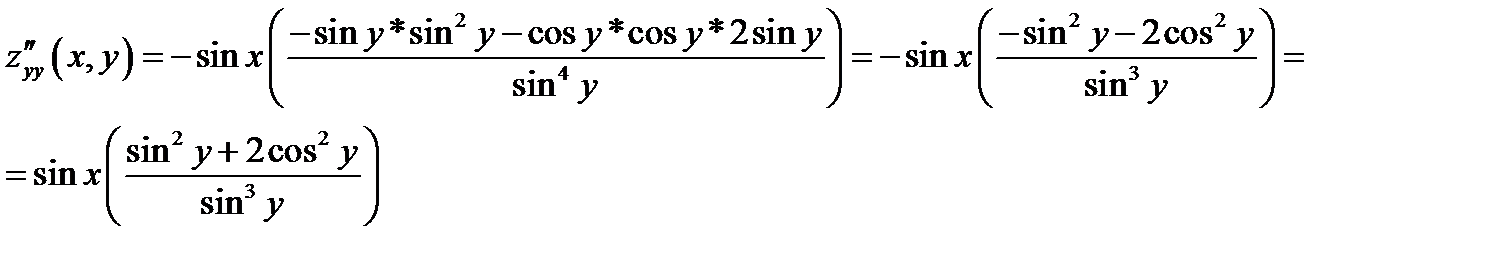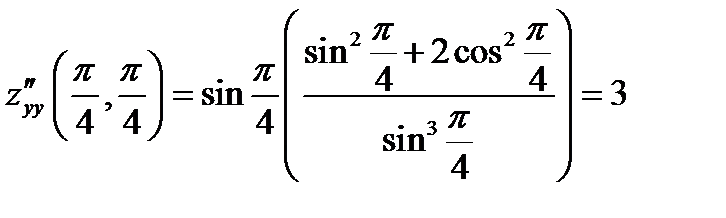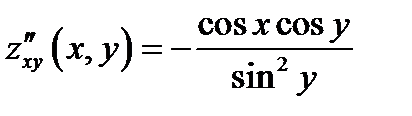дифференциалы будут равны

;

,

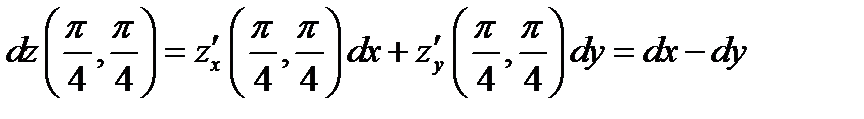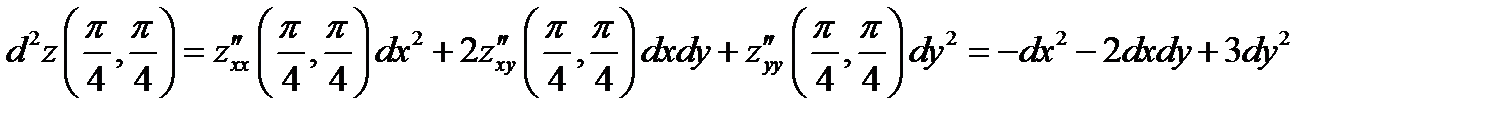учитывая, что 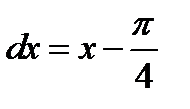, , 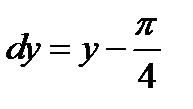получим

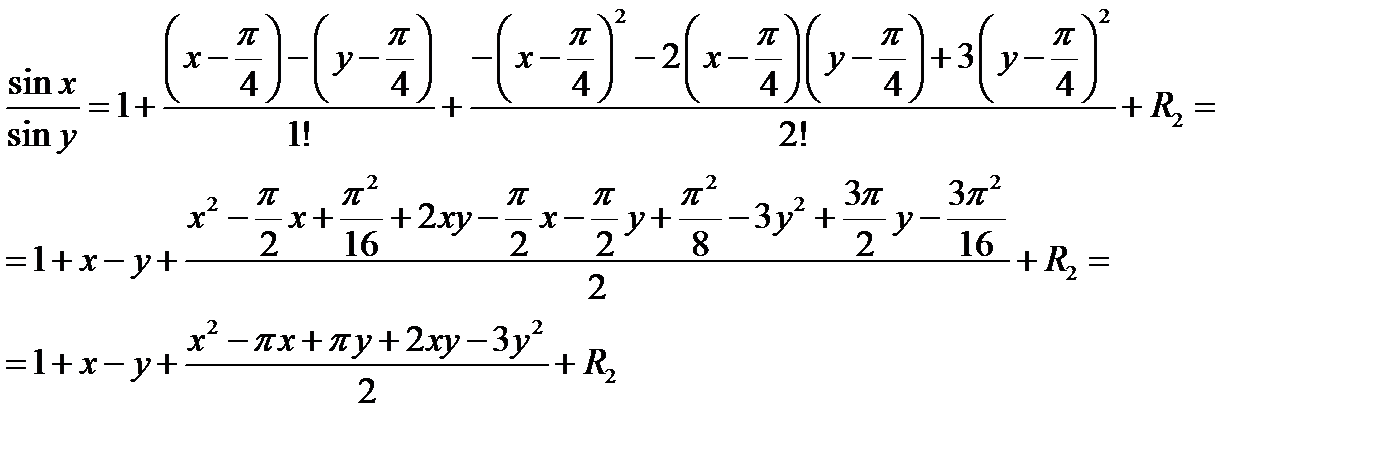
Задача 8. Составить уравнения касательной плоскости и нормали к поверхности 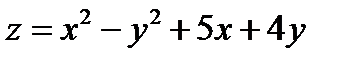в точке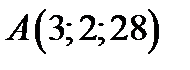

Решение:

Уравнение касательной плоскости в точке 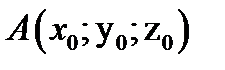имеет вид ,

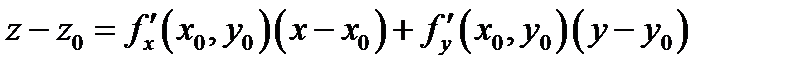а уравнение нормали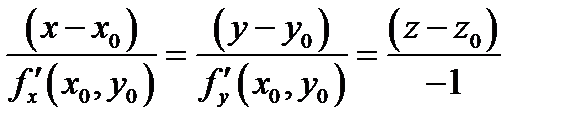

Находим значения частных производных

, , ,

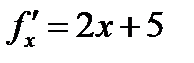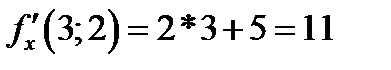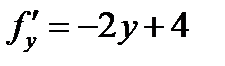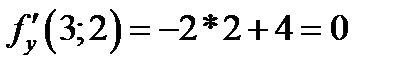
отсюда уравнение касательной плоскости будет иметь вид

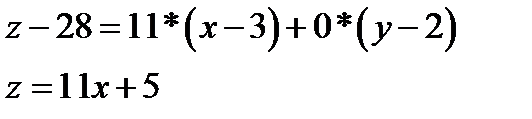
уравнение нормали

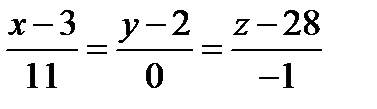
Задача 9. Дана функция 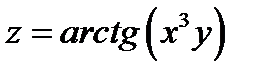, точка 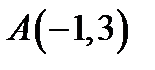и вектор 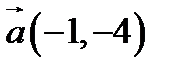. Найти:

1) grad z в точке A;

2) производную в точке A по направлению вектора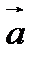

Решение:

,

,

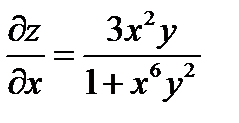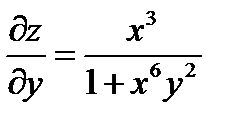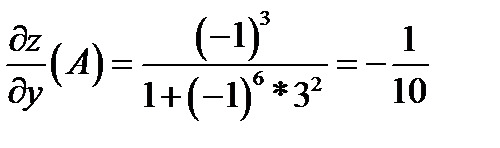
Таким образом

Находим единичный вектор

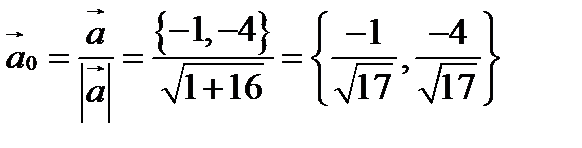
Тогда производная в точке A по направлению вектора 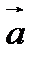будет равна

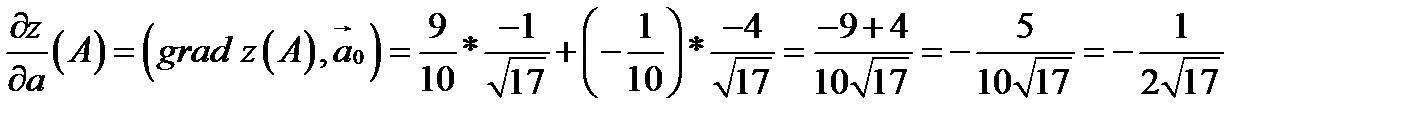
Задача 10. Найти экстремумы функции двух переменных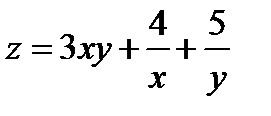

Решение:

Найдем стационарные точки

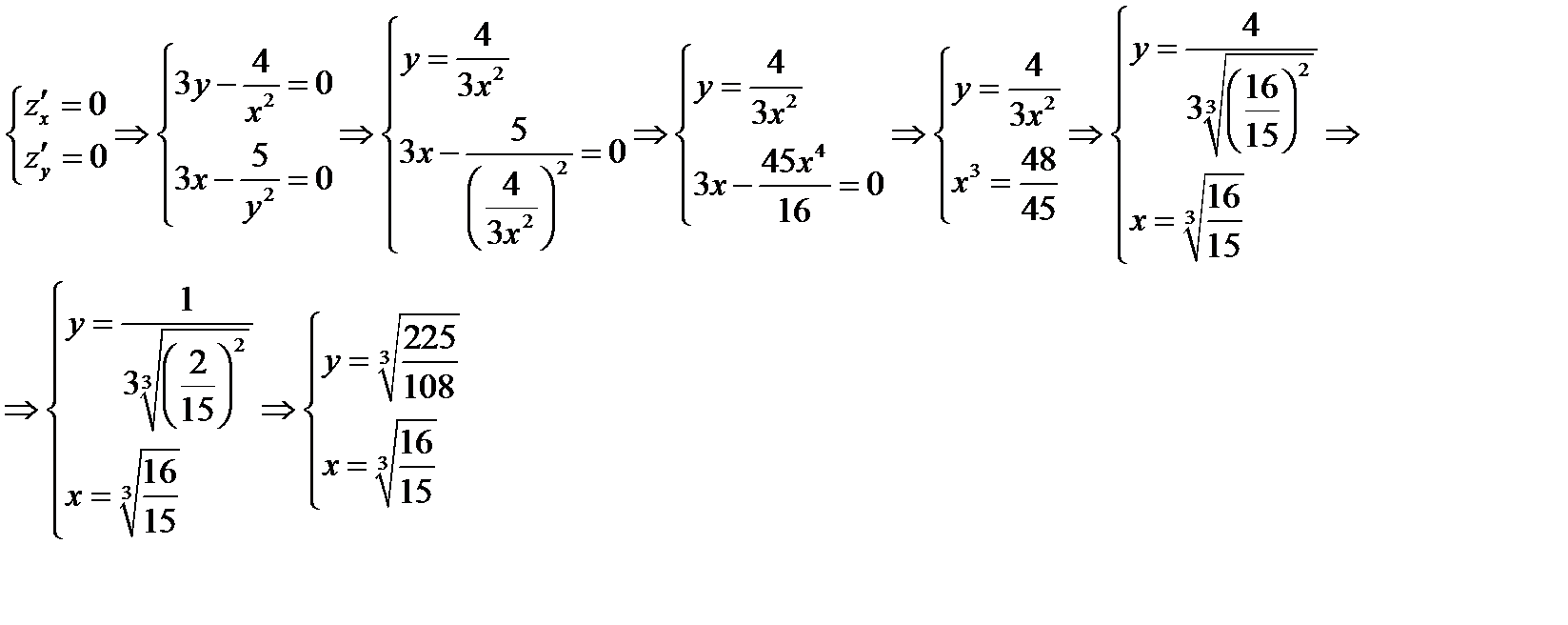
В точке 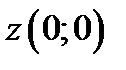функция 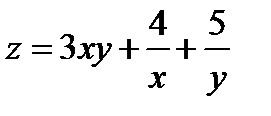не существует, таким образом получаем одну стационарную точку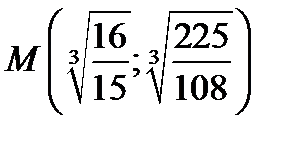

Находим

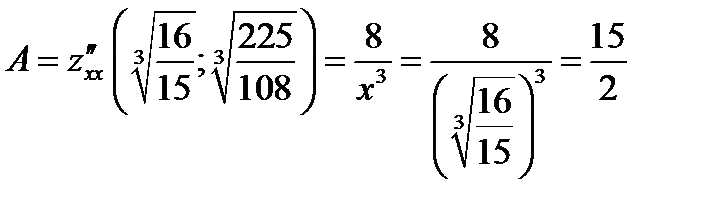
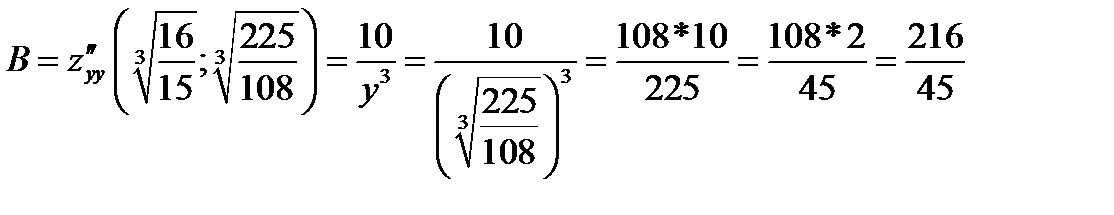
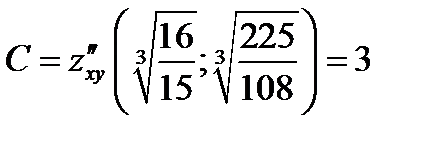
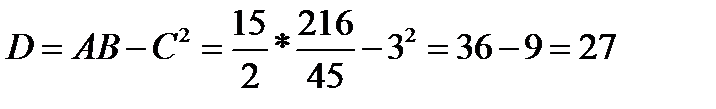
Так как 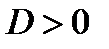и 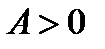, то точка 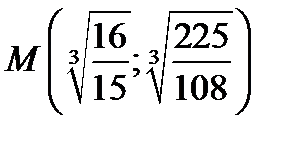является точкой экстремума, а именно минимума.

Найдем минимум функции

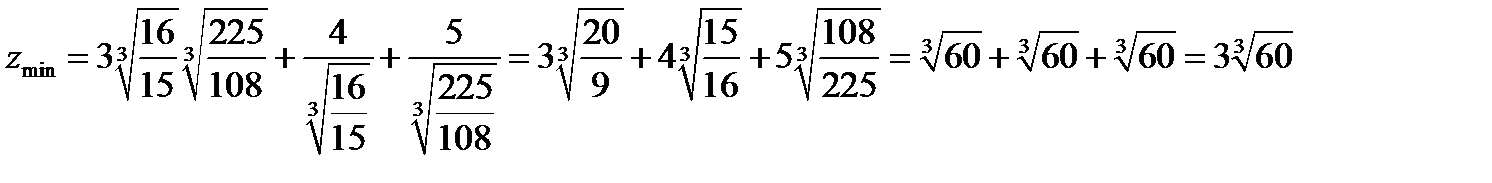
Задача 11. Найти экстремумы функции трех переменных

Решение:

Найдем стационарные точки

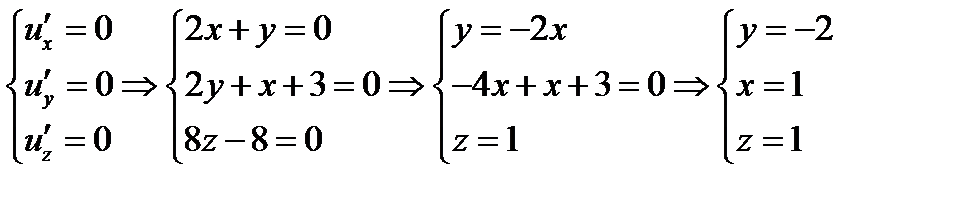
Таким образом получаем одну стационарную точку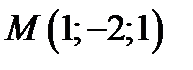

Найдем частные производные второго порядка и вычислим их значения в стационарной точке

; ; ; ; ;

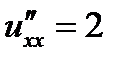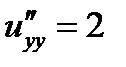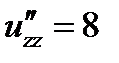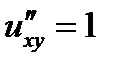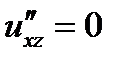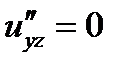
Найдем дифференциал второго порядка

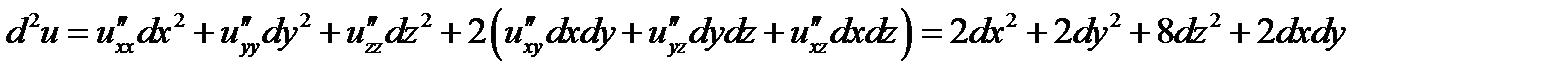
Воспользуемся критерием Сильвестра

; ;

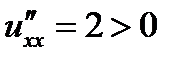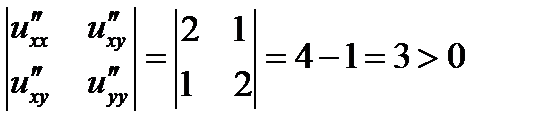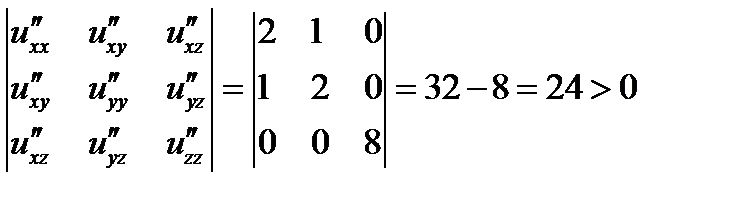
Согласно критерию Сильвестра 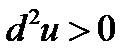. Значит, точка 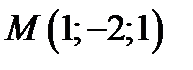является точкой минимума функции . Значение функции в точке минимума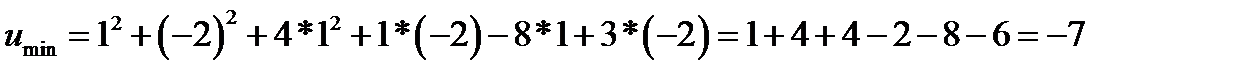

Задача 12. Найти условный экстремум функции 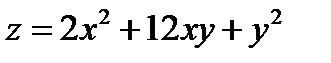при уравнении связи 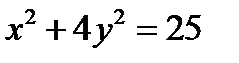, (x > 0)

Решение:

Составляем функцию Лагранжа:

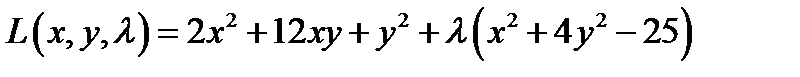
Находим точки, в которых возможен условный экстремум

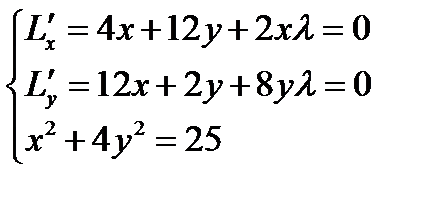
Рассмотрим одновременно два первых уравнения системы в виде

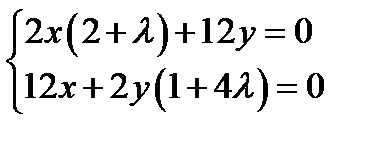
Если решать эту систему относительно переменных 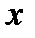и 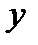, то, применяя правило Крамера, получим следующее: если главный определитель системы отличен от нуля, то система имеет единственное решение 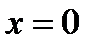, 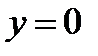. Однако это решение противоречит третьему уравнению исходной системы. Поэтому единственная возможность получить ненулевые решения системы из двух первых уравнений – это приравнять главный определитель системы из двух уравнений нулю:

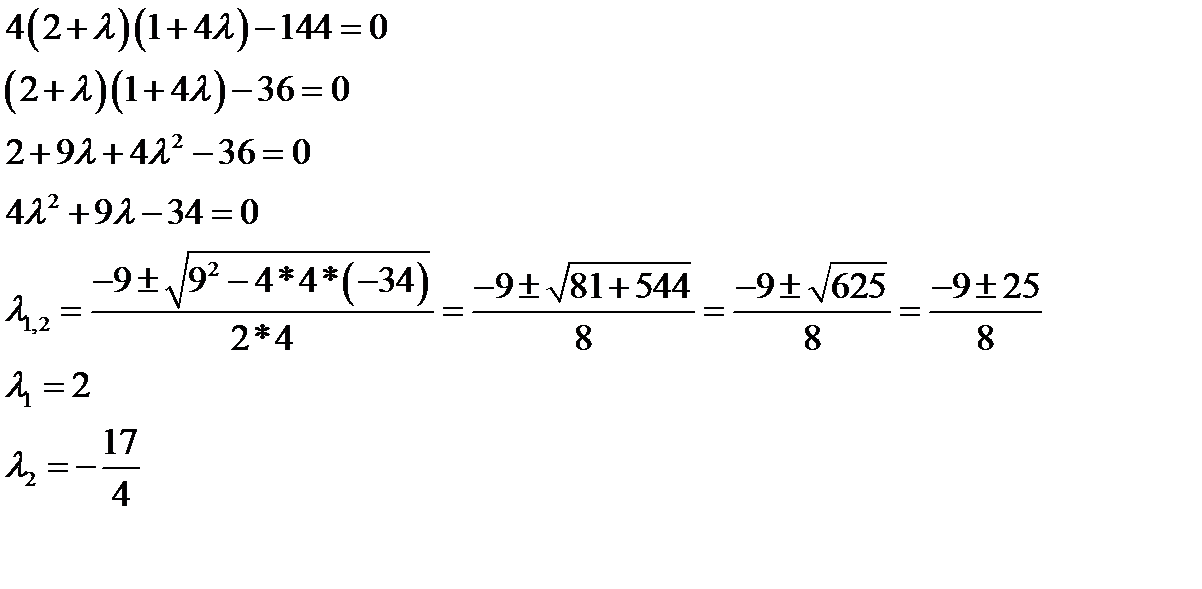
При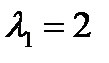

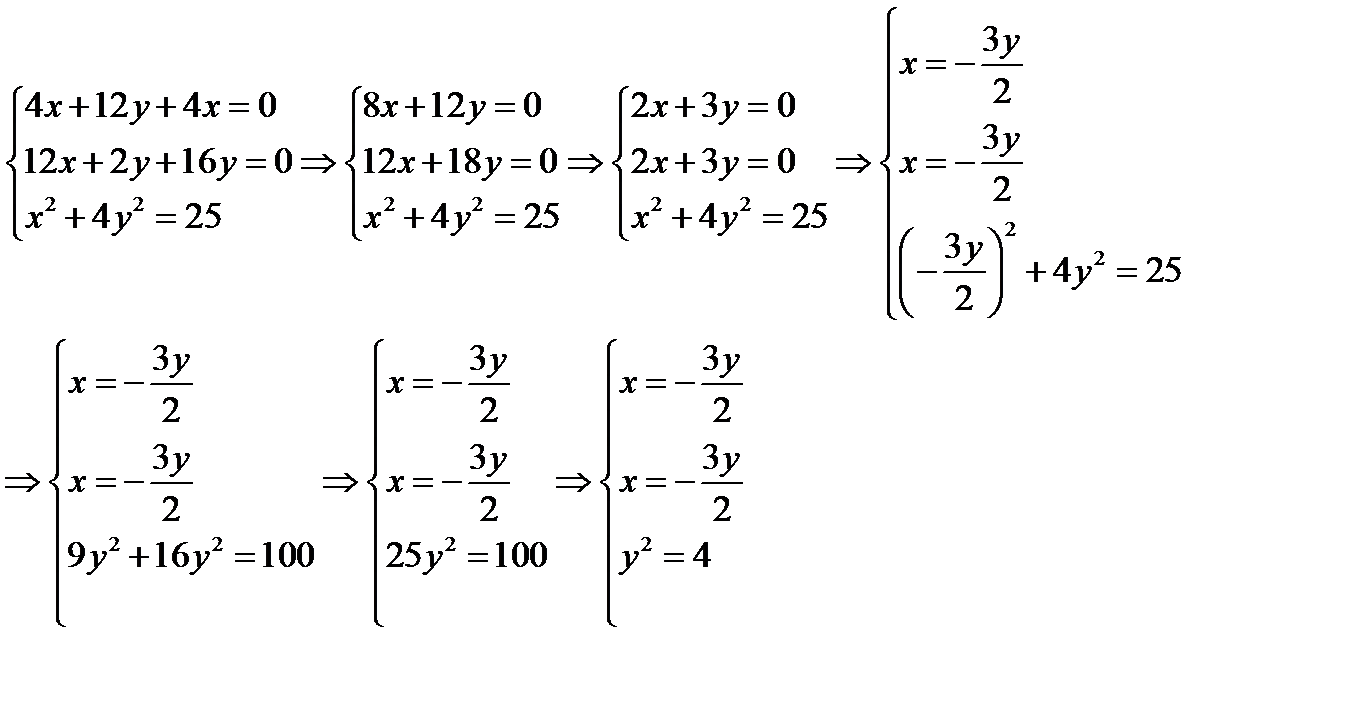
Таким образом получаем критические точк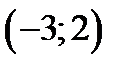и и 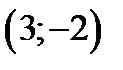. Значение функции в этих точках .

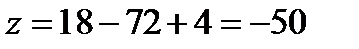При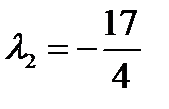

Таким образом получаем критические точк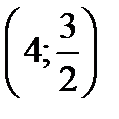и и 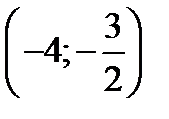. Значение функции в этих точках .

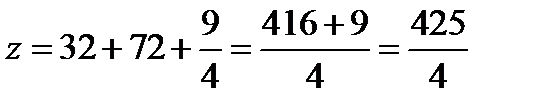Таким образом, условным минимумом исходной функции является значение 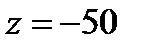, а условным максимумом является значение .

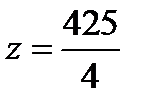Задача 13. Найти наименьшее и наибольшее значение функции 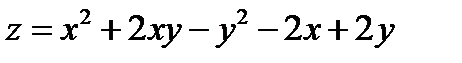в замкнутой области D, заданной системой неравенств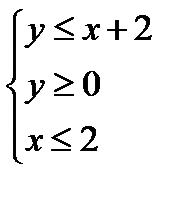

Решение:

Построим область D

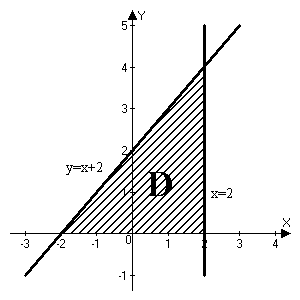
Найдем стационарные точки внутри области D

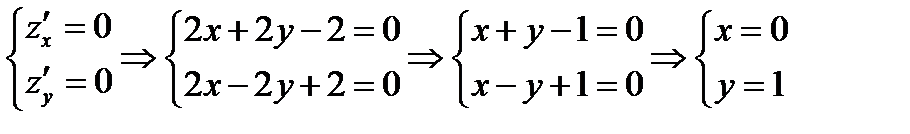
Стационарная точка 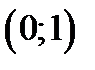принадлежит области D,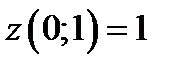

Исследуем границы области D.

Граница 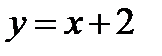. На этой границе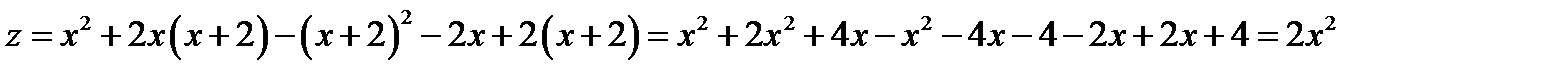

Таким образом наибольшее и наименьшее значение функции z на границе 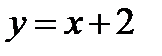находятся в точках 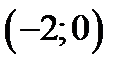, , 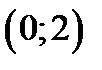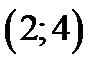. Находим , , .

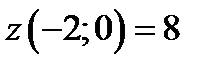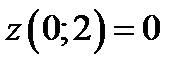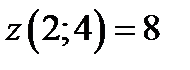Граница . На этой границе 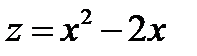. . 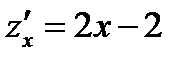Из уравнения 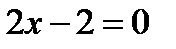получаем 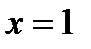. Таким образом наибольшее и наименьшее значение функции z на границе 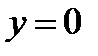находятся в точках 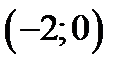, , 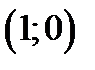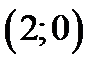. Находим , .

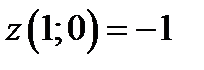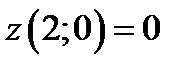Граница 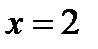. На этой границе 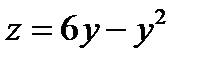. . 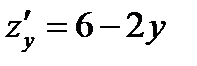Из уравнения 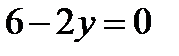получаем 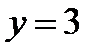. Таким образом наибольшее и наименьшее значение функции z на границе 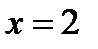находятся в точках 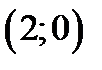, , 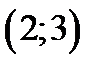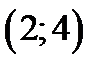. Находим .

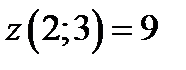Сравнивая полученные значения 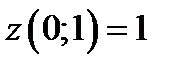, , 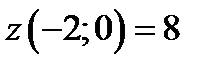, , 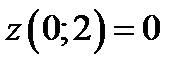, , 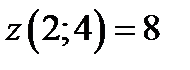, 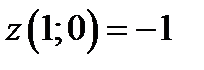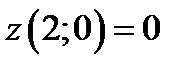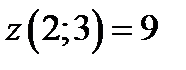заключаем, что наибольшее и наименьшее значения функции в области D равны соответственно и .

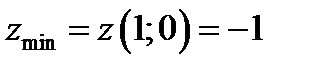Задача 14. Экспериментально получены пять значений функции 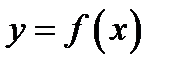при пяти значениях аргумента x, которые записаны в таблице. Методом наименьших квадратов найти функцию вида 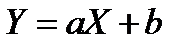, выражающую приближенно (аппроксимирующую) функцию 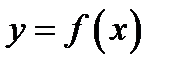. Сделать чертеж, на котором в декартовой прямоугольной системе координат изобразить экспериментальные точки и график аппроксимирующей функции .

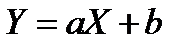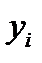
	3, 8	4, 8	3, 5	2, 9	1, 5

Решение:

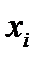
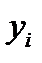
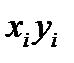
		3, 8		3, 8
		4, 8		9, 6
		3, 5		10, 5
		2, 9		11, 6
		1, 5		7, 5
Σ		16, 5

Получаем систему

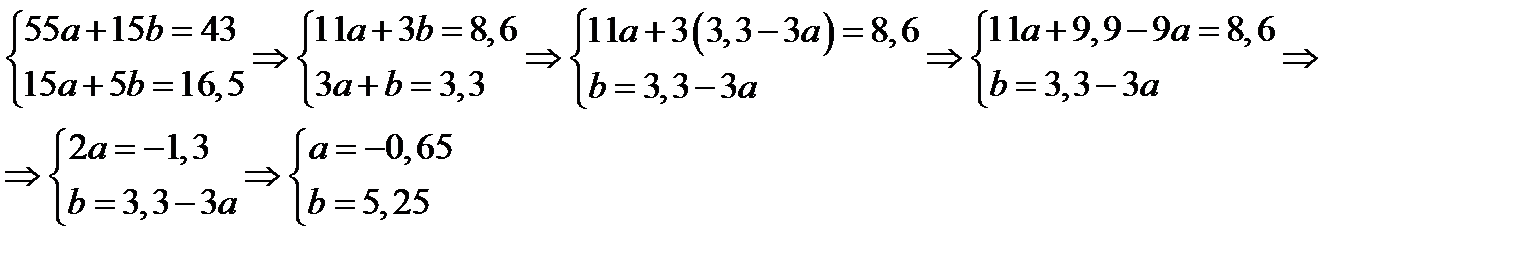
Уравнение искомой функции имеет вид .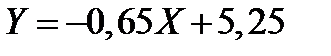

Построим график

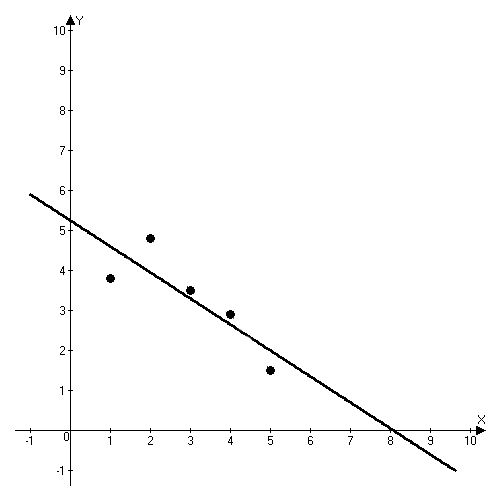
Задача 15. Экспериментально получены пять значений функции 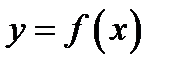, которые записаны в таблице. Методом наименьших квадратов найти функцию вида , аппроксимирующую функцию 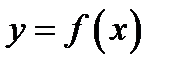. Сделать чертеж, на котором в декартовой прямоугольной системе координат изобразить экспериментальные точки и график аппроксимирующей функции.

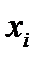
	4, 1	1, 7	1, 3	1, 2	0, 7

Решение:

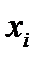
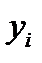
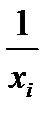
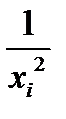
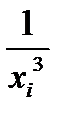
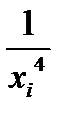
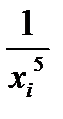
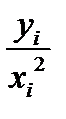
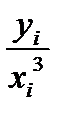
	1, 000	4, 100	1, 000	1, 000	1, 000	1, 000	1, 000	4, 100	4, 100
	2, 000	1, 700	0, 500	0, 250	0, 125	0, 063	0, 031	0, 425	0, 213
	3, 000	1, 300	0, 333	0, 111	0, 037	0, 012	0, 004	0, 144	0, 048
	4, 000	1, 200	0, 250	0, 063	0, 016	0, 004	0, 001	0, 075	0, 019
	5, 000	0, 700	0, 200	0, 040	0, 008	0, 002	0, 000	0, 028	0, 006
Σ	15, 000	9, 000	2, 283	1, 464	1, 186	1, 080	1, 037	4, 772	4, 385

Получаем систему

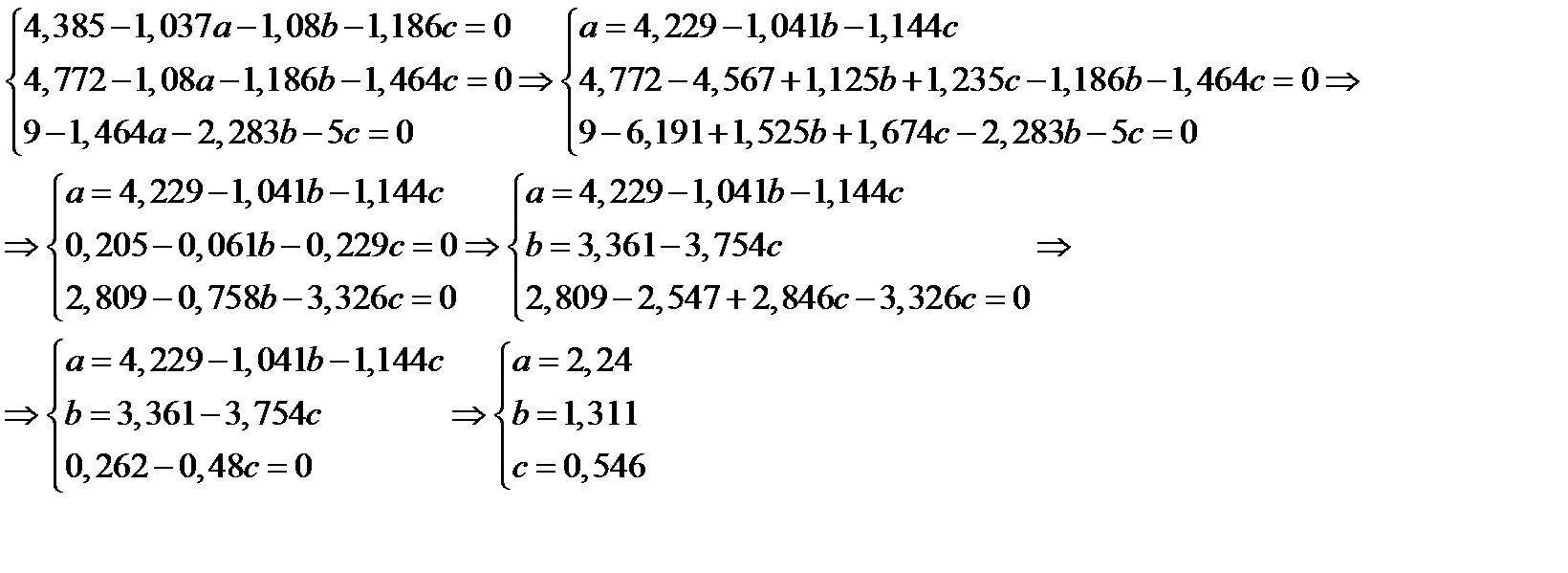
Искомая функция имеет вид:

Построим график

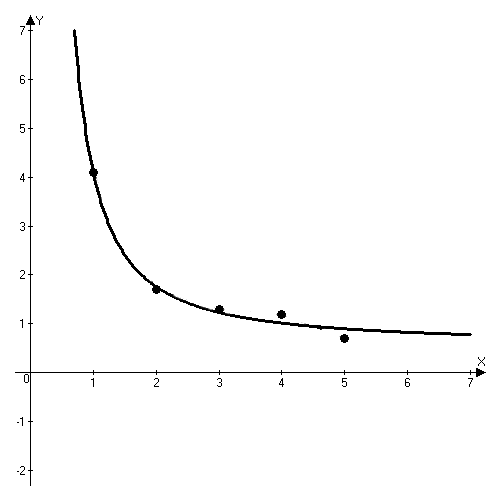
Задача 16. Найти прямоугольный параллелепипед наибольшего объема при условии, что длина его диагонали равна d.

Решение:

Необходимо найти максимум функции 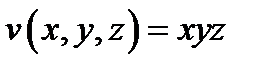. Известно, что 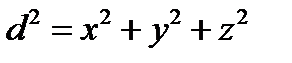, отсюда 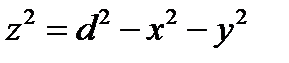. Так как максимум функции 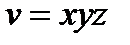будет достигаться там же где максимум функции 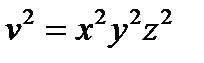, то нам необходимо найти максимум функции 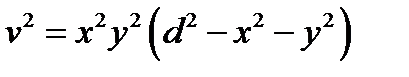. Составляем систему уравнений

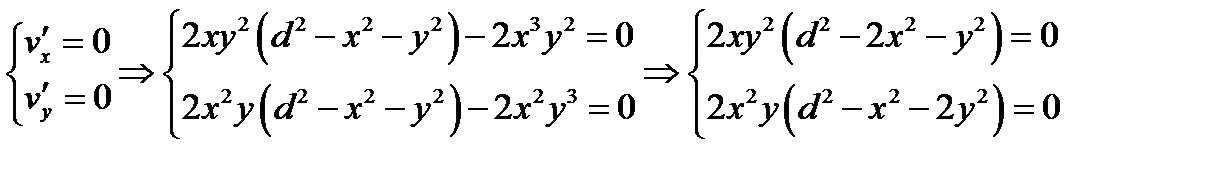
Так как 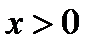и 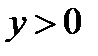, то имеем

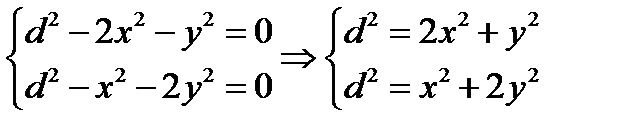
Значит

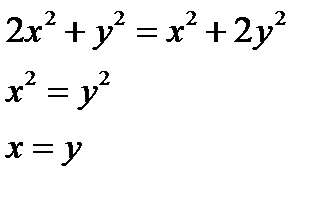
Из первого уравнения системы получаем 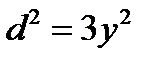или 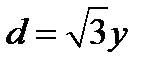, отсюда .

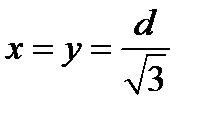Так как 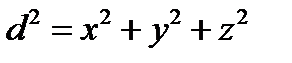, то .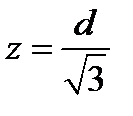

Прямоугольный параллелепипед с диагональю d будет иметь максимальный объем тогда, когда все его стороны будут равны 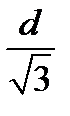, т.е. параллелепипед превратится в куб.