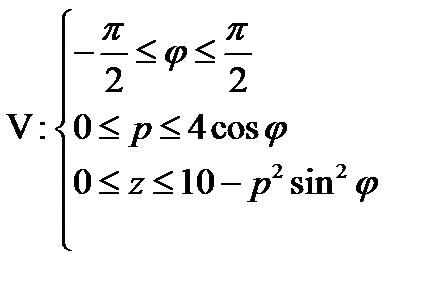Кратные интегралы

Задача 2. Вычислить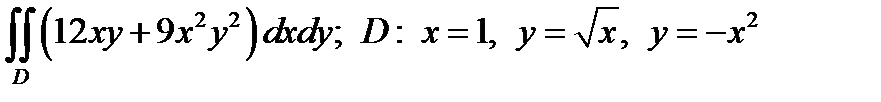

Решение:

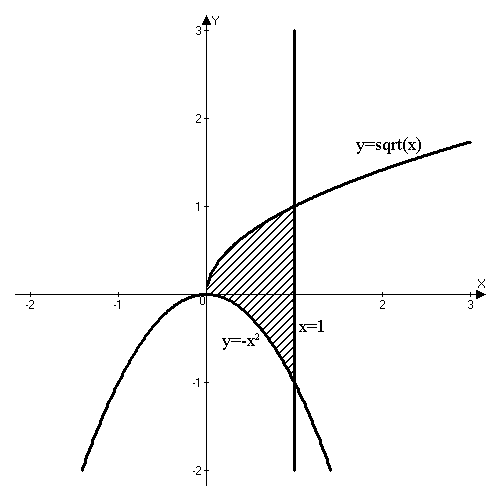
Изобразим область интегрирования

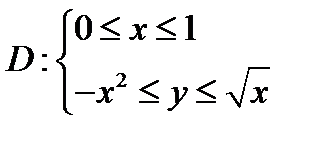
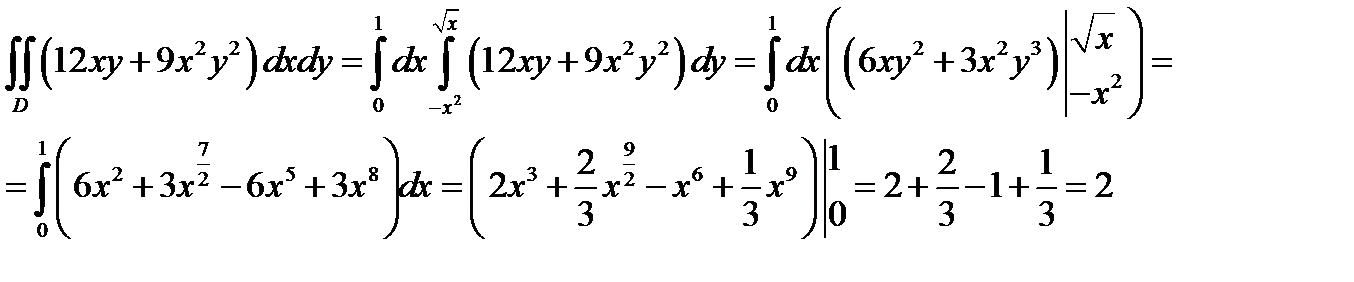
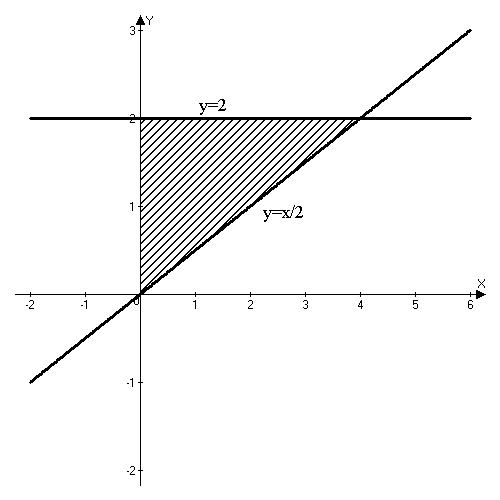
Задача 3. Вычислить

Решение:

Изобразим область интегрирования

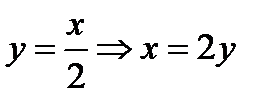
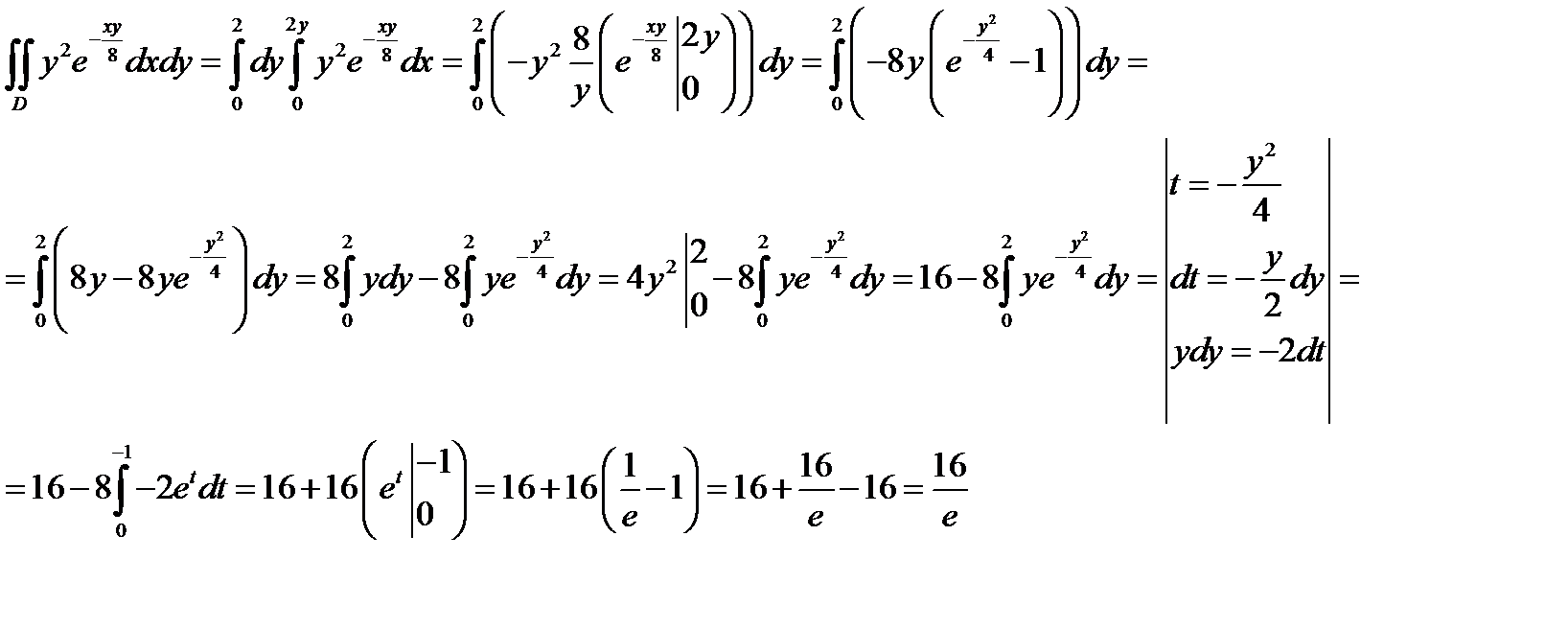
Задача 4. Вычислить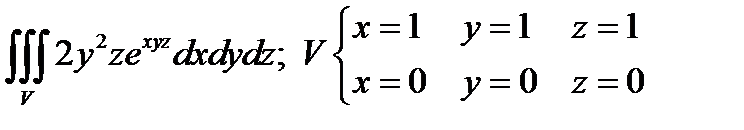

Решение:

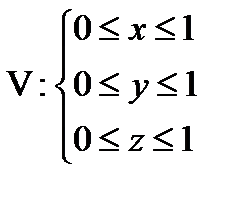
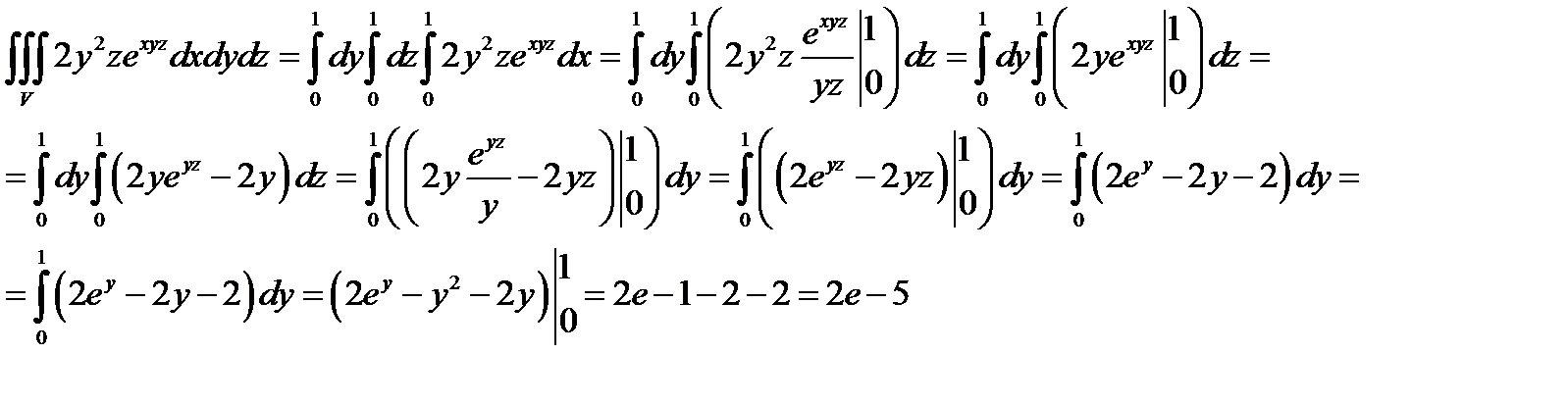
Задача 5. Вычислить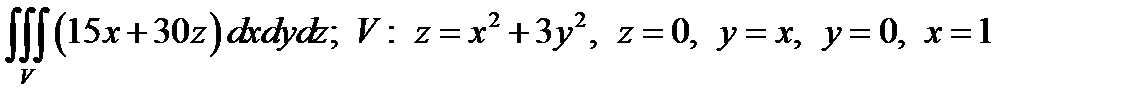

Решение:

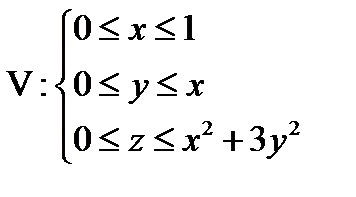
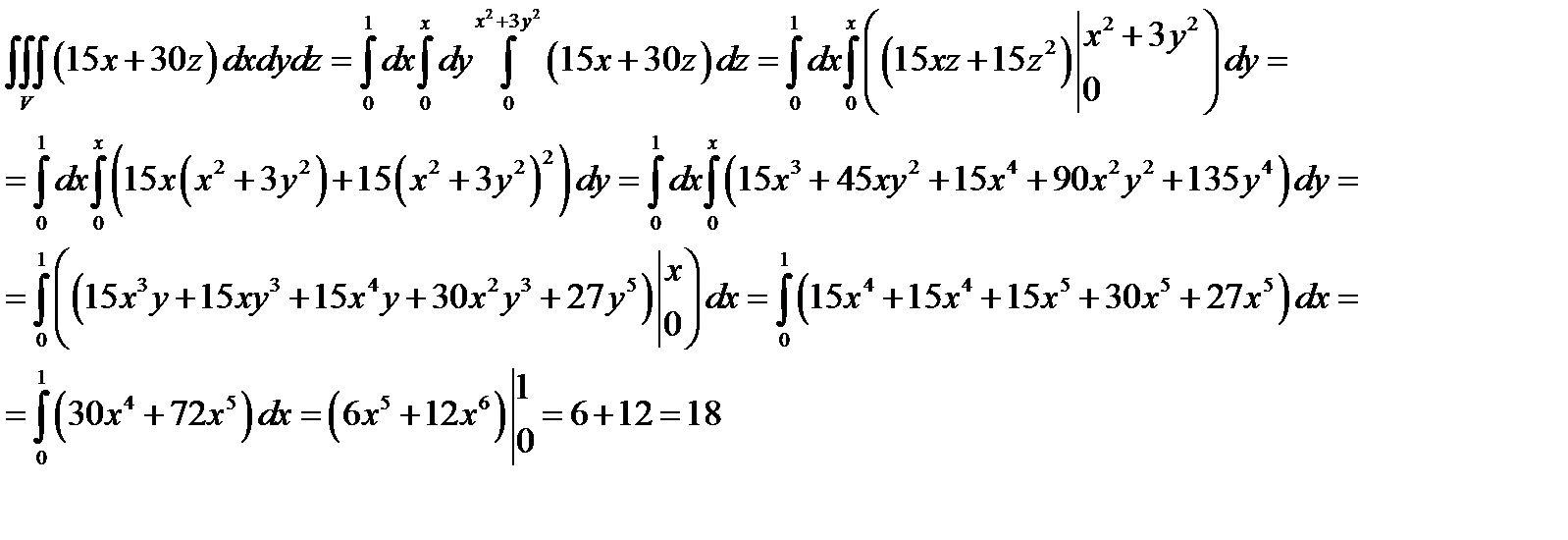
Задача 6. Найти площадь фигуры, ограниченной данными линиями .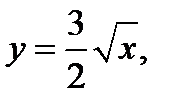

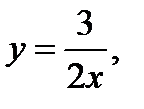
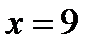Решение:

Изобразим область интегрирования

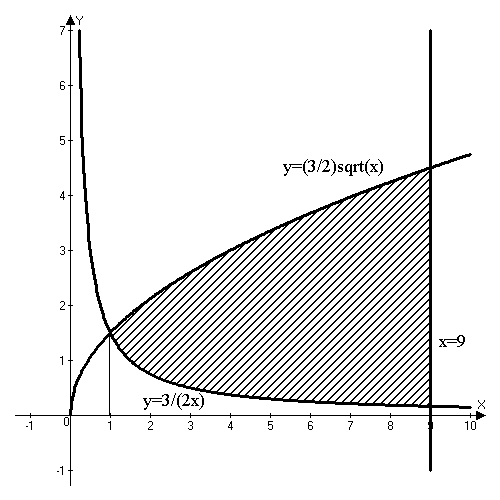
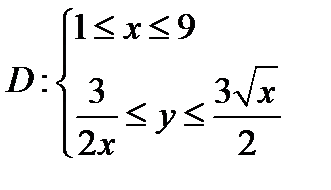
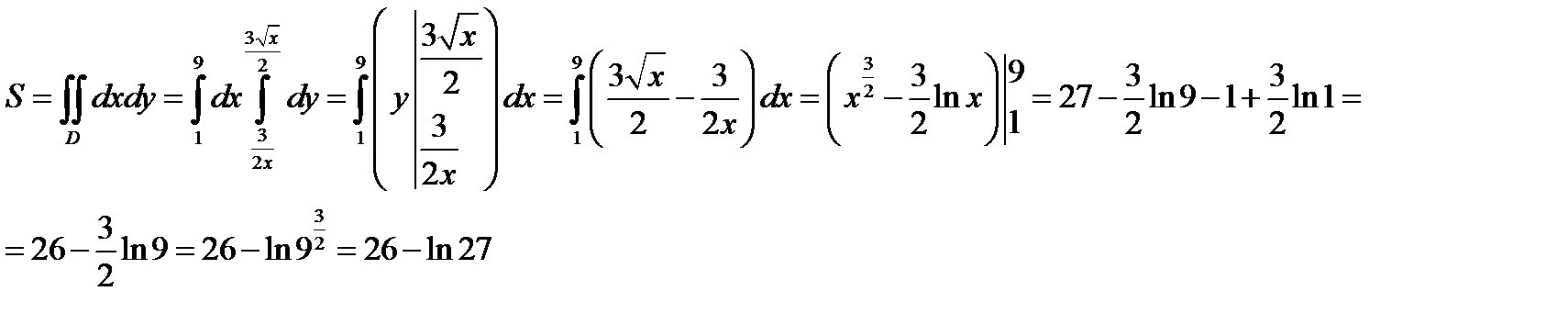
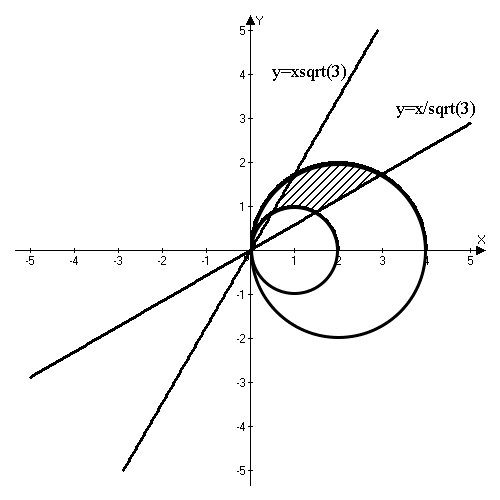
Задача 7. Найти площадь фигуры, ограниченной данными линиями , .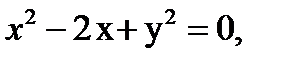

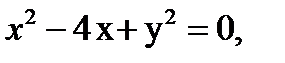
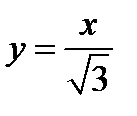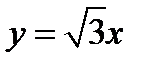Решение:

Определяем область интегрирования

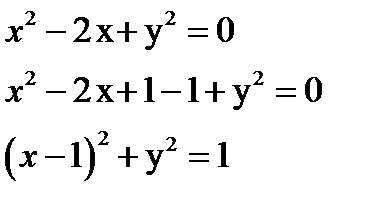
Таким образом, линия 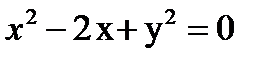- окружность с центром 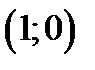и радиусом .

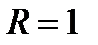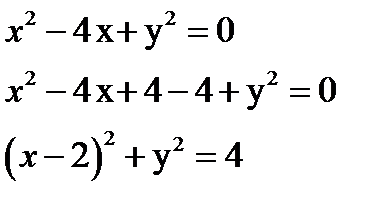
Таким образом, линия 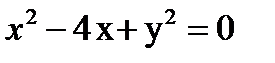- окружность с центром 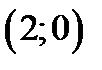и радиусом .

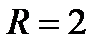Перейдем к полярным координатам 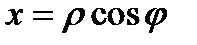, 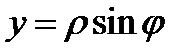. Уравнения примут вид

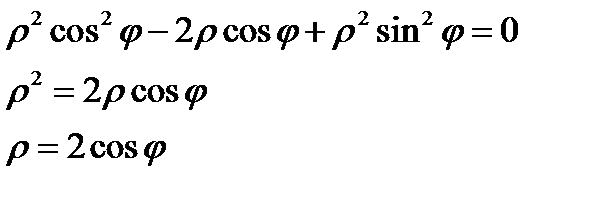
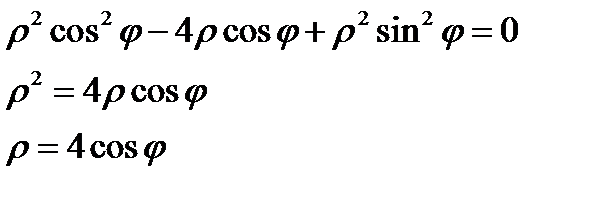
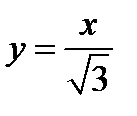, значит .

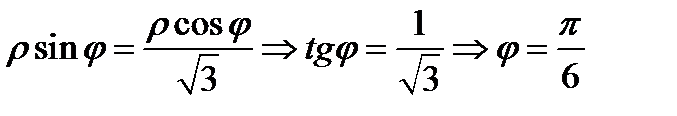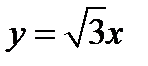, значит .

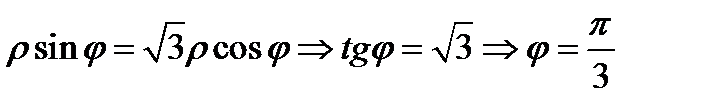Изобразим область интегрирования

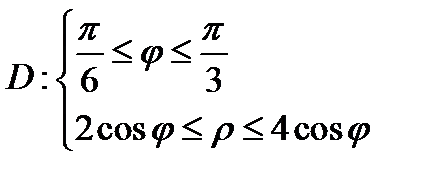
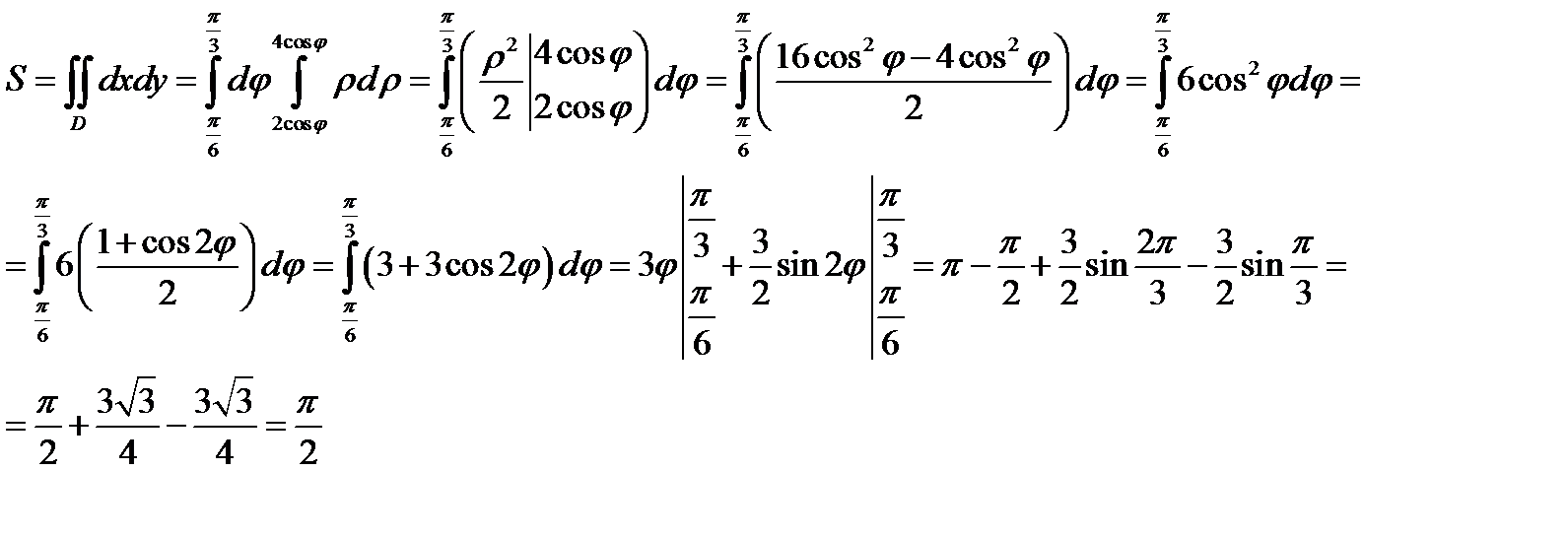
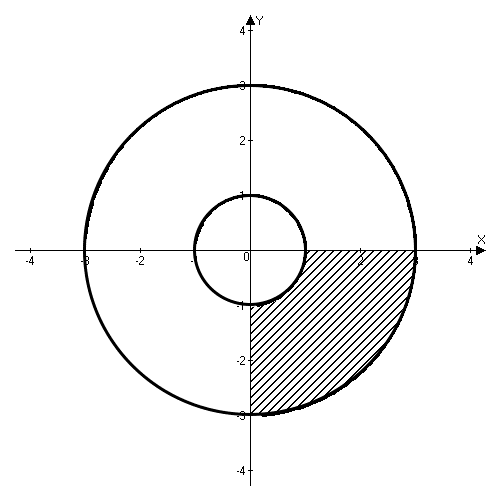
Задача 8. Пластинка D задана ограничивающими ее кривыми, µ - поверхностная плотность. Найти массу пластинки

;

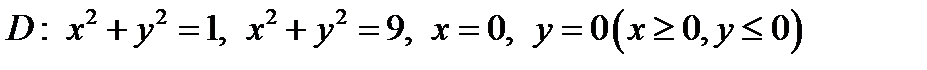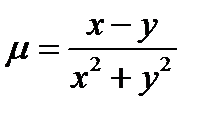
Решение:

Перейдем к полярным координатам , .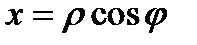

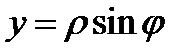Отсюда

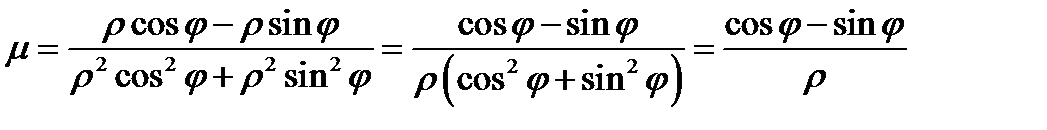
Изобразим область интегрирования

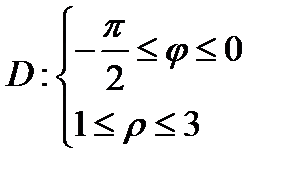
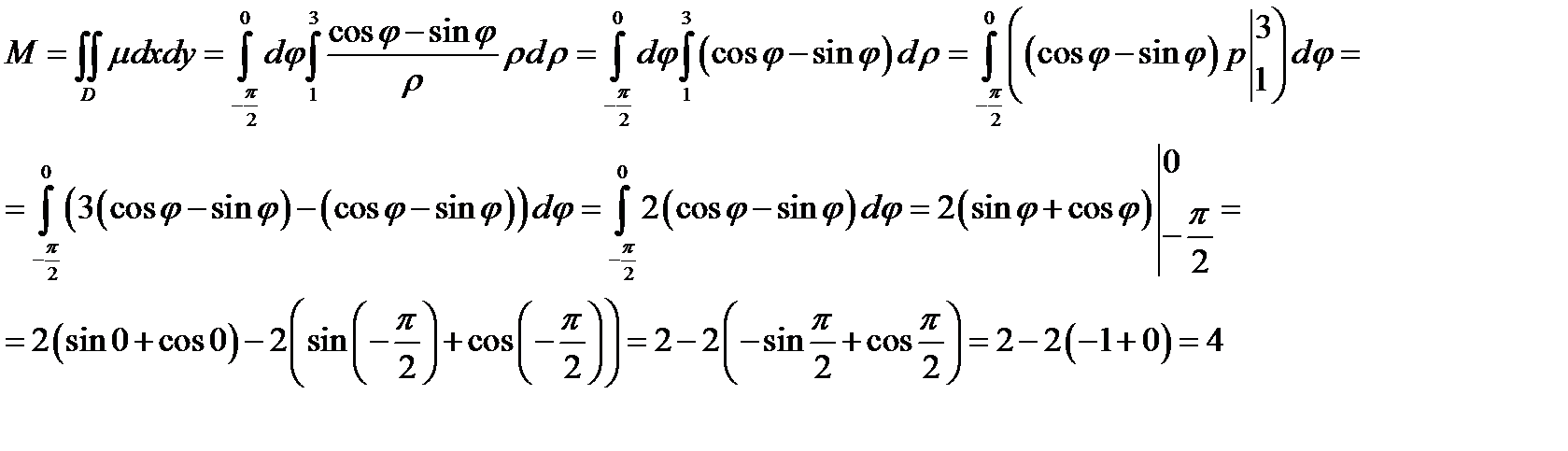
Задача 9. Пластинка D задана неравенствами, µ - поверхностная плотность. Найти массу пластинки

;

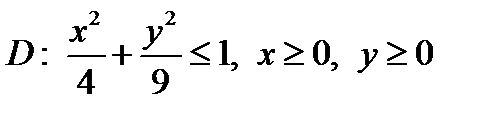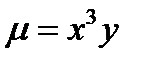
Решение:

Перейдем к полярным координатам , ,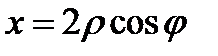

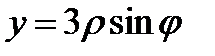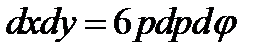
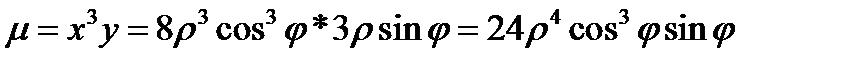
Изобразим область интегрирования

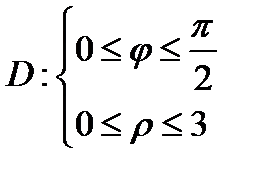
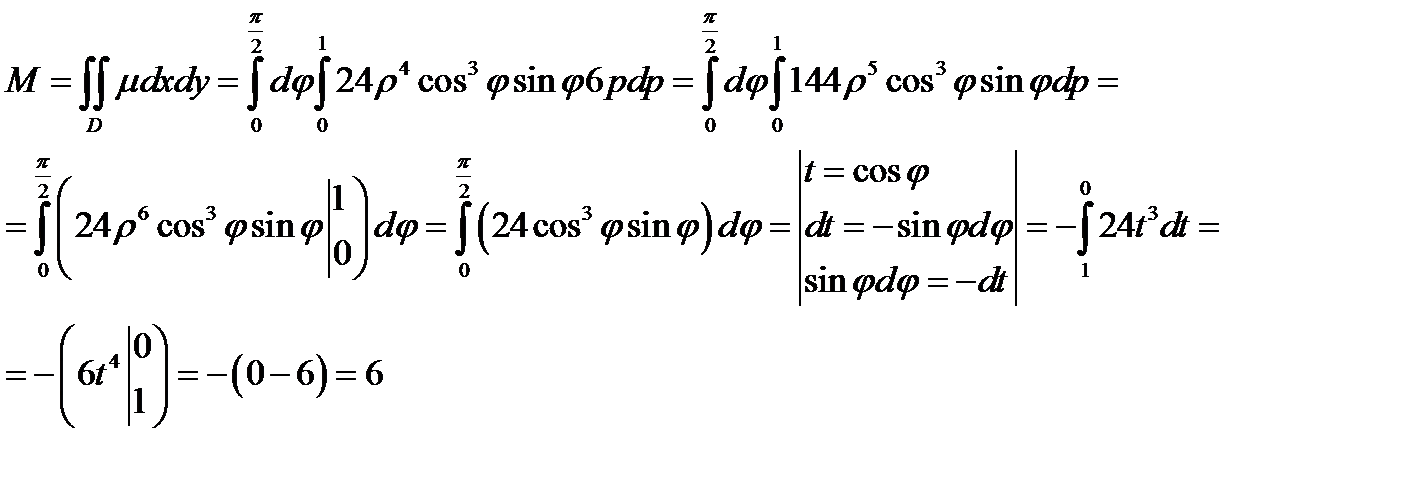
Задача 10. Найти объем тела, заданного ограничивающими его поверхностями

, , ,

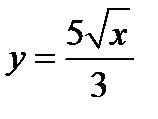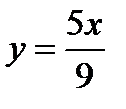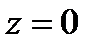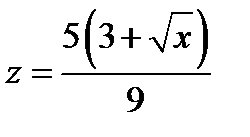
Решение:

Изобразим область интегрирования в плоскости XOY

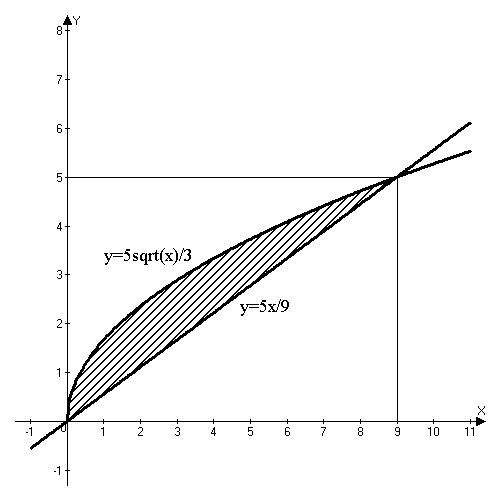
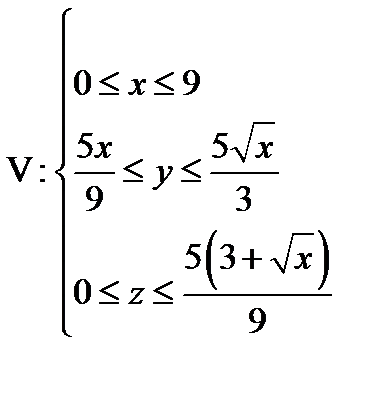
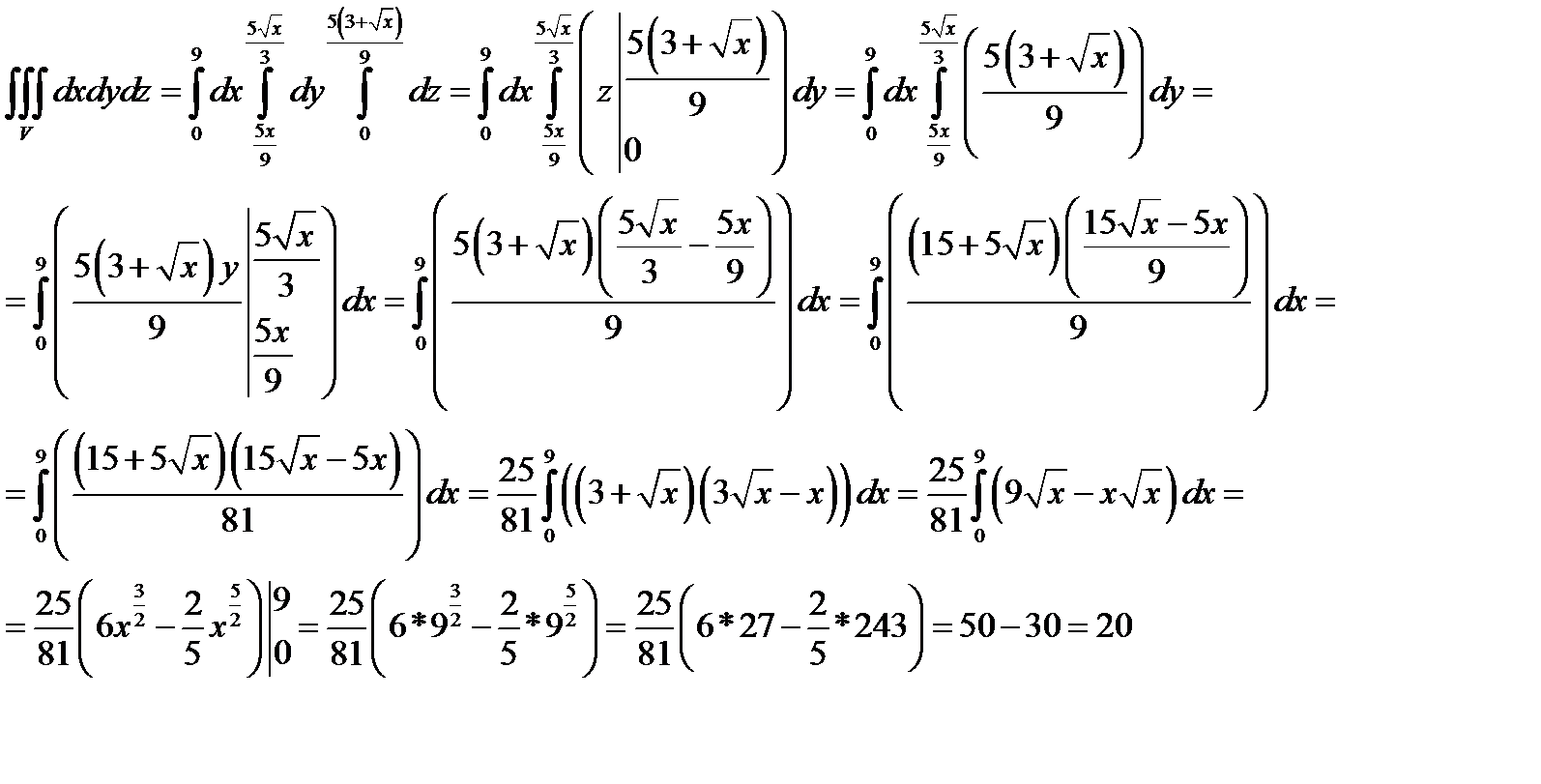
Задача 11. Найти объем тела, заданного ограничивающими его поверхностями

, ,

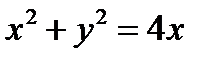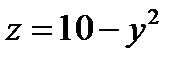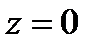
Решение:

Найдем область интегрирования

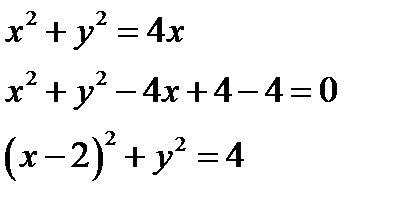
окружность радиуса 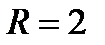и с центром в точке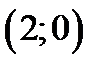

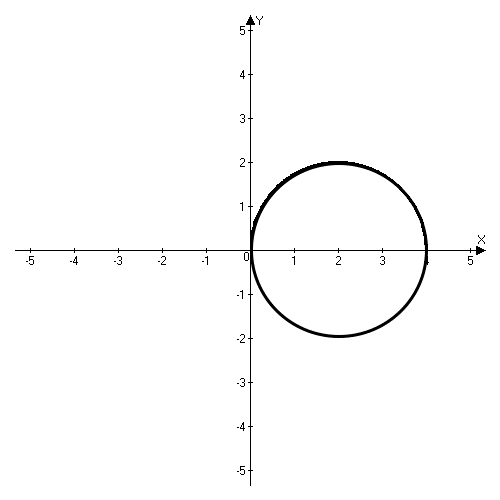
Перейдем к полярным координатам 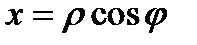, .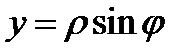