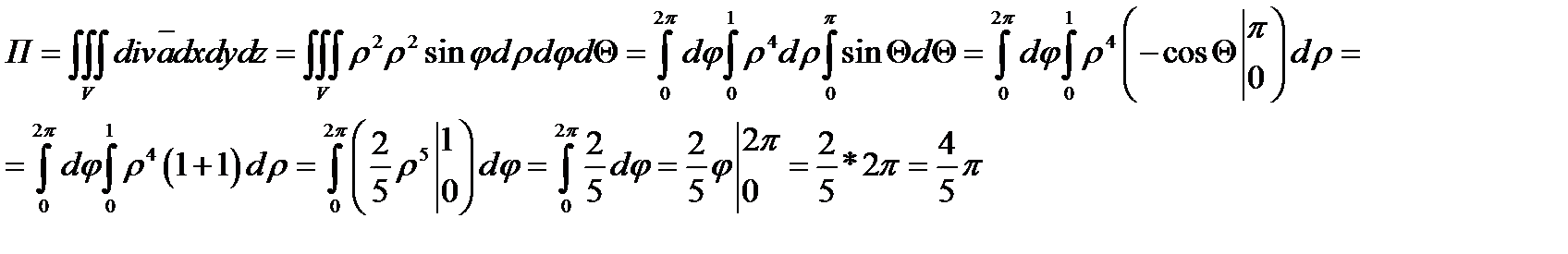Векторный анализ

Задача 1. Найти производную скалярного поля 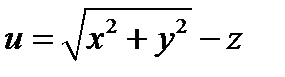в точке 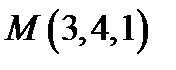по направлению проходящей через эту точку нормали к поверхности 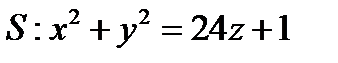, образующей острый угол с положительным направлением оси Oz.

Решение:

, ,

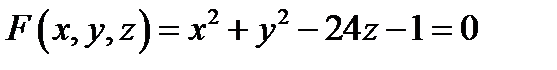
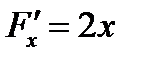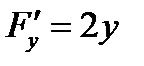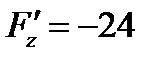
В точке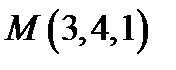

, ,

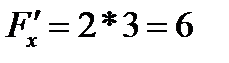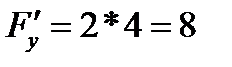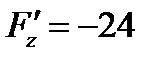
Отсюда нормальный вектор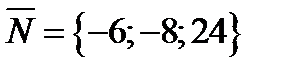

, ,

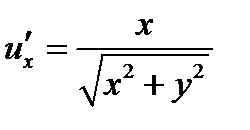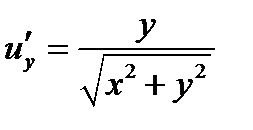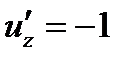
В точке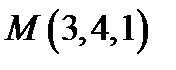

, ,

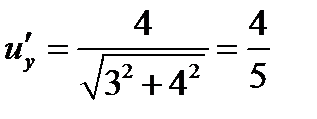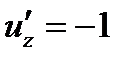
Отсюда градиент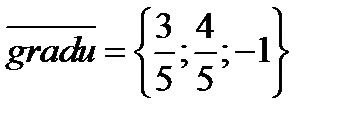

Производная скалярного поля по направлению

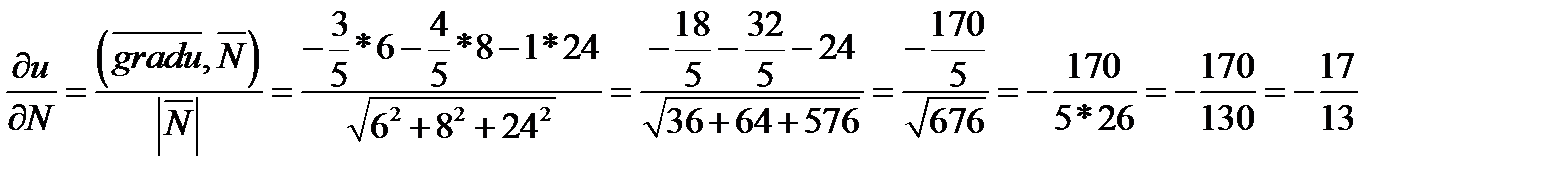
Задача 2. Найти угол между градиентами скалярных поле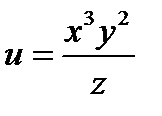й и 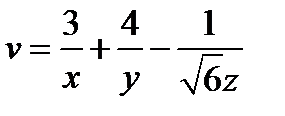в точке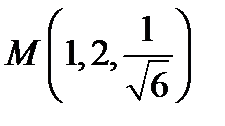

Решение:

, ,

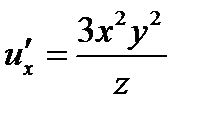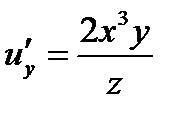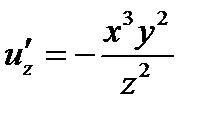
в точке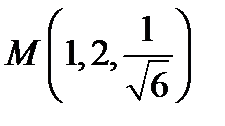

, ,

, ,

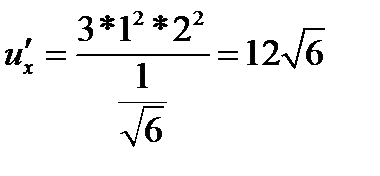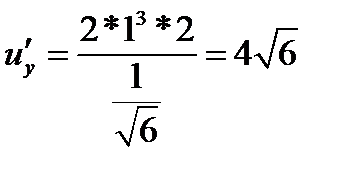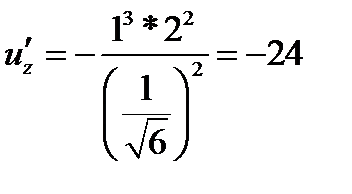
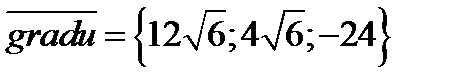
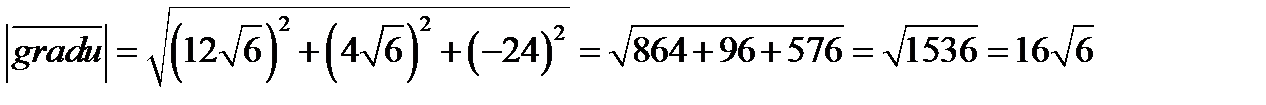
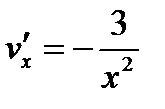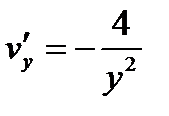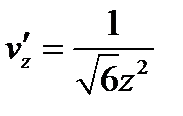
в точке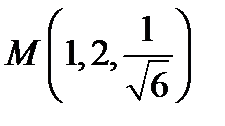

, ,

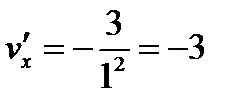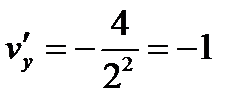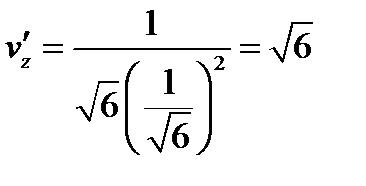
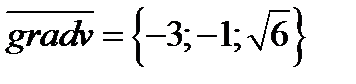
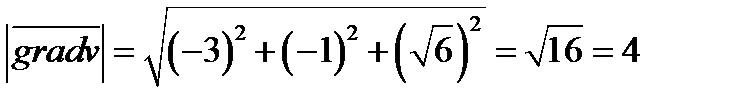
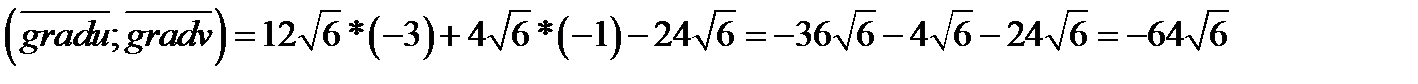
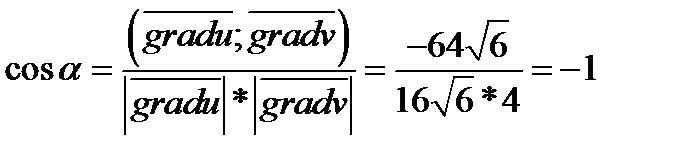
Таким образом угол между градиентами скалярных полей равен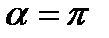

Задача 3. Найти векторные линии в векторном поле .

Решение:

, ,

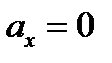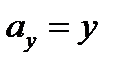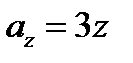
Уравнение векторной линии имеет вид 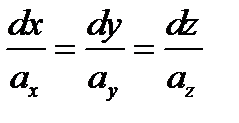или

Таким образом получаем систему

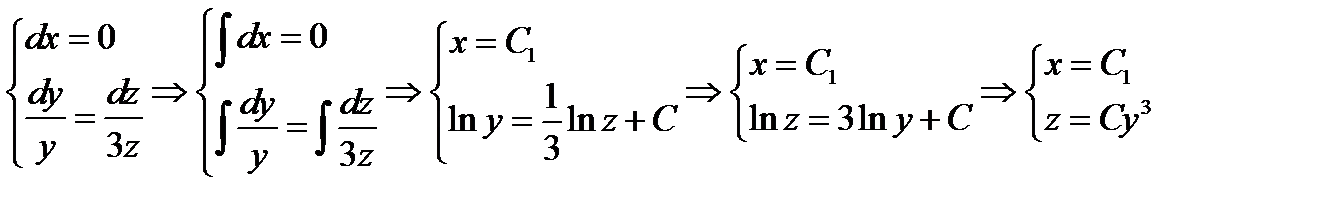
Векторные линии в векторном поле определяются уравнением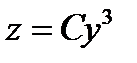

Задача 4. Найти поток векторного поля 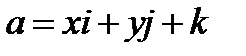через часть поверхности 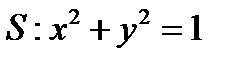, вырезаемую плоскостями , (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями)

Решение:

Данная поверхность, вырезаемая плоскостями , – прямой цилиндр с радиусом 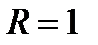и высотой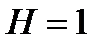

, ,

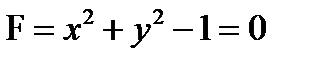
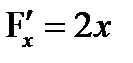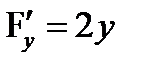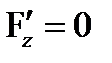
Отсюда нормальный вектор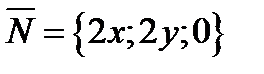

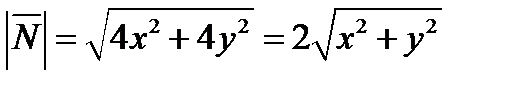
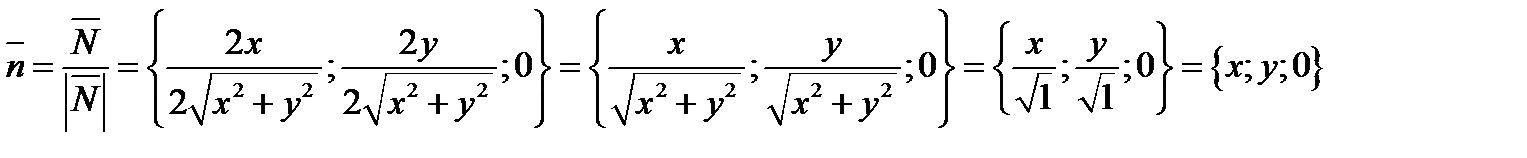
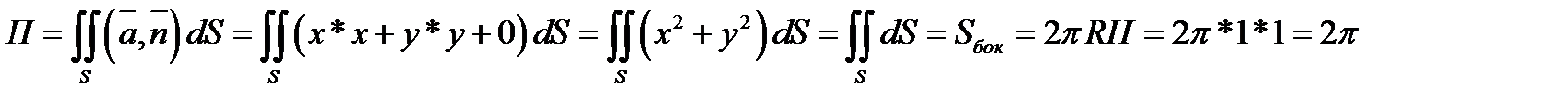
Задача 5. Найти поток векторного поля 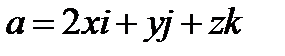через часть плоскости 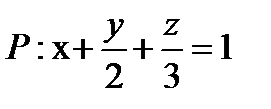, расположенную в первом октанте (нормаль образует острый угол с осью Oz)

Решение:

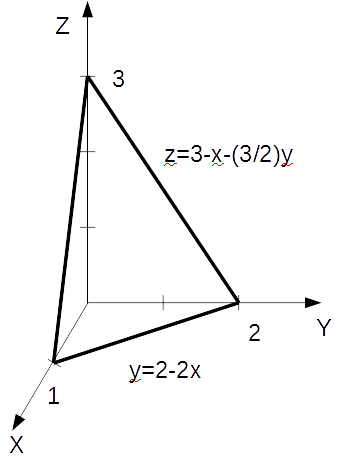
Находим дивергенцию

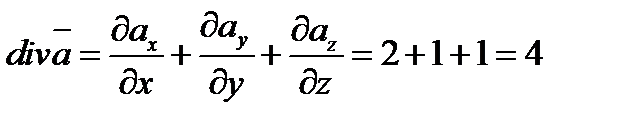
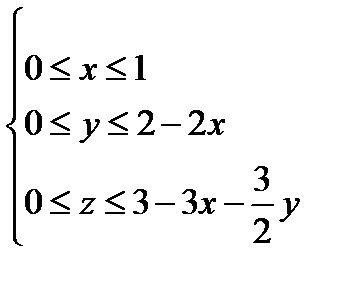
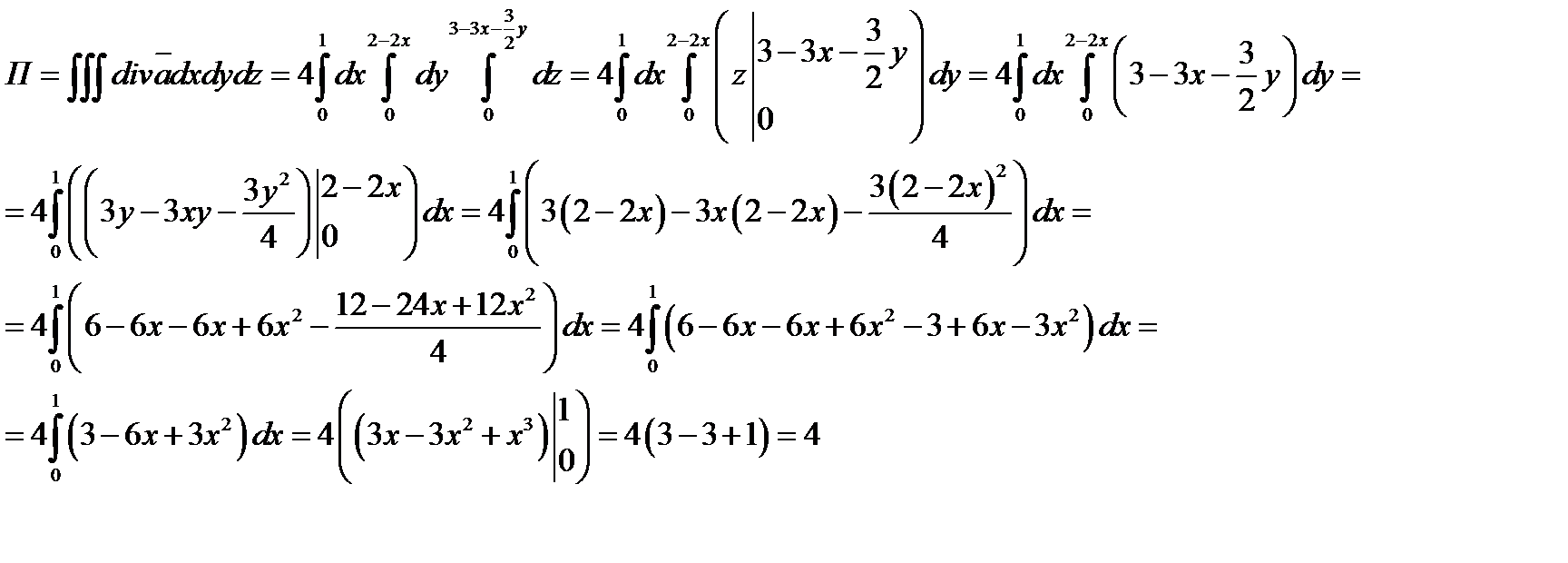
Задача 6. Найти поток векторного поля 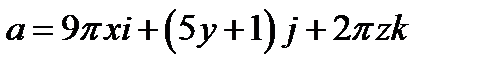через часть плоскости 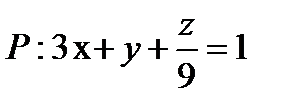, расположенную в I октанте (нормаль образует острый угол с осью Oz)

Решение:

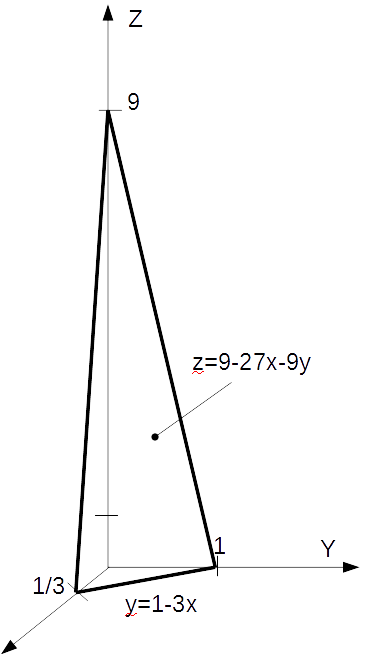
нормальный вектор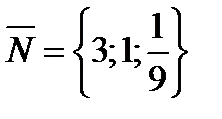

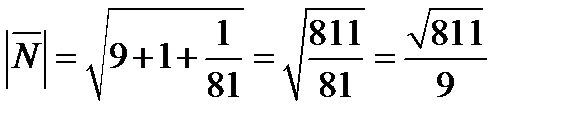
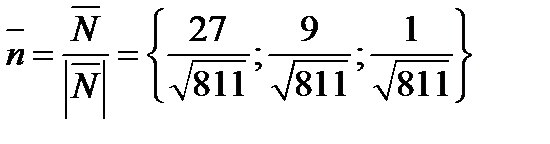
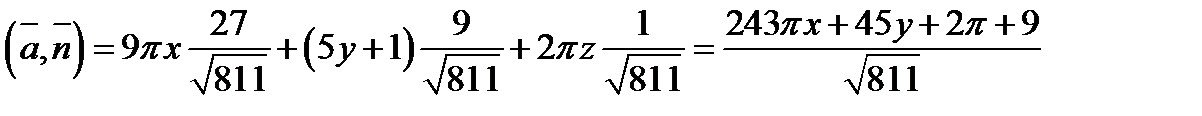
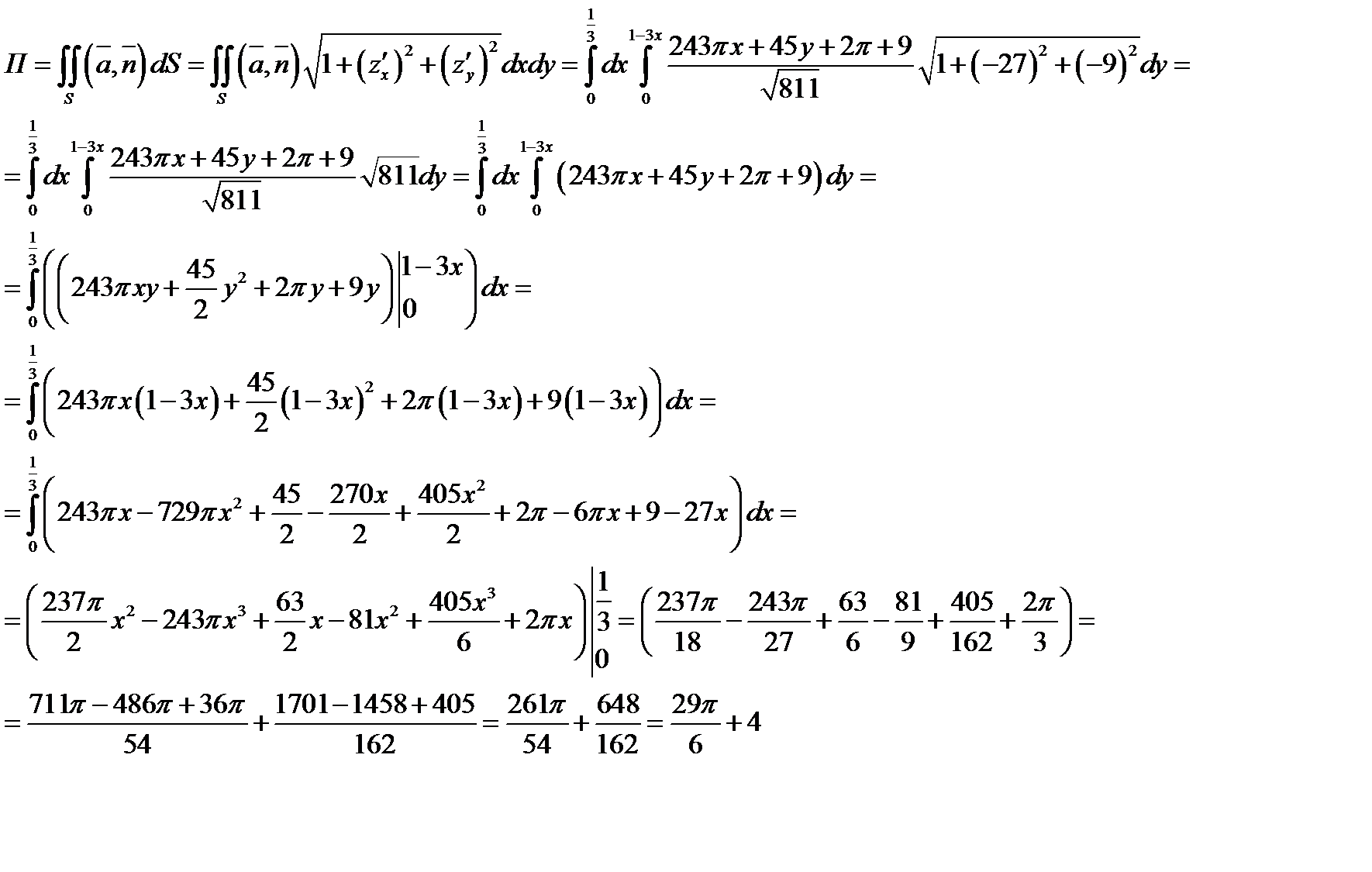
Задача 7. Найти поток векторного поля 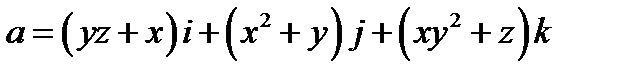через замкнутую поверхность 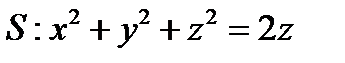(нормаль внешняя)

Решение:

Находим дивергенцию

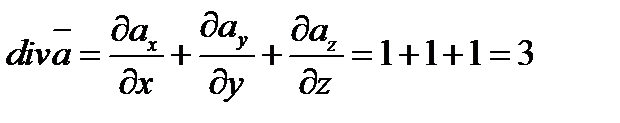
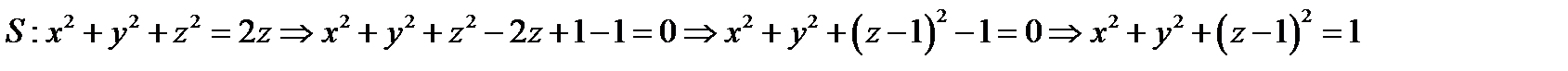Таким образом замкнутая поверхность является сферой с радиусом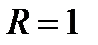

Определяем поток векторного поля через данную замкнутую поверхность

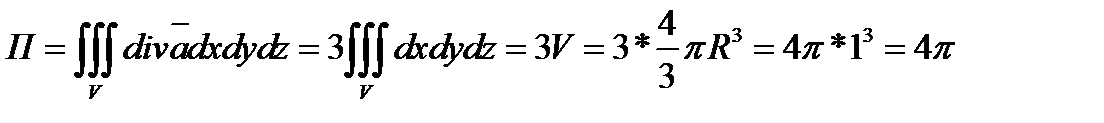
Задача 8. Найти поток векторного поля 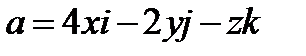через замкнутую поверхность 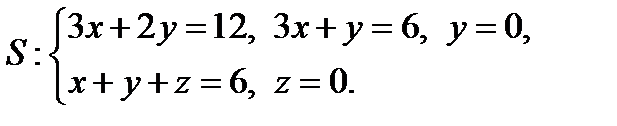(нормаль внешняя)

Решение:

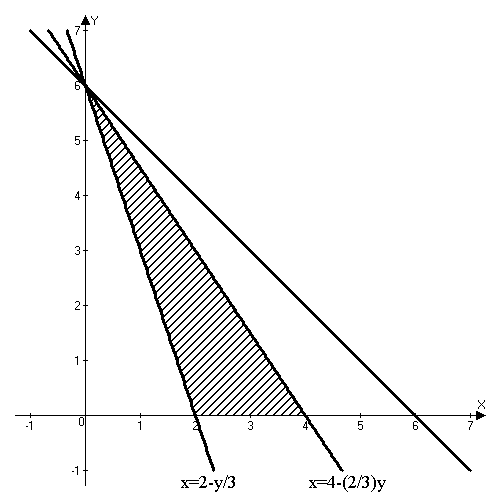
Находим дивергенцию

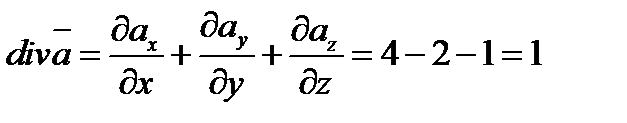
Определяем поток векторного поля через данную замкнутую поверхность

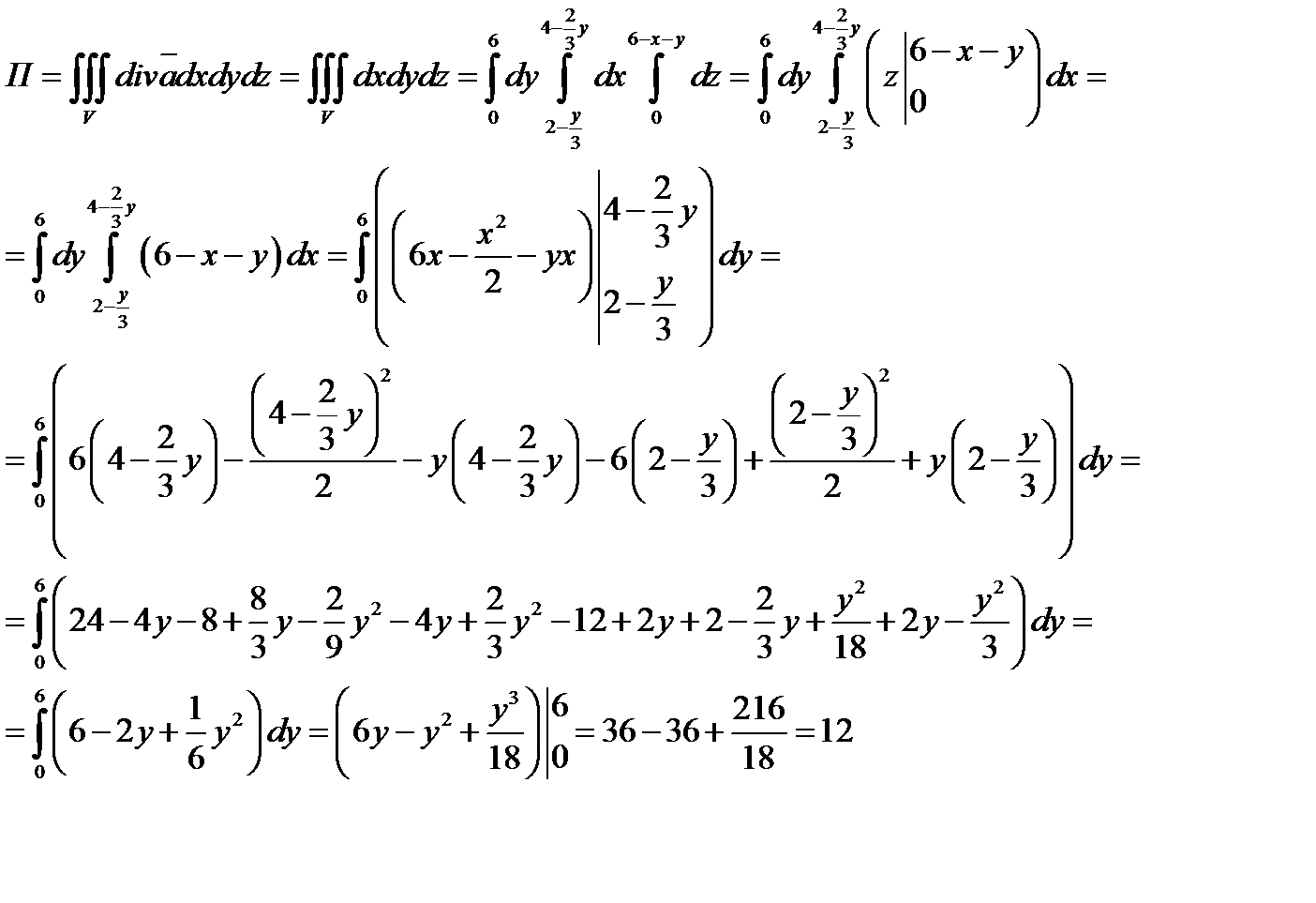
Задача 9. Найти поток векторного поля 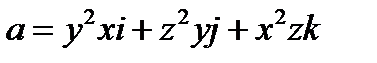через замкнутую поверхность 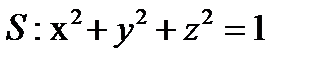(нормаль внешняя)

Решение:

Находим дивергенцию

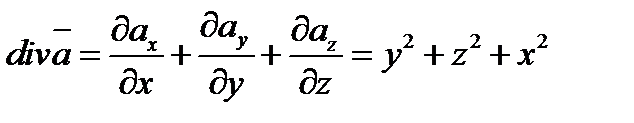
Замкнутая поверхность – сфера с центром в начале координат и радиусом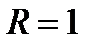

Определяем поток векторного поля через данную замкнутую поверхность

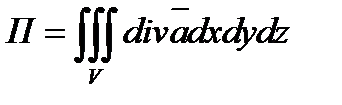
Переходим к сферическим координатам

Новые переменные изменяются в пределах

Таким образом