Синтез оптимального алгоритма управления

Составляем функцию Лагранжа:

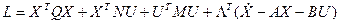
Записываем уравнения Эйлера-Лагранжа:

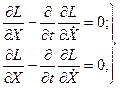(7)

Вычислим составленные соотношения:

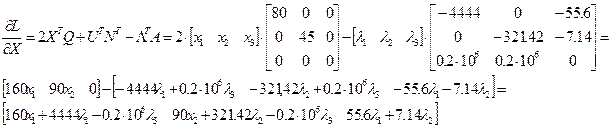
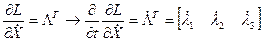
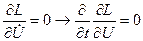
Тогда уравнения Эйлера-Лагранжа принимают вид:

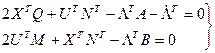(8)

К последним уравнениям добавляем уравнение связи (уравнение объекта), получаем следующую систему:

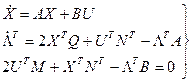(9)

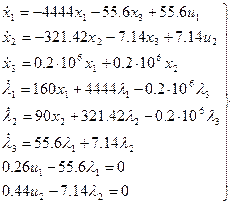(10)

Найдем U:

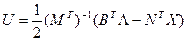
и подставим в первые три уравнения (10):

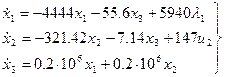(11)

Введем вектор 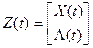. Тогда систему (10) с учетом (11) можно представить в виде:

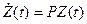(12)

где Р – блочная матрица, имеющая вид:

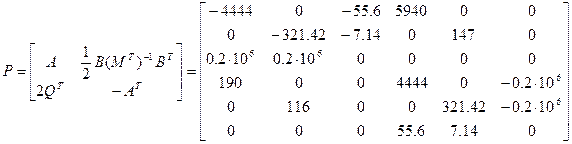(13)

Решение (12) в соответствии с формулой Коши:

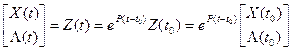(14)

Вычислив 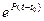, ее можно представить следующим образом:

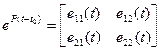(15)

где 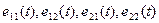- функциональные матрицы размеров .

Тогда из выражений (14), (15):

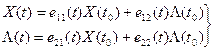(16)

Для определения начального значения множителя Лагранжа запишем следующие соотношения:

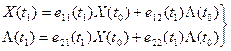(17)

Из первого уравнения (17) можно определить начальное условие множителя Лагранжа:

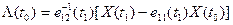
(18)

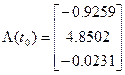
Теперь можно записать из выражений (16):

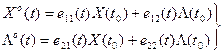(19)

Оптимальное управление определится выражением:

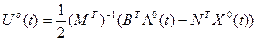
Таким образом найдены соотношения для оптимальной траектории и оптимального управления: